Эта плоскость будет перпендикулярна к плоскости проекций π2, поэтому она может быть задана как обычная проецирующая плоскость.
На рис. 3.5 б изображена плоскость β, с принадлежащем ей треугольником ABC, параллельная фронтальной плоскости проекций. Такую плоскость мы будем называть фронтальной.
Самостоятельно!
1.Профильно - проецирующая плоскость.
2.Профильная плоскость уровня
3.2.Особые линии плоскости.
Кособым линиям плоскости относятся линии уровня, т.е. прямые, принадлежащие данной
плоскости, одновременно, параллельные одной из плоскостей проекций.
Рис.3.6
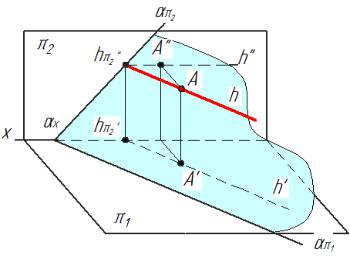
На рис. 3.6 дано наглядное изображение горизонтали h , принадлежащей плоскости α и
параллельной плоскости проекций π1, на рис. 3.7 - эпюр этой прямой.
.
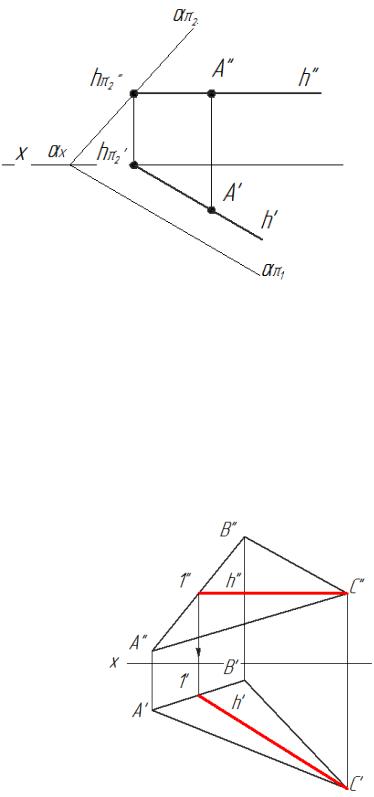
Рис.3.7
Прямая h называется горизонталью плоскости α. В любой плоскости можно провести множество горизонталей. Все они будут параллельны между собой.
Горизонтальный след απ1 плоскости α тоже является горизонталью плоскости α. Следовательно: h║απ1 → (h′ ║απ1) ^ (h″ ║х).
Рис.3.8
На рис. 3.8 построена горизонталь h плоскости α (∆АВС).
29
а) |
б) |
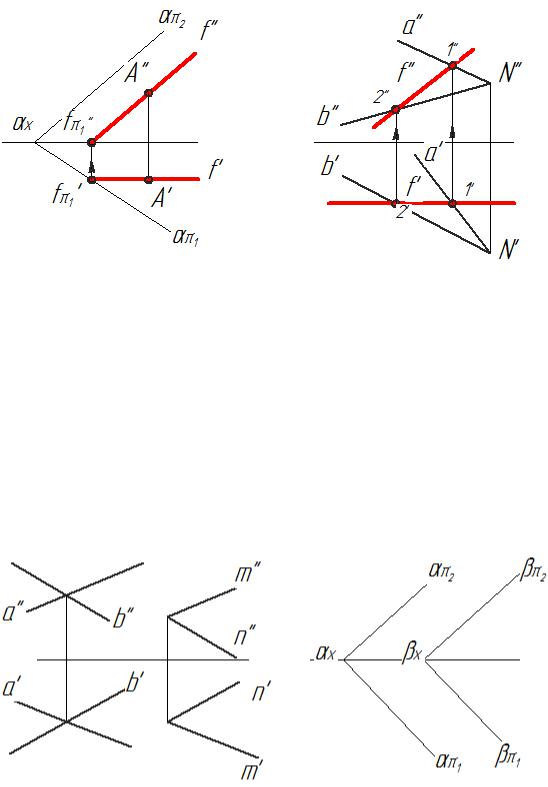
Рис.3.9 На рис. 3.9 приведено изображение фронтали плоскости α заданной следами (рис.3.9, а) и
пересекающимися прямыми а и в (рис. 3.9, б).
3.3.Параллельность плоскостей.
Если плоскости параллельны, то двум пересекающимся прямым одной плоскости
соответственно параллельны две пересекающиеся прямые другой плоскости.
а) |
б) |
Рис. 3.10
Плоскости α (a∩b) и β (m∩n) (рис. 3.10, а) параллельны между собой, т.к. прямая а параллельна прямой m, а прямая b параллельна прямой n.
Если плоскости заданы следами (рис. 3.10 б), то определение параллельности плоскостей будет выглядеть так.
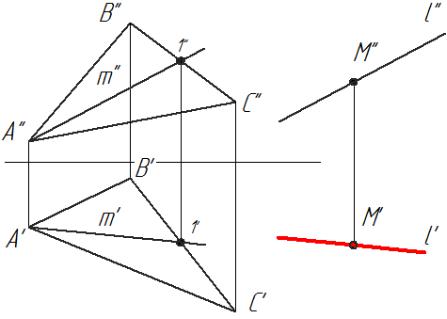
Если плоскости параллельны, то их одноименные следы будут также параллельны.
3.4.Прямая, параллельная плоскости.
Прямая будет параллельна плоскости в том случае, если в плоскости найдется прямая,
параллельная данной.
Задача.
Дана точка М и фронтальная проекция прямой ℓ, проходящей через эту точку. Построить горизонтальную проекцию прямой ℓ, зная, что эта прямая параллельназаданнойплоскости α(∆ABC) (рис. 3.11).
Рис. 3.11
Строим в плоскости треугольника прямую m, параллельную прямой ℓ и находим направление горизонтальной проекции прямой ℓ.
3.5.Взаимное пересечение двух плоскостей.
В зависимости от расположения пересекающихся плоскостей относительно плоскостей проекций
возможны следующие задачи:
1.Обе пересекающие плоскости - одноименно проецирующие.
2.Пересекающиеся плоскости - разноименно проецирующие.
3.Одна из пересекающихся плоскостей - плоскость общего положения, другая - проецирующая.
31
4. Обе пересекающиеся плоскости - плоскости общего положения.
3.5.1. Построение линии пересечения двух плоскостей, если одна из пересекающихся плоскостей - плоскость общего положения, другая - проецирующая.
Рис.3.12 |
Рис.3.13 |
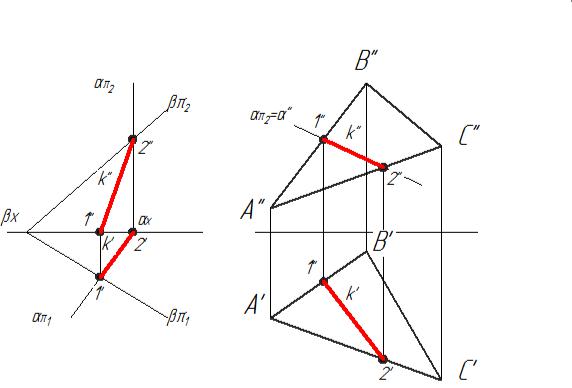
На рис. 3.12 горизонтально - проецирующая плоскость α(απ1, απ2) и плоскость общего положения β (βπ1, βπ2) пересекаются по прямой k.
На рис. 3.13 пересекаются фронтально - проецирующая плоскость α(απ2, α") и плоскость общего положения β(∆АВС).
В обоих случаях одна из проекций линии пересечения определяется сразу из условия принадлежности проецирующей плоскости, другая - плоскости общего положения. Задача относится к разряду простых. При решении большого круга позиционных задач часто применяются вспомогательные секущие плоскости, в качестве которых, как правило, используют проецирующие плоскости.
3.5.2. Построение линии пересечения двух плоскостей, если обе пересекающиеся плоскости - плоскости общего положения.
Поскольку линией пересечения двух плоскостей является прямая, то для ее построения необходимо найти положение какихлибо двух точек этой прямой.
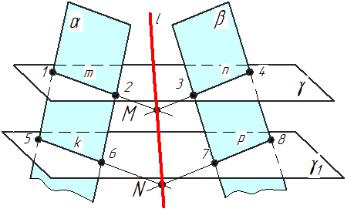
На рис.3.14 показано построение линии пересечения плоскостей α и β.
Алгоритм решения:
1.Ввести вспомогательную секущую плоскость γ.
2.Построить линию пересечения плоскости γ с каждой из плоскостей:
m = α∩γ; n = β∩γ;
3. Найти точку пересечения найденных линий: M = m∩n;
Используя приведенный алгоритм решения найти втору точку линии пересечения:
k = α ∩ γ1; p = β ∩ γ1; N = k∩ p;
Рис.3.14
На рис.3.15 показано построение линии пересечения плоскостей α(a ∩ b) и β(сlld) на комплексном чертеже. γ,γ1 – фронтально – проецирующие плоскости.
33
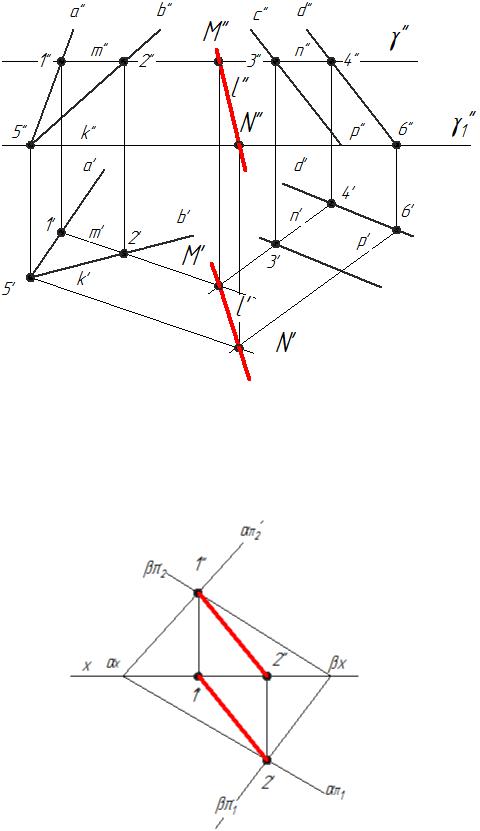
Рис.3.15
На рис.3.16 показано построение линии пересечения плоскостей общего положения α(απ1, απ2)
и β(βπ1, βπ2).
Рис.3.16