
chap_0
.pdf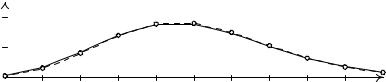
11.6. РОЗПОДIЛ ПIРСОНА |
123 |
p
0:2
0:1
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
x |
Рис. 11.13. Зв’язок бiномного та пуассонiвського розподiлiв
11.6Розподiл Пiрсона
Нехай U1, U2,. . . , Un – незалежнi нормально розподiленi нормованi випадковi величини. Розглянемо суму квадратiв цих величин
2 = U2 |
+ U2 |
+ : : : + U2 |
: |
(11.16) |
1 |
2 |
n |
|
|
Випадкова величина 2 має розподiл, щiльнiсть якого задається
формулою |
8 |
|
|
|
|
|
x 0; |
|
kn(x) = |
0; |
1 |
|
(11.17) |
||||
|
|
|
|
xn2 1e x2 ; x > 0: |
||||
|
|
|
n |
(n2 ) |
|
|||
|
< |
2 |
2 |
|
|
|||
:
Розподiл, заданий щiльнiстю kn(x), називається розподiлом Пiрсона або 2-розподiлом. Параметр n визначає число ступенiв вiльностi розподiлу, а (a) – гамма-функцiя Ейлера. Зокрема, (1) = 1, (2) = 1, (n) = (n 1)! (n = 3; 4; : : :).
Розподiл Пiрсона Kn(x) = R1x kn(t) dt визначає ймовiрнiсть настання подiї 2 < x, iншими словами, заданому числу x ставить у вiдповiднiсть ймовiрнiсть за формулою = Kn(x). Обернена функцiя Kn 1( ), навпаки, заданiй ймовiрностi ставить у вiдповiднiсть число x. Таблиця Е.4 на с.248 мiстить значення такої оберненої функцiї.
Функцiї kn(x), Kn(x) та Kn 1( ) у рiзних пiдручниках, монографiях та програмних продуктах можуть позначатись порiзному. Так у програмному продуктi Mathcad вони позначаються вiдповiдно так: dchisg(x; n), pchisg(x; n) та qchisg( ; n). Приклад. Розподiл Пiрсона pchisg(15; 987; 10) = 0; 9. Обернений розподiл Пiрсона qchisg(0; 9; 10) = 15; 987.

124 |
РОЗДIЛ 11. ОСНОВНI ЗАКОНИ РОЗПОДIЛУ |
p
0:2
0:1
0 |
5 |
10 |
15 |
x |
Рис. 11.14. Пiрсона розподiл
Основнi параметри 2(n)-розподiлу :
Математичне очiкування m = M[ 2(n)] = n;
Дисперсiя d = D[ 2(n)] = 2n;
p
Середнє квадратичне вiдхилення = 2n.
При n 2 функцiя щiльностi постiйно спадає для x > 0, а при n > 2 має єдиний максимум у точцi x = n 2. Графiки функцiї щiльностi для деяких значень n зображенi на рис. 11.14.
Розподiл 2(n) для великих n (n > 30) можна апроксимувати нормальним розподiлом iз математичним очiкуванням n i дисперсiєю 2n. Тому, для великих n користуються нормальним розподiлом. Рис. 11.15 iлюструє таку апроксимацiю.
Розподiл 2 вiдiграє важливу роль у математичнiй статистицi. Як приклад, можна послатися на формулу (14.8) с. 171, де з допомогою такого розподiлу розв’язуються задачi дисперсiйного аналiзу.
11.7Розподiл Стьюдента
Нехай U, U1, U2,. . . , Un незалежнi нормально розподiленi нормованi випадковi величини. Розглянемо нову випадкову величину
|
|
|
U |
(11.18) |
||
t = |
|
|
|
|
: |
|
|
|
|
|
|||
|
pU12 |
+ U22 |
+ : : : + Un2 |
|
||
11.7. РОЗПОДIЛ СТЬЮДЕНТА |
125 |
p
0:05
0:025
10 |
20 |
30 |
40 |
50 x |
Рис. 11.15. Зв’язок розподiлiв Пiрсона та нормального
Розподiлом такої величини є розподiл Стьюдента або t-розподiл, щiльнiсть якого задається формулою
s |
|
(x) = |
1 |
|
(n+12 ) |
(1 + |
x2 |
) n+12 |
: |
(11.19) |
|
|
|
|
|
|
|
||||||
|
n |
|
pn |
|
(n2 ) |
|
n |
|
|||
Параметр n визначає число ступенiв вiльностi цього розподiлу.
Основнi параметри розподiлу Стьюдента:
Математичне очiкування m = M[t] = 0;
Дисперсiя d = D[t] = nn 2 ;
q
Середнє квадратичне вiдхилення = nn 2 .
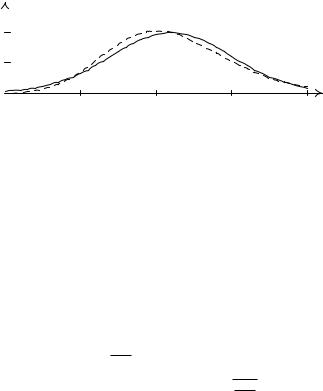
Функцiя щiльностi sn(x) симетрична вiдносно точки x = 0 i має єдиний максимум в цiй точцi. Графiк функцiї sn(x) зображений на рис. 11.16, де для порiвняння штриховою лiнiєю зображений ще й графiк нормального розподiлу.
Iнтегральна функцiя
Z x
Sn(x) = sn(u) du
1
дає змогу обчислити ймовiрнiсть попадання значень випадкової величини x у промiжок (1; x). Обернена функцiя Sn 1( ), навпаки, заданiй ймовiрностi ставить у вiдповiднiсть число x. На-
приклад, S11( 1; 796) = 0; 05; S111(0; 05) = 1; 796. Таблиця Е.3 на с.246 мiстить значення такої оберненої функцiї.

126 |
РОЗДIЛ 11. ОСНОВНI ЗАКОНИ РОЗПОДIЛУ |
|
p |
|
0:3 |
|
0:2 |
|
0:1 |
|
4 3 2 1 0 1 2 3 4 x |
|
Рис. 11.16. Щiльность розподiлу Стьюдента |
Значення функцiй Sn 1( ), Sn 1(1 ) рiвнi за модулем, але протилежнi за знаком. Тому S111(0; 95) = 1; 796. Зазначимо, що ймовiрнiсть прийняти випадковою величиною x значення, що перевищує число Sn 1( ), дорiвнює 1 .
Функцiї sn(x), Sn(x) та Sn 1( ) у рiзних джерелах можуть позначатись по-рiзному. Так у програмному продуктi Mathcad вони позначаються вiдповiдно так: dt(x; n), pt(x; n) та qt( ; n).
Розподiл Стьюдента для великих n можна апроксимувати стандартизованим нормальним розподiлом. Для невеликих значень n розподiл Стьюдента помiтно вiдрiзняється вiд нормального, що iлюструє рис. 11.16. Ймовiрнiсть вiдхилень вiд нуля (середнього значення) бiльша для розподiлу Стьюдента нiж для нормального розподiлу.
Розподiл Стьюдента широко використовується при математичнiй обробцi результатiв вимiрювань (с.151), перевiрцi гiпотез (с.162, с.167) тощо.
11.8Розподiл Фiшера
Щiльнiсть розподiлу Фiшера або F -розподiлу задається формулою
|
(n+2m ) |
|
n |
n2 |
|
|
xn2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
(11.20) |
|
|
(n2 ) (m2 ) |
m |
(mn x + 1) |
2 |
|
|||||
fnm(x) = |
|
|
|
|
|
|
n+m x: |
|||

11.9. КОНТРОЛЬНI ПИТАННЯ |
127 |
p
0:75
0:5 

0:25 

0 |
1 |
2 |
3 |
4 x |
Рис. 11.17. Розподiл Фiшера
Бачимо, що розподiл залежить вiд двох параметрiв m та n, якi називаються ступенями вiльностi. На основi щiльностi будується розподiл Фiшера: Fnm(x) = R0x fnm(t) dt. На рис. 11.17 показанi два графiки функцiї щiльностi.
Якщо деяка випадкова величина пiдлягає розподiлу Фiшера, то функцiя Fnm(x) визначає ймовiрнiсть настання подiї < x, iншими словами, заданому числу x ставить у вiдповiднiсть ймо-
вiрность за формулою = Fnm(x). Обернена функцiя Fnm1( ), навпаки, заданiй ймовiрностi ставить у вiдповiднiсть число x.
Таблицi Е.5 та Е.6 на с.250 мiстять значення оберненої функцiї.
Функцiї fnm(x), Fnm(x) та Fnm1( ) у програмному продуктi Mathcad позначаються вiдповiдно: dF (x; n; m), pF (x; n; m) та
qF ( ; n; m).
Розподiл Фiшера застосовується при розв’язаннi важливих задач дисперсiйного аналiзу (див. приклад на c. 173).
11.9Контрольнi питання
1.Опишiть значення нормального закону для розв’язання рiзноманiтних практичних задач.
2.Яка функцiя щiльностi для нормального закону?
3.Як знайти математичне очiкування та дисперсiю для нормального закону?
4.Розкрийте змiст правила трьох сигм.
5.Дайте означення рiвномiрного розподiлу.
128 |
РОЗДIЛ 11. ОСНОВНI ЗАКОНИ РОЗПОДIЛУ |
6.Яка щiльнiсть розподiлу, математичне очiкування та дисперсiя рiвномiрного закону?
7.Опишiть практичнi задачi, де застосовується рiвномiрний закон?
8.Дайте означення бiномного розподiлу.
9.Яка щiльнiсть розподiлу, математичне очiкування та дисперсiя бiномного закону?
10.Опишiть практичнi задачi, де застосовується бiномний закон?
11.Який закон розподiлу називається показниковим?
12.Охарактеризуйте параметри показникового розподiлу.
13.Що таке функцiя надiйностi? Наведiть приклади її застосування.
14.Дайте характеристику розподiлу Пуассона.
15.Чому закон Пуассона часто називають законом рiдкiсних явищ?
16.Який зв’язок бiномного та пуассонiвського розподiлiв?
17.Дайте означення розподiлу Пiрсона.
18.Назвiть прикладнi задачi, де використовується розподiл Пiрсона.
19.Який зв’язок мiж розподiлами Пiрсона та нормальним?
20.Дайте означення розподiлу Стьюдента.
21.Опишiть роль розподiлу Стьюдента при математичнiй обробцi результатiв вимiрюиань.
22.Який зв’язок мiж розподiлами Стьюдента та нормальним?
23.Дайте означення розподiлу Фiшера.
24.Опишiть роль розподiлу Стьюдента при розв’язаннi важливих задач дисперсiйного аналiзу.
11.10Задачi роздiлу
11.1. Проводиться зважування деякої речовини без систематичних похибок. Випадковi похибки зважування задовольняють нормальному закону iз середнiм квадратичним вiдхиленням = 20 г. Знайти ймовiрнiсть того, що зважування буде проведене з похибкою, яка не перевищує за абсолютною величиною 10 г.

11.10. ЗАДАЧI РОЗДIЛУ |
129 |
Розв’язування. Математичне очiкування випадкових помилок дорiвнює нулю, тому можна застосувати формулу
p(jxj < ) = 2 ( = ):
Покладемо = 10, = 20, тодi p(jxj < 10) = 2 (0; 5). За таблицею Е.2 на с. 244 знаходимо (0; 5) = 0; 1915. Отже, шукана ймовiрнiсть p(jxj < 10) = 0; 3830.
11.2. Математичне очiкування нормально розподiленої випадкової величини x дорiвнює m = 3, середнє квадратичне вiдхилення= 2. Написати щiльнiсть розподiлу x. Знайти ймовiрнiсть того, що значення випадкової величини попаде в промiжок (1; 4).
|
|
e |
(x 3)2 |
|
Вiдповiдь. f(x) = |
2p12 |
8 |
; p = 0; 5328. |
|
11.3. Автомат штампує деталi. Контролюється довжина деталi x, яка розподiлена нормально з математичним очiкуванням (проектна довжина), рiвним 50 мм. Фактично довжина виготовлених деталей не менше 32 та не бiльше 68 мм. Знайти ймовiрнiсть того, що довжина деталi, яка узята навмання: а) бiльше 55 мм; б) менше 40 мм.
Вiдповiдь. а) 0,0823; б) 0,0027. З рiвностi p(32 < x < 68) = 1 попередньо знайти .
11.4. Випадковi похибки вимiрювання задовольняють нормальному закону з середнiм квадратичним вiдхиленням = 20 мм та математичним очiкуванням a = 0. Знайти ймовiрнiсть того, що в трьох незалежних вимiрюваннях похибка принаймнi одного вимiрювання не перевищить за абсолютною величиною 4 мм.
Вiдповiдь. p = 0; 41.
11.5. Випадкова величина x розподiлена нормально з математичним очiкуванням a = 10. Ймовiрнiсть попадання значення x в iнтервал (10; 20) дорiвнює 0,3. Чому дорiвнює ймовiрнiсть попадання значення x в iнтервал (0; 10)?
Вiдповiдь. p = 0; 3.
11.6. Випадкова величина x розподiлена нормально з математичним очiкуванням a = 25. Ймовiрнiсть попадання x в iнтервал (10; 15) дорiвнює 0,2. Знайти ймовiрнiсть попадання значення x в iнтервал (35; 40).
Вiдповiдь. p = 0; 2.
130 |
РОЗДIЛ 11. ОСНОВНI ЗАКОНИ РОЗПОДIЛУ |
11.7. Вага риби, яку вирощують у ставку, задовольняє нормальному закону з математичним очiкуванням m = 375 г та середнiм квадратичним вiдхиленням = 25 г. Знайти ймовiрнiсть того, що вага однiєї уловленої риби буде: а) знаходитись у межах вiд 300 г до 425 г; б) не бiльше 450 г; в) не менше 400 г.
Вiдповiдь. а) 0,976; б) 0,999; в) 0,16.
11.8. Випадкова величина x пiдпорядкована нормальному законовi з математичним очiкуванням m = 10. Яким повинно бути середнє квадратичне вiдхилення , щоб з ймовiрнiстю 0,8 модуль вiдхилення x вiд m не перевищував 0,2?
Вiдповiдь. 0,156.
11.9. Вважається, що вiдхилення довжини деталей вiд стандарту розподiлене нормально з параметрами m = 40 см i = 0; 4 см. Яку точнiсть довжини виробу можна гарантувати з ймовiрнiстю 0,8?
Вiдповiдь. 0,52.
11.10. Стрiльба ведеться з точки 0 вздовж променя Ох. Дальнiсть польоту розподiлена нормально iз середнiм квадратичним вiдхиленням = 80 м. Який вiдсоток випущених снарядiв дасть перелiт вiд 120 до 160 м?
Вiдповiдь. 4,4.
11.11. Випадкова величина x пiдпорядкована нормальному законовi з математичним очiкуванням m = 1; 6 i середнiм квадратичним вiдхиленням = 1. Яка ймовiрнiсть, що при 4-ох випробуваннях значення x хоча б один раз попаде в iнтервал (1; 2)?
Вiдповiдь. 0,8533.
11.12. Випадкова величина x пiдпорядкована нормальному законовi з математичним очiкуванням m = 2; 2 i середнiм квадратичним вiдхиленням = 0; 5. Яка ймовiрнiсть того, що при першому випробуваннi значення x знаходитиметься на вiдрiзку [3; 4], а при другому випробуваннi – на вiдрiзку [1; 2]?
Вiдповiдь. 0,018.
11.13. Цiна подiлки шкали амперметра дорiвнює 0,1 А. Показання закруглюють до найближчої подiлки. Знайти ймовiрнiсть того, що при вiдлiку буде зроблена похибка, яка перевищує 0,02 А.
11.10. ЗАДАЧI РОЗДIЛУ |
131 |
Обчислити математичне очiкування та дисперсiю похибки вимiрювання як випадкової величини.
Вiдповiдь. p = 0; 6; m = 0; 05; d = 8; 3 10 4.
11.14. Автобуси деякого маршруту йдуть строго за розкладом. Iнтервал руху – 5 хвилин. Знайти ймовiрнiсть того, що пасажир, який пiдiйшов до зупинки, буде чекати чергового автобусу менше 3 хвилин. Обчислити математичне очiкування та дисперсiю часу чекання як випадкової величини.
Вiдповiдь. p = 0; 6; m = 2; 5; d = 2; 083.
11.15. Хвилинна стрiлка електричного годинника рухається стрибком наприкiнцi кожної хвилини. Знайти ймовiрнiсть того, що в дану мить годинник покаже час, який вiдрiзняється вiд справжнього не бiльше нiж на 20 секунд. Обчислити математичне очiкування та дисперсiю похибки часу за електричним годинником як випадкової величини.
Вiдповiдь. p = 2=3; m = 30; d = 300.
11.16. Всi значення рiвномiрно розподiленої величини лежать на вiдрiзку [2; 8]. Знайти ймовiрнiсть попадання значення цiєї величини в iнтервал (3; 5).
Вiдповiдь. 1=3.
11.17. Трамваї деякого маршруту йдуть з iнтервалом в 5 хв. Пасажир приходить на зупинку в деякий момент часу. Яка ймовiрнiсть, що вiн прийде пiзнiше нiж одна хвилина пiсля вiдправлення попереднього поїзда, але ранiше нiж 2 хв. до прибуття наступного поїзда?
Вiдповiдь. 2=5.
11.18. Тривалiсть роботи елемента має показниковий розподiл F (t) = 1 e 0;02t (t > 0). Знайти ймовiрнiсть, що за 24 години елемент: 1) вiдмовить 2) не вiдмовить.
Вiдповiдь. F (24) = 0; 3812; R(24) = 0; 6188.
11.19. Час безвiдмовної роботи телевiзора розподiлений згiдно щiльностi показникового розподiлу R(t) = 0; 002e 0;02t (t > 0). Знайти ймовiрнiсть того, що телевiзор пропрацює 1000 год.
Вiдповiдь. R(1000) = e 2 = 0; 1359.
132 |
РОЗДIЛ 11. ОСНОВНI ЗАКОНИ РОЗПОДIЛУ |
11.20.Тривалiсть роботи електронної лампи є випадкова величина x, яка має показниковий розподiл iз параметром = 0; 003. Через рiк лампу замiнюють, якщо навiть вона i не вийшла з ладу. Знайти математичне очiкування часу роботи лампи.
11.21.Система складається з n блокiв. Нехай ti – час безвiдмовної роботи i-го блоку. Випадковi величини t1,. . . , tn – незалежнi i мають показниковий розподiл iз параметром . Система виходить iз ладу, якщо перестає працювати принаймнi один iз блокiв. Знайти функцiю розподiлу часу безвiдмовної роботи системи та математичне очiкування безвiдмовної роботи.
11.22.Система складається з n блокiв. Нехай ti – час безвiдмовної роботи i-го блоку. Випадковi величини t1,. . . , tn – незалежнi i мають показниковий розподiл iз параметром . Система працює до того часу, поки працює принаймнi один блок. Знайти функцiю розподiлу часу безвiдмовної роботи системи та математичне очiкування часу безвiдмовної роботи.
11.23.Система складається з n блокiв. Нехай ti – час безвiдмовної роботи i-го блоку. Випадковi величини t1,. . . , tn – незалежнi i мають показниковий розподiл iз параметром . Система працює до того часу, поки з ладу не вийде k блокiв. Позначимо через x час безвiдмовної роботи системи. Обчислити функцiю розподiлу й щiльнiсть розподiлу випадкової величини x.
11.24.Три особи А, В i С приходять до поштового вiддiлення i застають вiльними два вiкна. Обслуговування А i В розпочинається одразу, а обслуговування С розпочинається тодi, коли закiнчиться обслуговування або А, або В. Тривалiсть обслуговування є незалежними однаково розподiленими величинами з показниковим розподiлом. а) Яка ймовiрнiсть того, що С пiде з поштового вiддiлення не останньою? б) Який розподiл i математичне очiкування часу, проведеного С в поштовому вiддiленнi?
11.25. Функцiя розподiлу випадкової величини F (x) = A + B arctg x (розподiл Кошi). Знайти сталi A та B, щiльнiсть розподiлу та ймовiрнiсть попадання значення випадкової величини на промiжок ( 1; 1).
Вiдповiдь. A = 1 |
; B = 1 |
; f(x) = |
1 |
|
; p = 0; 5. |
2 |
) |
||||
2 |
|
|
(1+x |
|
