
Лабы по механике 1.1-1.14
.pdf
гармонических колебаний.
§ 1.3.2. Механические гармонические колебания
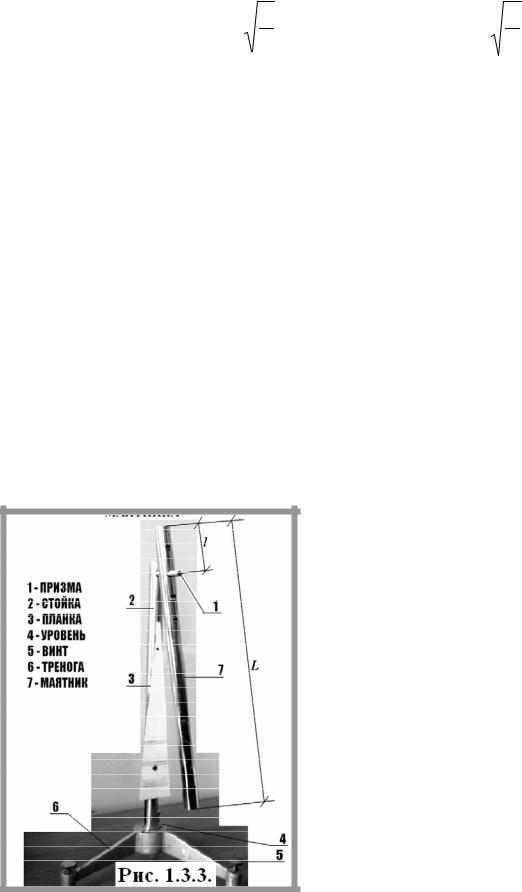
Если материальная точка (МТ) совершает прямолинейные гармонические колебания вдоль декартовой оси координат ОХ около положения
|
|
равновесия, |
принятого за начало |
координат |
|
|
|
(рис.1.3.1), |
то зависимость координаты |
x точки от |
|
|
|
времени t |
имеет вид ( s = x ): |
|
|
|
|
(1.3.5) x = Asin(ωt +α0 ). |
|||
|
|
||||
Проекции скорости υG и ускорения a |
точки на ось ОХ равны соответственно: |
|
|||
(1.3.6) |
|
′ |
|
ax = −a0 sin(ωt +α0 ), |
|
υx =υ0 cos(ωt +α0 ), (1.3.6 ) |
|||||
где υ0 = Aω и a0 = Aω2 = ωυ0 −амплитуды скорости и ускорения соответственно.
Согласно второму закону Ньютона сила, действующая на материальную точку, равна
(1.3.7) |
G |
′ |
) |
Fx = −mω |
2 |
x, |
F = ma, |
(1.3.7 |
|
||||
где m −масса материальной точки. |
|
|
|
|
|
|
Следовательно, в общем случае сила F пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону:
(1.3.8) F = −mω2 xi ,
где i −единичный орт оси ОХ.
§ 1.3.3. Момент инерции твердого тела
Момент инерции тела при вращательном движении аналогичен по смыслу массе при поступательном движении, являясь мерой инертности тела при изменении им угловой скорости под действием вращающего момента.
Моментом инерции тела массой m относительно неподвижной оси OO′ называется физическая величина JOO′ , равная сумме произведений всех бесконечно малых элементов массы dm рассматриваемого тела на квадраты их расстояний r до оси вращения:
(1.3.9) JOO′ = ∫r2dm .
(m)
Момент инерции данного тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси, то есть от распределения массы относительно оси вращения. Согласно теореме Штейнера (теореме о переносе осей инерции) момент инерции тела J относительно произвольной неподвижной оси равен сумме момента инерции этого тела JC относительно оси, проходящей через центр инерции тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d
21

между осями:
(1.3.10) J = JC + md 2 .
Моменты инерции однородных тел простейшей формы относительно осей, проходящих через их центры масс, приведены в таблице № 1.3.1:
|
|
|
Таблица № 1.3.1. |
|||
|
|
|
||||
Наименование тела |
Момент инерции |
|||||
|
|
|
|
|
|
|
полый тонкостенный цилиндр радиуса R, массы m |
|
mR |
2 |
|
||
|
|
|
|
|||
|
|
|
|
|
|
|
сплошной цилиндр (диск) радиуса R, массы m |
1 |
2 |
mR2 |
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
сплошной шар радиуса R, массы m |
2 |
5 |
mR2 |
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
тонкостенная сфера радиуса R, массы m |
2 |
|
3 |
mR2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямой тонкий стержень длины L, массы m |
|
|
|
|
2 |
|
|
112 mL |
|
||||
тонкая квадратная пластина со стороной L, массы m |
1 |
6 |
mL2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
куб со стороной L, массы m |
1 |
|
4 |
mL2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 1.3.4. Гармонические колебания физического маятника
Физический маятник – твердое тело произвольной формы, имеющее возможность качаться под действием его силы тяжести mg ( m −масса маятника, g −ускорение свободного падения)
вокруг неподвижной горизонтальной оси OZ (рис. 1.3.2.), не проходящей через центр тяжести тела. Эта ось перпендикулярна плоскости рисунка («смотрит на нас») и
называется осью качания маятника. Точка O пересечения оси качания маятника с вертикальной плоскостью (плоскостью рисунка), проходящей через центр тяжести маятника (центр инерции), называется
точкой подвеса маятника.
В отсутствие сил трения в
22

подвесе движение физического маятника описывается основным уравнением динамики вращательного движения:
|
(1.3.11) |
JεG = M, |
где J −момент инерции маятника относительно оси ОZ, |
||
G |
d2ϕG |
|
ε = |
dt2 −угловое ускорение, t −время, |
|
dϕ −элементарный вектор поворота, |
ϕ −угол поворота вокруг оси качания, |
|
G |
отсчитываемый от положения равновесия, |
|
M −момент силы mgG, |
|
|
M= −mgd sinϕ − проекция момента силы тяжести на ось ОZ2
Впроекциях на ось ОZ уравнение (9) имеет вид:
(1.3.12) J d2ϕ2 = −mgd sinϕ, dt
где d = OC −расстояние от центра инерции до оси качания. При малых колебаниях sinϕ ≈ϕ , и уравнение движения маятника удовлетворяет дифференциальному уравнению гармонических колебаний (1.3.2):
(1.3.13) d2ϕ |
+ mgd |
ϕ = 0. |
dt2 |
J |
|
Таким образом, в отсутствие трения малые колебания физического маятника являются гармоническими, и угол ϕ изменяется по закону косинуса:
(1.3.14) ϕ =ϕ0 cos(ωt +α0 ),
где ϕ0 −амплитуда колебаний угла ϕ , а циклическая частота ω и период малых колебаний T
равны соответственно:
(1.3.15) ω = |
mgd |
и (1.3.16) |
T = 2π |
J . |
|
J |
|
|
mgd |
§ 1.3.5. Гармонические колебания математического маятника
Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести. Математический маятник представляет собой предельный случай физического маятника, вся масса
2 Знак «–» показывает, что проекция векторов M и dϕ на ось OZ всегда имеют противоположные знаки (за положительное направление угла ϕ принято движение
вправо от положения равновесия).
23
которого сосредоточена в его центре инерции, так что d = l −длина математического маятника.
Момент инерции такого маятника относительно оси качания равен, очевидно, J = ml 2 . Тогда его циклическая частота ωм и период малых колебаний Tм равны соответственно:
(1.3.17) ω |
м |
= g |
и (1.3.18) |
T |
= 2π l . |
|
l |
|
м |
g |
|
|
|
|
|
Заметим, что малые колебания физического и математического маятников являются примером изохронных колебаний, то есть колебаний, частоты и периоды которых не зависят от их амплитуд.
Приведенной длиной физического маятника lпр называется длина математического
маятника, имеющего такой же период колебаний:
(1.3.19) lпр = |
J |
= md 2 + JC = d + |
JC |
> d , |
|
md |
md |
||||
|
md |
|
где JC −момент инерции физического маятника относительно оси, проходящей через центр инерции С маятника и параллельной его оси качания. Точка О1, лежащая на прямой ОС на расстоянии lпр от точки подвеса маятника О (см. рис. 1.3.2), называется центром качания
физического маятника. Центр качания О1 и точка подвеса О обладают свойством взаимности: если физический маятник подвесить так, чтобы его ось качаний проходила через точку О1, то точка О будет совпадать с его новым положением центра качания маятника, то есть приведенная длина и период колебаний маятника останутся прежними.
ОПИСАНИЕ УСТАНОВКИ
Телом, момент инерции которого измеряется в лабораторной работе, служит однородный металлический стержень длиной L (рис. 1.3.3) с четырьмя высверленными отверстиями, расположенными выше его центра тяжести. С помощью отверстий стержень подвешивается на призму 1, и при выведении его из положения равновесия он совершает колебания как физический маятник.
Призма 1 закреплена с помощью штифта на вертикальной стойке 2. Стойка установлена на треноге 6, две ножки которой снабжены винтами 5. Винты позволяют установить прибор по
имеющемуся уровню 4 так, чтобы опорное ребро призмы приняло строго горизонтальное положение.
24
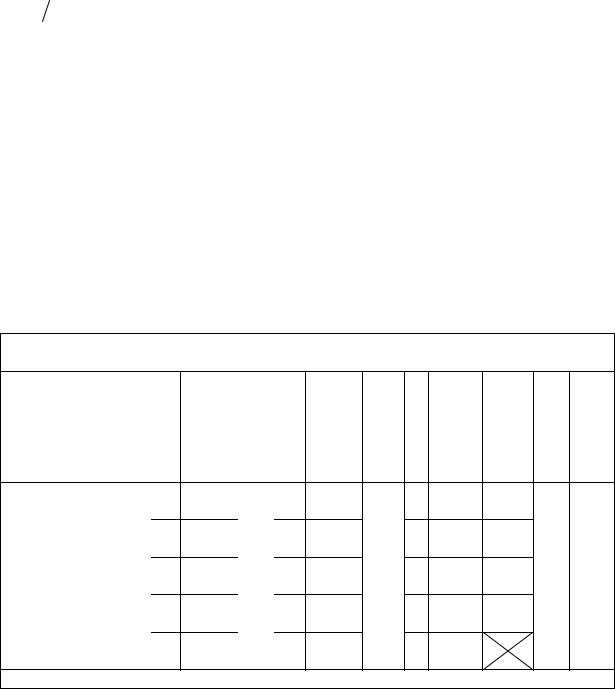
К стойке прикреплена планка 3 клиновидной формы с углом при вершине ±4°. Она является визиром, позволяющим следить за тем, чтобы размах колебаний измеряемого тела не превосходил
± (6...7)D, то есть чтобы колебания можно было считать гармоническими.
На рисунке показаны также общая длина стержня L и расстояние l от верхнего края стержня до его рабочего отверстия. Важно отметить, что нумерация отверстий (осей) идет снизу вверх!
Момент инерции стержня J относительно различных положений оси качания маятника определяют, пользуясь формулой (16) «Теоретических основ работы». Откуда получаем рабочую
формулу для J : |
|
(1.3.20) J = Pt2 (L − 2l) |
, |
8π 2 N 2 |
|
где t − время N полных колебаний стержня весом P = mg , |
|
L 2 − l =d −расстояние от центра инерции до оси качания. |
|
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ, РАСЧЕТЫ
1.Ознакомившись с методическими указаниями к лабораторной работе, получите у обслуживающего персонала задание и распечатку таблицы для занесения экспериментальных данных во время выполнения лабораторной работы.
Примерное задание: |
|
|
|
|
|
Рассчитать момент |
инерции |
стержня относительно осей, проходящих через |
четыре |
||
его отверстия, произведя серию из |
пяти |
измерений 40 полных |
колебаний для каждого |
||
положения оси вращения. |
|
|
|
|
|
Построить график |
зависимости |
момента инерции стержня |
J от положения |
оси |
|
a , отсчитываемого относительно центра масс стержня.
Соответствующий заданию вид распечатки:
Таблица 1.3.2. Журнал экспериментальных измерений
Лабораторная работа № 1.3.
"Определение момента инерции тел методом физического маятника"
N
40
№изм |
t(1),s |
N |
№изм |
|
|
||
1 |
|
|
1 |
|
|
|
2 |
2 |
|
|
|
|
|
40 |
3 |
3 |
|
||
|
|
|
4 |
4 |
|
|
|
|
|
|
5 |
5 |
|
|
|
|
|
|
|
Задание выдано:
t(2),s |
N |
№изм |
|
||
|
|
1 |
|
|
2 |
|
40 |
3 |
|
|
4 |
|
|
5 |
|
|
|
Группа:
t(3),s N
40
ТМС-11,
№изм
1
2
3
4
5
l, P, L,
t(4),s mm H mm
Фамилия: Иванов
25

2.Ознакомьтесь с внешним видом установки, получите у обслуживающего лабораторную работу персонала секундомер и рулетку.
3.Определить общую длину стержня L и расстояние l от верхнего конца стержня до соответствующих отверстий (до их верхних краев). Результаты измерений занесите в таблицу 1.3.2. Внимание! Отверстию с №1 в таблице (первая строка) соответствует ближайшее к центру масс стержня отверстие; далее номера отверстий последовательно растут снизу вверх.
4.Занесите в таблицу 1.3.2 значение веса металлического стержня (см. значение указанной физической величины на лабораторном столе).
5.Приведите стержень в колебательное движение относительно оси, проходящей через первое
(нижнее) отверстие. Размах колебаний не должен превышать ±(6...7)D . Измерьте секундомером время N полных колебаний (см. задание). Результат 1-го измерения 1-ой серии колебаний стержня занесите в таблицу 1.3.2. Выполните еще четыре измерения (для примерного задания) времени N полных колебаний в этой серии (для этого же положения оси вращения). Результаты снова занесите в таблицу 1.3.2.
6.Повторите опыт для колебательного процесса стержня относительно второй, третьей и четвертой осей, проведя соответственно измерения времени N полных его колебаний по пять раз (2-ую, 3-ью и 4ую серии измерений для примерного задания). Всякий раз результаты заносите в таблицу 1.3.2.
Внимание! Верхнее отверстие отвечает 4-ой серии измерений (в таблице 1.3.2 – столбец время t(4)).
7.Изучите исходные данные таблицы 1.3.3 основного лабораторного окна программы обработки экспериментальных данных (для примерного задания).
Таблица 1.3.3. Основное лабораторное окно
ИСХОДНЫЕ ДАННЫЕ ПРОГРАММЫ (желтый фон столбцов)
N |
─ количество |
полных |
колебаний стержня |
|
относительно 1-ой…4-ой осей качания; |
||
t(1)...t(4), |
─ времена, |
отвечающие N |
полным колебаниям |
|
стержня относительно 1-ой…4-ой осей качания; |
||
26
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Sокр(N ) |
|
─ |
среднеквадратичная |
погрешность |
|
округления |
|||
|
|
количества полных колебаний |
N ; |
|
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
Sсуб(t) |
|
─ среднеквадратичная |
субъективная |
погрешность |
|||||
|
|
при измерении времени секундомером; |
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|||
l , |
|
─ расстояние от |
верхнего |
конца |
стержня |
до верхнего края |
|||
mm |
|
|
соответствующего отверстия в нем (до точки подвеса); |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
pi |
|
─ число π , |
количество знаков после запятой в |
||||||
|
|
|
котором определяет экспериментатор; |
|
|||||
Smax (pi) |
|
─ максимальная |
среднеквадратичная |
погрешность |
|||||
|
|
числа π ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
g , |
m/s2 |
─ |
константа, |
нормальное |
ускорение |
свободного |
|||
|
|
|
падения, количество знаков после запятой в |
||||||
|
|
|
которой определяет экспериментатор; |
|
|||||
Smax (g), |
|
─ максимальная |
среднеквадратичная |
погрешность |
|||||
|
|
константы |
g ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m/s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Sпрок(t), |
|
─ среднеквадратичная |
систематическая (приборная + |
||||||
|
|
погрешность |
|
округления) |
|
|
погрешность |
||
|
|
|
|
|
|
||||
s |
|
|
секундомера; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Sприб(L, l), |
─ среднеквадратичная |
приборная погрешность при |
|||||||
|
|
|
измерении величин L, l ; |
|
|
|
|||
mm |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Sсуб(l), |
|
─ среднеквадратичная |
субъективная погрешность при |
||||||
|
измерении величины l ; |
|
|
|
|
||||
|
|
|
|
|
|
||||
mm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Sокр(L, l), |
─ среднеквадратичная |
погрешность |
округления при |
||||||
измерении величин L, l ; |
|
|
|
||||||
|
|
|
|
|
|||||
mm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P , |
|
─ вес стержня; |
|
|
|
|
|
||
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Smax (P), |
|
─ максимальная |
среднеквадратичная |
погрешность |
|||||
|
|
константы |
P ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L, |
|
─ длина стержня. |
|
|
|
|
|
||
mm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27

|
|
|
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ТАБЛИЦЫ 1.3.3, |
|
|
|||||||||||
|
ВЫЧИСЛЯЕМЫЕ ПРОГРАММОЙ (серый фон столбцов) |
|
|
|||||||||||||
< t(1)> ... < t(4)>, |
s |
|
─ средние |
|
арифметические |
времена, |
||||||||||
|
|
|
|
|
|
отвечающие N полным колебаниям стержня |
||||||||||
|
|
|
|
|
|
относительно 1-ой…4-ой осей вращения; |
||||||||||
S(t(1))...S(t(4)), |
|
s |
|
─ среднеквадратичные |
|
случайные |
погрешности |
|||||||||
|
|
|
|
|
|
величин времени |
t(1)...t(4) |
|
|
колебаний |
стержня |
|||||
|
|
|
|
|
|
относительно 1-ой…4-ой осей вращения; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
J0 , |
|
кг*m |
2 |
|
|
─ момент инерции |
стержня |
|
относительно |
центра |
||||||
|
|
|
|
масс (вычисленный); |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a = L 2 − l , |
mm |
|
|
─ расстояние |
от |
центра |
масс |
стержня |
до 1- |
|||||||
|
|
|
|
|
|
ой…4-ой осей качания; |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
J , |
|
кг*m2 |
|
─ момент |
инерции |
стержня |
относительно 1- |
|||||||||
|
|
|
|
|
|
ой…4-ой осей качания; |
|
|
|
|
|
|||||
S(J ), |
кг*m2 |
|
─ суммарная |
|
|
|
|
|
среднеквадратичная |
|||||||
|
|
|
|
|
|
погрешность |
момента инерции |
J относительно 1- |
||||||||
|
|
|
|
|
|
ой…4-ой осей качания. |
|
|
|
|
|
|||||
|
|
|
|
|
||||||||||||
|
Вычисление |
искомой величины |
J программа производит |
согласно |
||||||||||||
|
формуле (1.3.20) «Теоретических основ работы», в которой все величины |
|||||||||||||||
|
берутся в системе СИ: |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
J = |
P(L − 2l)< t >2 |
|
. |
|
|
|
||||
.1ПРИМЕЧАНИЕ |
|
|
|
|
|
|
8π 2 N 2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При |
оценке |
|
систематических |
среднеквадратичных погрешностей |
||||||||||||
|
|
|||||||||||||||
|
Sприб(L,l), Sокр(L,l), Sпрок(t), Sокр(N ), Smax (g) и Smax (P) |
|||||||||||||||
|
величин |
L, l, t, |
N и констант |
g |
и |
P |
воспользуйтесь |
указаниями |
||||||||
|
«Краткой теории погрешностей» (§П.2.3). |
|
|
|
|
|
|
|
||||||||
|
Внимание. В данной работе следует принять |
|
следующие значения |
|||||||||||||
|
среднеквадратичных погрешностей: |
Sсуб(t)= 0,3 c и Sсуб(l)= 0,5 мм. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.2 ПРИМЕЧАНИЕ
Программа обработки данных, производя вычисление всех
среднеквадратичных |
погрешностей, |
строит |
график |
зависимости |
|||
S(J )1 = |
f (S′(J )1 ) |
суммарной |
среднеквадратичной погрешности, где 1 − |
||||
номер |
1-го отверстия, |
от |
вклада |
других погрешностей |
по методике, |
||
которая подробно рассмотрена и применена в работах №№ 1.1 и 1.2 настоящего практикума.
Вывод на печать графика функции S(J )1 = f (S′(J )1 ) производится по нажатию кнопки G1 (см. таблицу 1.3.2).
28
.3 ПРИМЕЧАНИЕ
Процедура вычисления |
среднеарифметического |
значения |
< t(i) > и |
||||
среднеквадратичной случайной погрешностей |
S(t(i)) величины |
t(i), где |
|||||
i − номер |
отверстия, |
а |
также доверительного |
интервала |
искомой |
||
физической |
величины |
J , |
кроме того, |
оформление |
результатов |
||
лабораторной работы (запись окончательного результата, построение графиков) программа выполняет следуя указаниям «Краткой теории погрешностей» (см. §§ П.2.3, 5, 6).
Единицы длины, времени и единица измерения ускорения в таблице №1.3.2 обозначены латинскими буквами (mm, s и m/s2 соответственно) в силу особенностей воспроизведения строковых констант программой обработки данных.
.4 ПРИМЕЧАНИЕ
Среднеквадратичную суммарную погрешность S(J ) искомой величины J
программа вычисляет согласно «Основным правилам обработки результатов косвенных измерений» (см. § П.2.4 «Краткой теории погрешностей»). Например,
для среднеквадратичной суммарной погрешности S(J )1 момента инерции J1
относительно первой оси:
S(J ) |
= |
|
|
(L |
− 2l)< t |
1 |
>2 |
|
2 |
(P)+ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
8π |
N |
2 |
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
P |
< t |
|
> |
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
+ |
8π |
2 |
N |
|
|
|
|
{Sприб |
(L)+ Sокр(L)}+ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
P < t |
|
> |
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+ |
4π |
2 |
N |
2 |
|
|
|
|
{Sприб |
(l)+ Sокр(l)+ Sсуб(l)}+ |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
P(L − 2l)< t > |
2 |
{S2 (t |
|
)+ S2 |
|
|
(t)+ S2 |
|
|
(t)}+ |
|
|
|
|
|||||||||||||||||||||
+ |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
4π 2 N 2 |
|
|
|
|
|
|
|
|
1 |
прок |
|
|
|
суб |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
P(L − 2l)< t >2 |
2 |
|
|
(pi)+ |
|
P(L − 2l)< t >2 |
|
2 |
(N ) . |
||||||||||||||||||||||||||
+ |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
S2 |
||||||
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||
|
|
|
4π |
N |
|
|
|
|
|
max |
|
|
|
|
|
|
4π |
N |
3 |
|
|
окр |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
29
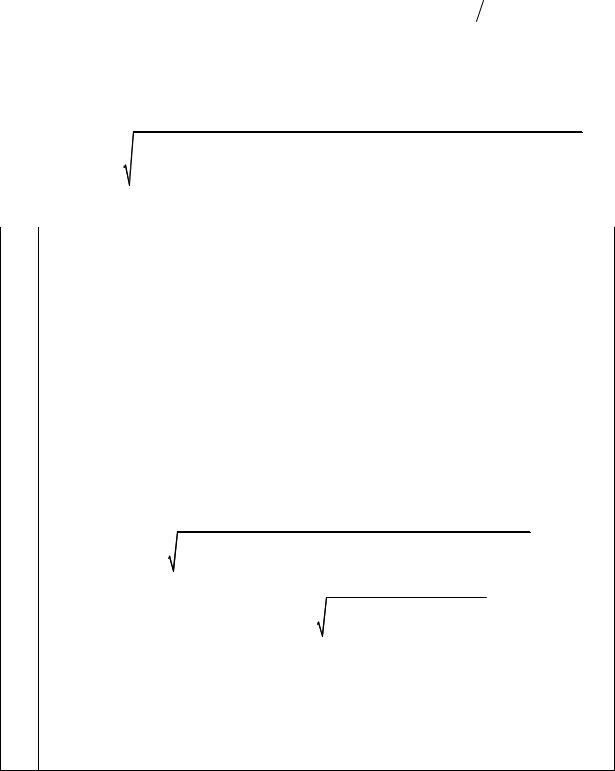
|
Вычисление величины J0 программа производит согласно |
|||||||||||||||||
|
формуле из таблицы №1.3.1 «Теоретических основ работы», в |
|||||||||||||||||
ПРИМЕЧАНИЕ |
которой все величины берутся в системе СИ: |
J0 = PL2 (12g). |
||||||||||||||||
Среднеквадратичную |
суммарную |
погрешность S |
(J0 ) |
величины J0 , |
||||||||||||||
|
||||||||||||||||||
|
которая используется при построении графика функции |
J = f (a), программа |
||||||||||||||||
|
вычисляет согласно «Основным правилам обработки результатов косвенных |
|||||||||||||||||
.5 |
измерений» (см. § 2.4 «Краткой теории погрешностей»): |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
2 |
|||
|
S(J0 )= |
L |
|
Smax2 (P )+ PL |
|
|
{Sприб2 |
(L)+Sокр2 |
(L)}+ |
PL |
|
Smax2 (g) . |
||||||
|
|
|
2 |
|||||||||||||||
|
12g |
|
6g |
|
|
|
|
|
|
|
|
12g |
|
|
||||
|
|
|
||||||||||||||||
|
График зависимости J = f (a) |
момента инерции стержня от расстояния, |
||||||||||||||||
|
отсчитываемого от его центра масс, |
программа строит поточечно, используя в |
||||||||||||||||
|
качестве аргумента рассчитанные расстояния a |
от центра масс |
стержня до 1- |
|||||||||||||||
|
ой…4-ой осей вращения, а качестве функции – соответствующие |
|||||||||||||||||
|
рассчитанные значения момента инерции J . Для построения первой |
|||||||||||||||||
|
точки используется координата (a = 0; |
J0 ). |
|
|
|
|
|
|
||||||||||
|
Среднеквадратичная суммарная погрешность S(a) |
|
любого аргумента a , |
|||||||||||||||
.6ПРИМЕЧАНИЕ |
кроме a = 0 , вычисляется программой согласно «Основным правилам обработки |
|||||||||||||||||
S(a)= |
1 {Sприб2 |
(L)+Sокр2 |
(L)}+Sприб2 |
(l )+Sокр2 |
(l )+Sсуб2 |
(l ) . |
||||||||||||
|
результатов косвенных измерений» (см. § П.2.4 «Краткой теории |
|||||||||||||||||
|
погрешностей»): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для аргумента a = 0 имеем: S(a = 0)= |
14 {Sприб2 |
(L)+Sокр2 |
(L)} . |
|
|
||||||||||||
Для каждой ординаты и абсциссы программа фиксирует погрешность, откладывая вверх и вниз, влево и вправо величину доверительного интервала. На графике получается прямоугольник погрешности для каждого экспериментального значения.
8. Переходите к автоматизированной системе на свободный компьютер, предварительно ознакомившись с инструкцией по использованию программы обработки экспериментальных данных (см. П.1).
9. Произведите вычисление результата, расчет погрешностей и построение графика функции
J = f (a) с помощью программы обработки экспериментальных данных. Подготовьте
результаты к печати.
10. Распечатайте отчет: числовой результат в системе СИ вместе с погрешностями (абсолютной и относительной) с учетом коэффициента доверия, а также графический результат (на обороте
30
