Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет международных отношений МИД России (МГИМО)

Предмет:

Линейная алгебра

Файл:

ЛинАл Задачник - Малугин.pdf

Скачиваний:

164

Добавлен:

08.03.2016

Размер:

6.79 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1816 17 18 > Следующая >>>

Глава 7

Классические методы оптимизации

112

Глава 7. Классические методы оптимизации

1 . Л о к а л ь н ы й

э к с т р е м у м

ф у н к ц и и

z f x,

y .

Точка M0 x0, y0 называется

точкой

локального экстремума функции z f x,

y ,

если существует окрестность точки M

0 , такая, что для всех

точек M x, y из этой

окрестности выполнено

неравенство

f x0 , y0 f x, y

(строгий локальный

максимум) или неравенство f x0 , y0 f x, y

(строгий локальный минимум).

Теорема 1. (Необходимые условия экстремума). Если точка M 0 x0 ,

y0 есть точка локального

экстремума, то

x0 , y0

0 , zy

x0 , y0

0 .

Теорема 2. (Достаточные условия экстремума). Если в точке M 0 x0 ,

y0 выполнены необходимые

условия экстремума и все частные производные 2-го порядка непрерывны, то существование экстремума в
точке M 0 x0 ,	y0	определяется значениями угловых миноров матрицы вторых производных (гессиана)
			z	z	,
			xx	xy	,
		z yx		z yy

а именно:

1)M1 0, M 2 0 - локальный минимум;

2)M1 0, M 2 0 - локальный максимум;

3)M 2 0 - экстремума нет.

Для исследования на локальный экстремум функции трех переменных рассматривается матрица


	uxx		uxy		uxz


	u yx		u yy		u yz
u			u		u
		zx		zy		zz

и изучаются ее угловые миноры.

2 . У с л о в н ы й э к с т р е м у м . Экстремум функции z f x, y достигнут при условии, что аргументы функции связаны уравнением g x,

связи. Для нахождения условного экстремума составляется функция Лагранжа

L x,	y f x,	y g x,	y c ,
которая исследуется на экстремум при
дополнительном условии g x dx g y dy 0 .
3 . Г л о б а л ь н ы й		э к с т р е м у м .

Глобальные максимум и минимум определяются как наибольшее и наименьшее значения функции в области определения, состоящей из внутренних точек области и множества точек границы области.

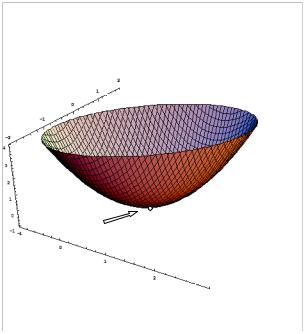
ПРИМЕР 1. Исследовать на экстремум функцию u 2x2 2 y 2 2xy 4x 2 y 1 .

Решение. Найдем частные производные 1- го порядка, приравняем их нулю и запишем получившиеся уравнения в виде системы

4x 2 y 4 0 .4 y 2x 2 0

Решая систему уравнений, получим единственную стационарную точку x 1, y 0 .

Найдем частные производные 2-го порядка

называется условным, если он y c , называемом уравнением

Рис. 7.1

Глава 7

Классические методы оптимизации

113

2 .

y 2

x y

Составим гессиан из вторых производных

x 2

x y

1, 0

Угловые миноры матрицы( M1 4, M2

12 )

положительны. Следовательно,

в стационарной точке

достигается минимум:

umin 1, 0 1 . График функции в трехмерной системе координат представлен на

рис. 7.1. Минимум функции указан стрелкой. Заметен характерный для функции желоб вдоль прямой y x ,

образуемой

группой

слагаемых

x2 2xy y 2 . Верхняя часть графика

срезана для наглядности плоскостью

u 5 .

-1

ПРИМЕР 2. Исследовать на

N 2

экстремум функцию

u y 6 x4 y 4 2x2 3 .

Решение. Делаем преобразова-

ния аналогично предыдущему при-

N 4

меру: находим производные, прирав-

ниваем их нулю, находим стационар-

ные точки, решая систему уравне-

ний:

					u			4x 4x				3	0,							-1
						x		4x 4x					0,
						u									.								0
						y		4 y3 6 y5 0
						y																							1		x
																															x
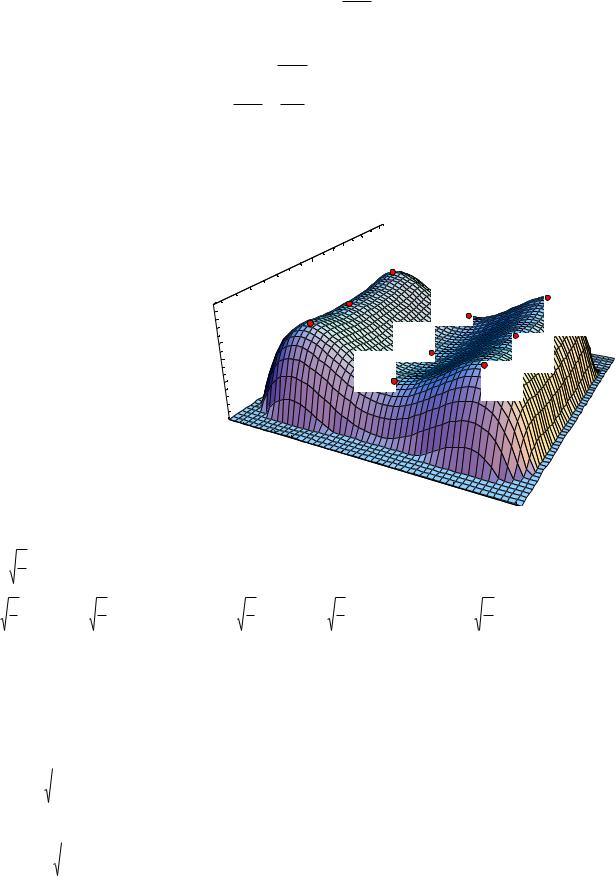
Получим девять стационарных																								Рис.7.2.
точек:																								Рис.7.2.
точек:
										1, 0 ,
N	1	1,		2 , N				2		1, 0 ,
	1			3				2
				3

			2								2				0, 0 ,				2			2				1, 0					2
N	3	1,	2		,	N	4		0,		2	,	N	5	0, 0 ,	N	6	0,	2	, N	1,	2	,	N	8	1, 0	,	N	9	1,	2	.
	3		3				4				3			5			6		3		7	3			8				9		3
			3								3								3			3									3

Найдем вторые частные производные и составим из них гессиан

2u	2u


x 2	x y		4 12x 2
2u	2u		0
2u	2u		0
		2

x y	y
x y	y

		0
12 y	2	30 y	4	.
12 y		30 y

Рассмотрим поведение гессиана во всех стационарных точках.

								4 12x2							4	0
		2						4 12x2					0		4	0
1) Точки	0,				. Гессиан											16	.
1) Точки	0,				. Гессиан											16	.
		3						0		12y		2	30y	4	0
												2		4	0	3
																3
Угловые миноры M1 0, M 2							0 . Экстремума нет.
								8	0
			2					8	0
2) Точки	1,					. Гессиан			16		. Угловые миноры M								0, M		0 . Следовательно, функция имеет
2) Точки	1,					. Гессиан			16		. Угловые миноры M								0, M		0 . Следовательно, функция имеет
								0										1		2
				3					3

в этих точках максимум:

Глава 7			Классические методы оптимизации				114


u		1,	2		112	.
u		1,				.
	m ax		3	27
			3	27

3)	Точка 0,	4	0	минор M 2 0 . Критерий Сильвестра				не	работает. Для
		0 . Гессиан	. Угловой
		0	0
исследования поведения функции в точке 0,				0 рассмотрим приращение функции в этой точке
		u u x, y u 0, 0 y6 x4 y4 2x2 x2 2 x2 y4 1 y2 .
	При любых малых отклонениях точки x,				y от точки 0,	0 величины	2 x2	и	1 y 2 положи-
тельны. Поэтому приращение u 0 . В точке 0,					0 достигается минимум: umin 0,		0 3 .
4)	Точки 1,	0 . Угловой минор M 2 0 . Рассуждая способом, аналогичным пункту 3, найдем, что в этих

точках экстремума нет. График функции представлен на рис. 7.2.

ПРИМЕР 3. Исследовать на условный экстремум функцию u 2x 2y 4 при условии

2x 2 y 2 6 .

Решение. Первый способ решения задачи на условный экстремум, а именно, выражение одной переменной через другую в уравнении связи и подстановка в исследуемую функцию приводит к необходимости рассматривать два случая. Оба случая содержат радикалы, в результате чего исследование

становится		достаточно громоздким.																Использование функции Лагранжа позволяет избежать громоздких
преобразований. Составим функцию Лагранжа
																	L x,				y 2x 2 y 4 2x2 y 2 6 .
Найдем частные производные 1-го порядка функции Лагранжа
																					L	2 4 x, L 2 2 y .
																					x	y
Для нахождения стационарных точек составим систему из трех уравнений, приравняв нулю первые
производные и взяв уравнение условия.
								2 x 0,
					1			2 x 0,
					1			y			0, .
					2x2					y2				6											-2
																									-2
Решая систему, выразим х из первого уравнения, у																										0
Решая систему, выразим х из первого уравнения, у																											2
из второго и подставим в третье. Получим две																											2	y 4
из второго и подставим в третье. Получим две																												y 4
стационарные точки. Для													1			имеем
												1			2
															2
x 1,		2 . Для								1 имеем x									1,			2 .						10
x 1,	y	2 . Для							2	1 имеем x									1,		y	2 .
1	1								2			2					1				1
												2
Найдем все вторые частные производные																												0
																												0
функции Лагранжа.
			2 L	4 ,						2 L				2 ,			2 F				0 .							x
		x2		4 ,						y 2				2 ,			x y				0 .
		x2								y 2							x y											2
																												2
Составим гессиан из вторых производных																											1
					2 L					2 L															0
																4 0							-1
				x2						x y													-1
				x2						x y
							2				2							.				-2
							2	L			2	L					2					-2
								L				L				0	2
					x y					y		2											Рис. 7.3.
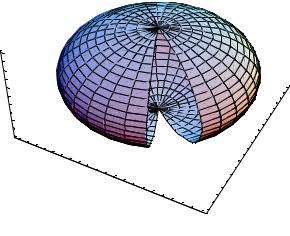
					x y					y													Рис. 7.3.
1) 1 , x				1, y							2 .					Угловые					миноры
	1	2	1							1
		2																			Следовательно, в стационарной точке 1,					2 достигается
матрицы ( M1 2, M2								2 )				положительны.									Следовательно, в стационарной точке 1,					2 достигается
минимум: umin 1,					2 2 .
2)			1 , x			1,				y		2 . Угловые миноры имеют разные знаки, причем M												1	2, M	2	2 .
	1		2	1						1														1		2
			2																	2 достигается максимум: umax 1,			2 10 .
Следовательно, в стационарной точке 1,																				2 достигается максимум: umax 1,			2 10 .

Глава 7								Классические методы оптимизации			115
О наличии экстремум можно судить по виду 2-го дифференциала функции Лагранжа
d 2 L	2 L dx 2 2		2 L	dxdy	2 L dy 2			4 dx 2 2 dy 2 2 2dx 2 dy 2 .

	x2		x y		y 2
При 0 получим	d 2 L 0 ,	что соответствует						минимуму функции	Лагранжа, а, следовательно,
условному минимуму исследуемой функции: u					min	1,		2 2 . При 0	получим d 2 L 0 - максимум
									u : umax 1,	2 10 .
функции Лагранжа, соответственно – условный							максимум функции				Графики

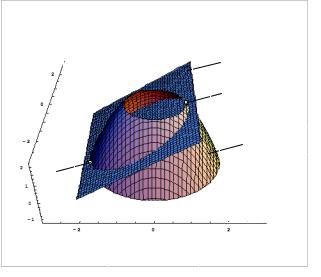
исследуемой функции и неявной функции, задающей условие, приведены на рис. 7.3. На графике указано положение максимума. Минимум скрыт за поверхностью цилиндра. Для лучшего обзора пересечений поверхностей из цилиндра вырезан сегмент.

1 1

ПРИМЕР 4. Исследовать на условный экстремум функцию u 5x14 x22 при условии 13x1 10x2 12 . Решение. Воспользуемся функцией Лагранжа:

1 1

L 5x14 x22 13x1 10x2 12 .

Найдя частные производные, приравняем их нулю

				1
				1
	L	5x22				13 0,
	L					13 0,
	x1	3

		4x 4
		1
					1
					1
			5x 4
L			1				10 0,
L							10 0,
	x21	1
	x21	1

			2x22

Перенесем вторые слагаемые вправо и разделим одно уравнение на другое. Тогда

Подставим это соотношение в уравнение связи. Получим

координаты	критической					точки						x			4					, x	2		4 .		Вторые
													1				13				2		5
																	13						5
частные производные равны:
			1								1
L		15x 2		, L					5x		4	,		L								5		.
L			2	, L						1		,		L								3 1		.
x1x1			7		x2x2						3					x1x2						3 1
		16x14							4x22											8x		4 x 2
																					1		2
Составленный из них гессиан
												1
												1
										15x2							5
												2
												7					3		1
										16x		4		8x			4	x	2
		Lx1x1		Lx1x2						16x				8x				x	12
			L	L							1					1			12
			L	L
			x1x2	x2 x2						5						5x			4
																		1
										3		1							3
								8x14 x22								4x22
имеет угловые миноры разного знака, причем																													0
имеет угловые миноры разного знака, причем
										1
				M			15x 2				0			,
				M	1					2	0			,
					1					7
							16x 4
										1
																		1					1				2
															15x 2								5x 4			5		25
								M 2										27					13			3 1		3	0 .
																		4					2			4 2		2	x2
															16x1								4x2			8x1 x2		32x1	x2

x2	13 или x		2		13 x .
2x1	10		2			5	1
2x1	10					5
0
	0.25
		0.5
		0.75 x2
						1
							5
							4
							3
							2
							1
				x1			0
							0
						1
		0.75
		0.5
0.25

Рис.7.4.

Следовательно, в точке с координатами x1 134 , x2 54 достигается максимум

4			4	2		10	3,331.
zmax		,
	13		5	4
					13

Геометрическая иллюстрация приведена на рис. 7.4, где стрелкой указан максимум функции.

Глава 7

Классические методы оптимизации

116

ПРИМЕР 5. Исследовать на условный экстремум функцию при условии .

Решение. Функция Лагранжа для нашей задачи имеет вид

(

)

(

)

Необходимые условия позволяют найти стационарные точки

	{
Выразим из первых трех уравнений	через λ

и подставим в последнее уравнение. Получим

Его решение

дает две стационарные точки. При

имеем

(точка

), при

имеем

(точка

Достаточные условия требуют знания вторых производных

Воспользуемся окаймленным гессианом 4-го порядка

\|	\|	\|	\|	\|	\|.
		\|	\|

1)	(		) В этой точке \| \|\|	\|	\|	.
Поскольку \|		\|	экстремума нет.
2)	(	)	Можно увидеть, что окаймленный			гессиан \| \|\|	(	)	\|	\|\|	и,
следовательно, имеет тот же знак. Экстремума также нет.
Замечание. В предыдущей задаче окаймленный гессиан \|						\| не был использован. Это связано с тем,
знак \|	\| указывает на минимум или максимум при условии,				что отрицательный знак			\|	\|	определяет

наличие экстремума. В нашей задаче определитель \|			\| оказался больше нуля.
ПРИМЕР 6. Исследовать на условный экстремум функцию
	{		(	)
Решение. Составим функцию Лагранжа
(	)		(	)	(	).
Найдем частные производные		. Равенство нулю частных производных вместе с уравнениями
связи приведет к системе из 5-ти уравнений

{

Глава 7 Классические методы оптимизации 117

Поскольку система уравнений является линейной, построим расширенную матрицу и воспользуемся методом Гаусса-Жордана

\|		\|	.
\|		\|
(	) (		)
Следовательно,	Вторые производные функции Лагранжа

Составленный из них окаймленный гессиан 5-го порядка имеет вид

Расчет дает число |

. Отрицательный знак окаймленного гессиана 5-го порядка указывает

на условный максимум функции 3-х переменных с 2-мя уравнениями связи.

(

)

ПРИМЕР 7. Исследовать на экстремум неявно заданную функцию u u x, y :

6 12u 4u 2 12x 4x2 2 y y 2 0 .

Решение. Введем обозначение

F x, y,

u 6 12u 4u 2 12x 4x2 2 y y 2 .

Найдем первые частные производные

12 8x,

F 2 2 y, F

12 8u .

Решая систему уравнений

12 8x 0,

2 2 y 0

получим стационарную точку x

, y -1 . Подставим эти значения в исходное уравнение, найдем u :

u1 4, u2 1. Итак, имеем

1, 4

1, 1 .

Найдем вторые частные производные

2 F

8 ,

2 F

2 ,

2 F

0 .

y 2

x y

Составим гессиан из вторых производных для неявно заданной функции

			F
			xx
			Fu
			F
			xy
			Fu
			Fu

	3		1,
1) В точке		,
1) В точке		,
	2

F	8
xy

Fu		0
	8u 12	0
	8u 12
F			2	.
F			2
yy	0


Fu
Fu			8u 12

4 гессиан имеет вид

2.5

0
	0
-2.5
0	-2.5
0
	2.5
	-5

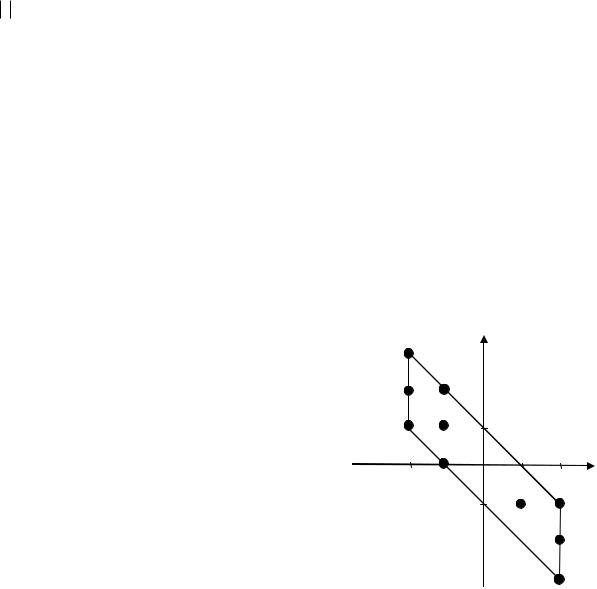
Рис. 7.5. 5 x

				Глава 7			Классические методы оптимизации			118
		2
			0					1
		5	0				причем M1		0 , что соответствует максимуму:
					. Угловые миноры имеют разные знаки,

			1
	0		1					3

			10
			10
		3
umax			, 1			4 .
umax			, 1			4 .
		2

				2
	3					0		3
						0
				гессиан 5
2) Для точки		, 1,	1			1	указывает на существование минимума:	um in	, 1	1 . График
2) Для точки		, 1,	1				указывает на существование минимума:	um in	, 1	1 . График
	2				0			2

						10
						10

неявной функции с вырезанным сектором изображен на рис. 7.5.

ПРИМЕР 8. Определить глобальный экстремум функции

u 3x2 2 y 2 4xy 2x 3

в области x 2, 1 x y 1 x .

Решение. Построим заданную область (рис. 7.6. ). Поскольку дифференцируемая в ограниченной замкнутой области функция достигает глобального максимума или минимума в стационарных точках или на границе области, рассмотрим несколько случаев.

Исследование во внутренних точках области.

1) Найдем стационарные точки. Из решения системы

4 y 2 0,

4 y 4x 0

находим единственную стационарную точку 1,

1 . Она принадлежит рассматриваемой области.

u1 1, 1 2 .

Исследование на границе области.

2) x 2,

. На прямой x 2

функция u имеет вид u 2 y 2 8 y 11 . Критическая точка

1 y

0 . Это точка 2,

2 . Найдем значения функции в точке 2,

2 , а также на

находится из условия u y

концах отрезка в точках

1 и 2,

3 . Они равны u2 2,

2 3 ,

u3 2, 1 5 ,

u4 2,

3 5.

x 2,

. На этой границе функция u

имеет вид

u 2 y 2 8y 19 .

Условие

u y

дает

3 y 1

точку 2,

2 .

Точки концов отрезка:

1 .

Поэтому

2 11 ,

3 13 ,

13 .

y 1 x

y 1 x,

Вид

функции

этой

области:

x 2

u x2 2x 5 .

Критическая

точка

0 .

ней

функция

u8 1,

0 4 .

1 и

2, 3

принимает значение

Точки

-2

-1

уже рассмотрены.

y 1 x,

. Вид функции такой же:

u x2

2x 5 .

y 1 x

2 x

3 ,

2 ,

-1

Соответствующие

точки

также

x 2

рассмотрены.

Выбираем из найденных значений функции наибольшее

и наименьшее:

ugl .min 1,

1 2 ,

ugl .max 2,

3 ugl .max 2,

1 13 .

Рис. 7.6.

ПРИМЕР 9. Найти множество векторов x x1 ,

x2 , минимизирующих функцию

F x ,

22 12x 2x 2

3 x

8x2

и найти минимальное значение функции.

Решение. Найдем стационарные точки функции F x1 ,

x2 .

Глава 7					Классические методы оптимизации						119
		Fx 4 x1 2x2 3 0,						,
			1		2x2 3 0			,
		Fx 8 x1			2x2 3 0
			2
откуда x1 2x2 3 , т.е существует бесконечное множество пар x1 ,								x2 , удовлетворяющих необходимым
условиям экстремума.
Вторые частные производные:	Fx x		4, Fx x		16, Fx x	8 . Легко			проверить,	что критерий
	1	1	2	2	1	2
Сильвестра не работает. Поэтому найдем второй дифференциал:
d 2 F 4dx12 16dx1dx2 16dx22 4 dx1 2dx2 2 0 .
Следовательно, в точках, связанных соотношением					x1 2x2	3 ,	достигается минимум.			Совокупность
векторов, для которых функция F x1 ,	x2	принимает наименьшее значение,							которое оказывается равным

4, имеет вид

x1		2	3
x		c		, где c R .
x2		1	0
ПРИМЕР 10. Найти экстремум в системе функций
	{
Решение. На этой простой задаче, которая может быть решена элементарными методами,
продемонстрируем, как работает метод Лагранжа.
Составим функцию Лагранжа
( )		(		)	(	).

Из условий 1-го порядка найдем критические точки

{

Второе уравнение дает

, т.к.

Из 1-го уравнения найдем

. Решим третье

уравнение, в котором

Его корни

(

Для

)

имеем систему {

Ее решение:

Первая критическая точка

{

Для

имеем систему {

Ее решение:

Вторая

критическая

точка

(

)

{

Найдем вторые частные производные

исоставим

матрицу Гессе (		) (			).
1. В	точке	{		}		матрица Гессе равна	Рис. 7.7
1. В	точке	{		}		матрица Гессе равна

(	)	(	)			). Угловые миноры
		(	)
		(
		(				)
		(				)

Глава 7				Классические методы оптимизации		120
	(		)
2. В точке {		} матрица Гессе равна (		). Угловые миноры	(	)

На рис.7.7 представлено графическое изображение задачи. Верхняя часть параболоида вращения срезана. Замечание. Достаточные условия могут быть реализованы с использованием окаймленного гессиана.

В точке

{

}вычисляем гессиан

, т.е. имеем минимум.

| |

В точке

{

} величина гессиана | | |

| положительна и равна 9. Получаем максимум.

Локальный экстремум

1. Сформулировать определение локального экстремума функции двух переменных

2. Для функции 3-х переменных написать необходимые условия локального экстремума.

3. Что называется критической точкой функции? стационарной точкой?

4. Чему равен 1-й дифференциал функции в стационарной точке?

5. Что можно сказать о существовании локального экстремума в критической точке?

6. Сформулировать достаточные условия локального экстремума, используя угловые миноры.

7.Сформулировать достаточные условия локального экстремума, используя квадратичную форму.

Исследовать функцию на локальный экстремум:

z x2 y 1 2 .

zmin 0,

1 0

z x 2 2 ( y 1)2 3

zmin 2,

1 3

10.

z x2

y 1 2 .

Экстремума нет

11.

z x y 1 2 .

Нестрогий минимум z 0

в точках прямой x y 1 0 .

12.

z x2 xy y2 2x y

zmin (1;0 ) 1

13.

z x2 y 0,5y 2 7 y 12x

zmin 1,

6 30

14.

z 2x3

3x2 3y 2 6xy 36x 18 y 35

zmin 3,

6 100

15.

z 2xy 2 x2 y 4xy 6x 6

Экстремума нет.

16.

z 2x3

6xy 2 3x2 y 78x

zmin 4,

1 208

zmax 4,

1 208

17.

z y3

2 y 2 x y 2x 1

Экстремума нет.

18.

z y3

3x2 y 12x 15 y 10

zmin 1,

2 18 ,

zmax 1,

2 38

19.

z x3

3xy 2 15x 12 y 5

zmin 2,

1 33 ,

	Глава 7		Классические методы оптимизации																						121


					zmax 2,						1 23

20.	z x3 y3 3xy .				zmin 1,		1 1

21.	z x2 xy y 2	2x y .	zmin 1,	0 1

			zmax 2,	3 108 ; нестрогий минимум
22.	z x2 y3 6 x y .		zmin 0,	0 y 6 0 ; нестрогий максимум
				y 0,		0 .
			zmax 0,	y 6		0 .


23.	z x4 y 4 x2	2xy y 2 .					zmin 1,						1 zmin 1,											1 2 .

					zmax 0,			0 0 ;										1									9
24.	z 2x4 y 4 x2 2 y 2 .												zmin						,				1					.
24.	z 2x4 y 4 x2 2 y 2 .												zmin					2	,				1				8	.
																		2									8

25.	z e x2 y 5 2x y .																Экстремума нет.

26.	z x2 xy y 2	4ln x 10 ln y					zmin 1,					2 7 10ln 2 0,0685 .

							1						1							1
					z					,												0,184 ;
					z					,												0,184 ;
						min		2e												2e
27.	z xy ln( x2 y 2 ) .							2e						2e						2e
27.	z xy ln( x2 y 2 ) .														1					1							1
															1					1							1
									z																			.
									z																			.
											max					2e										2e
																2e					2e					2e


			zmax 1,	1 6 ,	zmin x,	y 2 , где х,
28.	z 2	14 2x 2y x2 y2		у	связаны уравнением
					x 1 2 y 1 2 16

29.	z x2 xy y 2	1	1
			y
		x


30.	z sin x sin y sin x y , 0 x 2 , 0 y 2 .

31.	u x 2 y 2 2 z y 2 x z 1 2 1

			1			1
			1			1
z					,			33 3
z					,			33 3
	min 3		3		3
			3				3


									3 3
zmax				,
zmax		3		,					2
		3				3			2

	umin 2,					1,		1 1

32. u x2 y 2 z 2 xy x 2z

33. u x3 y 2 z 2 12xy 2z .

34. u x2 y 2 z 2 2x 4 y 6z .

35. u y3 x2 z 2 12xy 2z 13

36. u 5x2 2 y2 2z2 4xy 2 yz 2xz 4x 2 y 3

37. u x2 5y 2 4z 2 2xz 6 yz 8 y 9

38. u x x 2z 2 y 2 2 3 y z 2


39.	u 9x 2 2 y 2 x 2 8y 2z y z 2	2z z 2

40.	u 2 2x2 3 x y 2 2 2 y 4xy 3y 2	4x 6 y 2 z 3z 2

		2			1			4
umin			,			, 1
		3			3			3

umin 24,	144,				1 6913 .
umin 1,			2,				3 14 .
umin 144,		24,			1 6900
umax 1, 1,							1 2
umin 2,					2,		2 1
umin 12, 8,					12 24

umax 1,				2,			2 1


umax 1,			1,			2 3

Убедившись, что точка P( 0,0 ) является стационарной для функции z z( x, y ) , исследовать функцию на локальный экстремум в этой точке z x5 y 4 x4 2 y 2

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1816 17 18 > Следующая >>>