Глава 6

Векторные функции 95

Глава 6. Векторные функции

1 . О п р е д е л е н и е

в е к т о р - ф у н к ц и и с к а л я р н о г о

а р г у м е н т а . Если каждому значению

скалярного аргумента x ставится в соответствие n функций

y1 x , y2 x , ..., yn x , то набор этих функций

называется вектор-функцией y скалярного аргумента

y x y1 x ,

y2 x ,

...,

yn x .

Пусть e1 ,

e2 ,

...,

en - базис

n -мерного векторного пространства. Разложим вектор-функцию по

векторам базиса

y x y1 x e1 y2 x e2

... yn x en .

Если вектор-функцию y x представить как радиус-вектор r x , начало которого поместить в начало

координат, то конец радиус-вектора

r x

будет описывать некоторую кривую, называемую годографом

векторной функции.

2. П р е д е л

и

н е п р е р ы в н о с т ь

в е к т о р - ф у н к ц и и . Вектор a a1 ,

a2 , ..., an называется

0

пределом вектор-функции при x x

lim y x a

, если для любого сколь угодно малого числа 0

x x0

существует такое число 0 , что для всех значений аргумента x

из области 0

x x0

справедливо

неравенство

y x a

.

Вектор-функция

y x называется непрерывной в точке x0

, если

lim y x y x0

.

x x0

3.

П р о и з в о д н а я в е к т о р - ф у н к ц и и с к а л я р н о г о а р г у м е н т а и с в о й с т в а

п р о и з в о д н о й . Производной вектор-функции y x по скалярному аргументу x называется предел

lim

y x0 x y x0

lim

y .

x 0

x

x 0

x

Свойства производной вектор-функции

1.

dy x

y x .

dx

dy x

2. Вектор

лежит на касательной к кривой

dx

dy x

| ( )|

3. y x ,

0 при условии

=const.

dx

4.

( ( ) ( )) (

) (

).

4. О п р е д е л е н и е

ве к т о р - ф у н к ц и и

в е к т о р н о г о

а р г у м е н т а .

Если

каждой

совокупности m переменных x1 ,

x2 ,

...,

xm

соответствует n переменных y1 ,

y2 , ...,

yn так, что

y1 y1 x1 ,x2 ,..., xm ,

y2

y2 x1 ,x2 ,..., xm , ..., yn yn x1 ,x2 ,..., xm ,

то говорят, что задана вектор-функция y y1 ,

y2 ,

...,

yn векторного аргумента x x1 , x2 ,

..., xm

или y x y1 x ,

y2 x ,

...,

yn x , или y y x .

Векторным полем векторной

функции y y x в евклидовом пространстве

R2 называется

совокупность векторов, заданная в каждой точке M x1 ,x2

векторной величиной

y M

y y M y1 x1 ,x2

e1 y2 x1 ,x2 e2

Векторное поле вектора

называется потенциальным, если существует скалярная функция

u M

такая, что grad u y .

Функция u M

называется потенциалом поля,

ее поверхности уровня в

Глава 6

Векторные функции 96

5. П р о и з в о д н а я

в е к т о р - ф у н к ц и и

в е к т о р н о г о

а р г у м е н т а . Производной

dy вектор-

dx

функции y по вектор-аргументу

x в точке x

0 называется предел

lim y x0

x y x0 lim

y .

от y x по

x 0

x

x 0

x

n m ,

Производной

переменной

x является

матрица

Якоби

размерами

составленная

из

частных производных функций

y

y

y

1

1 ...

1

x1

x2

xm

dy

y2

y2

...

y2

dx

x1

x2

xm

.

... ... ... ...

yn

yn

...

yn

x

x

2

x

m

1

Если задана n -мерная дифференцируемая вектор-функция

y от m -мерного вектор-аргумента u , а

вектор-аргумент в свою

очередь является дифференцируемой вектор-функцией от k -мерного вектор-

аргумента x , то

dy u x

dy

du .

dx

du

dx

ПРИМЕР

1.

На

одной

координатной

плоскости

построить

годограф

вектор-функции

y x y

x ,

y

2

x

и ее

вектор-производную

dy x

в заданной точке

1

dx

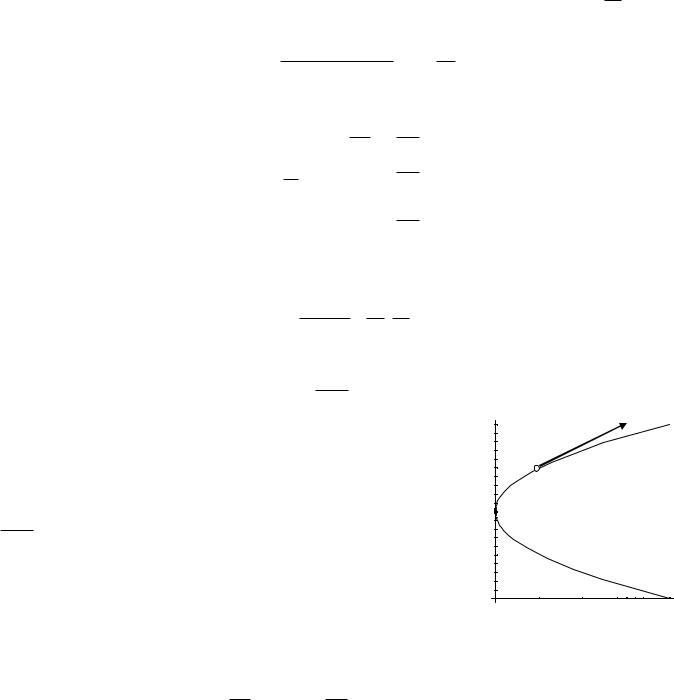
M 1,

3 , если вектор-функция имеет вид

y x x2 ,

x 2 .

4

y2

1

Решение. Выясним, при каком значении x

годограф проходит через

точку M 1,

3 ,

для чего составим и решим систему уравнений

2

1,

.

x

3

x

2

3

М

Ее

решение

x 1.

Найдем

вектор-производную

в

этой

точке

dy x 2x,

1 2,

1 . На рис. 6.1 изображен годограф вектор-функции.

2

dx

2,

1

Вектор-производная представлена вектором с координатами

,

1

касательным к кривой в точке М.

ПРИМЕР 2. Найти потенциал u x ,

x

2

векторного поля

вектора

1

2

3

y

4

grad u 2x1 1 e1 0,5e2

1

1

и

эквипотенциальные

линии

поля

(линии

Рис. 6.1

уровня).

Решение. Наша задача: по известным частным производным

u

2x

1 и

u

0,5

(1)

x1

1

x2

восстановить

потенциал

u x1 ,

x2 .

Подобные

задачи

решаются

методами,

развитыми

в

теории

дифференциальных уравнений. Однако, в простых случаях можно подобрать такую функцию. Например,

u x ,

x

2

x2

x 0,5x

2

. Линии уровня получаются из уравнения x2

x

0,5x

2

c , где c const.

1

1

1

1

1

ПРИМЕР 3. Найти производную сложной

вектор-функции

y u x

по вектор-аргументу x , если

y u1 ,

u2 u1 u2 1,

u1 2u2 ,

u x1 ,

x2 x1 x2 ,

x1 x2 .

Решение. Найдем производные

dy u

и

du x

, которые являются матрицами Якоби

du

dx

dy u

u u

u u

2

1 u

2

1 u

2

1

1

1

1

1

u1

1

2

;

du

2u2 u1

u1 2u2 u2