Vischa_matematika_Chastina_3_Denisyuk_Repeta

1.4.Означення потрійного інтеграла, властивості, геометричний зміст, обчислення.

1.5.Заміна змінних у потрійному інтегралі. Перехід до циліндричних і сферичних координат.

1.6.Застосування потрійних інтегралів.

1.7.Криволінійні інтеграли першого і другого роду. Означення, властивості, обчислення, застосування.

1.8.Формула Гріна.

1.9.Умова незалежності криволінійного інтеграла другого роду від форми шляху інтегрування.

1.10.Обчислення роботи силового поля за допомогою криволінійного інтеграла другого роду.

1.11.Поверхневі інтеграли першого і другого роду. Означення, властивості, зведення до подвійного інтеграла. Застосування.

1.12.Формула Остроградського―Гауcса.

1.13.Скалярне і векторне поля; їх опис за допомогою скалярних і векторних функцій.

1.14.Приклади фізичних скалярних і векторних полів.

Геометричні характеристики поля.

1.15.Лінії і поверхні рівня скалярного поля.

1.16.Векторні лінії векторного поля.

Диференціальні характеристики поля.

1.17.Похідна за напрямом скалярного поля. Градієнт.

1.18.Дивергенція, ротор векторного поля.

1.19.Класифікація векторних полів.

1.20.Оператор Гамільтона.

Інтегральні характеристики поля.

1.21.Потік векторного поля через поверхню.

1.22.Циркуляція векторного поля.

1.23.Формула Остроградського—Гаусса; її векторний запис; фізичний

зміст.

1.24.Формула Стокса; її векторний запис; фізичний зміст.

1.25.Потенціал потенціального поля; його відшукання за допомогою криволінійного інтеграла.

2.Знання на рівні доведень та виведень

2.1.Правило зведення криволінійного інтеграла першого та другого роду до звичайного визначеного інтеграла.

2.2.Правило зведення подвійного інтеграла до повторного.

2.3.Правило зведення поверхневого інтеграла до подвійного.

2.4.Формула Гріна.

111

http://vk.com/studentu_tk, http://studentu.tk/

2.5.Необхідні й достатні умови рівності нулю криволінійного інтеграла по замкненому контуру.

2.6.Формула Остроградського—Гаусса.

2.7.Формула для похідної за напрямом; її вираз через градієнт.

2.8.Властивості градієнта.

3.Уміння в розв’язанні задач

3.1.Зводити подвійний, потрійний, криволінійний і поверхневий інтеграли до визначених інтегралів і обчислювати їх.

3.2.Використовувати при обчисленні кратних інтегралів полярні, циліндричні і сферичні координати.

3.3.Знаходити похідну за напрямом, градієнт, дивергенцію, ротор.

3.4.Визначати тип векторного поля.

3.5.Знаходити потік, роботу, циркуляцію, потенціал.

Тема 1. ПОДВІЙНІ ІНТЕГРАЛИ

Основні поняття та означення. Умови існування та властивості. Обчислення. Заміна змінних у подвійному інтегралі. Застосування.

Література: [3, розділ 2, п. 2.3], [9, розділ 10, §1], [15, розділ 12, п. 12.1], [16, розділ 14, §1—10], [17, розділ 2, §7].

Т.1 ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ

1.1. Задача про об’єм циліндричного тіла

Нехай потрібно обчислити об’єм тіла, обмеженого зверху поверхнею z = f (x, y) , знизу — замкненою обмеженою областю D, що лежить у

площині Оху, з боків — циліндричною поверхнею, напрямна якої збігається з межею області D, а твірні паралельні осі Oz (рис. 2.1). Таке тіло

називають циліндричним. Розіб’ємо область D на n довільних частин Di (i = 1, 2, ..., n), площі яких позначимо через Si . Через межу кожної області Di проведемо прямі, паралельні осі Oz. У результаті тіло поділиться на n частин, його об’єм V дорівнюватиме сумі об’ємів утворених циліндричних стовпців, тобто V = V1 + V2 + …+ Vn , де Vi — об’єм і-го стовпця, обмеженого знизу основою Di , зверху — поверхнею z = f (x, y) , з боків — циліндричною поверхнею, напрямна якої збігається з межею області Di , а

112

http://vk.com/studentu_tk, http://studentu.tk/

твірні паралельні осі Oz. Візьмемо в кожній області Di довільну точку Mi (xi , yi ) , обчислимо значення функції f (xi , yi ) і розглянемо добуток f (xi , yi ) Si . Цей добуток визначає об’єм циліндричного стовпчика з основою Di і висотою f (xi , yi ) , який наближено дорівнює об’єму Vi .

Отже, справедлива наближена формула

n

V ≈ ∑ f (xi , yi ) Si .

i=1

Із збільшення числа n областей Di і одночасним зменшенням розміру

кожної області Di наближення стає точнішим. Нехай λ = max di — най-

i

більший з діаметрів областей Di (діаметр — найбільша відстань між точками області) прямує до нуля. У цьому разі число областей Di , кожна з

яких стягується у точку, необмежено зростає. Тоді об’єм даного тіла визначається граничною формулою

1.2. Означення подвійного інтеграла

Нехай функція z = f (x, y) визначена і неперервна в замкненій обмеженій області D площини Oxy (рис. 2.2). Розіб’ємо область D на n довільних частин Di (i = 1, 2,..., n) , площі яких позначимо через Si . Візьмемо в кожній області Di довільну точку Mi (xi , yi ) , обчислимо значення функції f (xi , yi ) й утворимо суму

нуля). Якщо ця границя існує і не залежить ні від способу розбиття області

http://vk.com/studentu_tk, http://studentu.tk/

Отже, за означенням

У цьому разі функцію f (x, y) називають інтегровною в області D; D — областю інтегрування; x, y — змінними інтегрування; dxdy (або dS ) — елементом площі.

z

z = f(x, y)

f(xi , yi )

Теорема (достатня умова інтегровності функції). Якщо функція f (x, y) неперервна в замкненій обмеженій області D, то

вона інтегровна в цій області.

1.3. Геометричний зміст подвійного інтеграла

Порівнюючи означення подвійного інтеграла із формулою (2.1) для обчислення об’єму циліндричного тіла, доходимо висновку, що геометрично подвійний інтеграл виражає об’єм циліндричного тіла, обмеженого

зверху поверхнею z = f (x, y) , де f (x, y) ≥ 0 , знизу — замкненою обмеже-

ною областю D, з боків — циліндричною поверхнею, напрямна якої збігається з межею області D, а твірні паралельні осі Oz .

Отже, об’єм циліндричного тіла обчислюють за формулою

V = ∫∫ f (x, y)dxdy.

D

Якщо для всіх точок області D функція f (x, y) ≡ 1 , то об’єм циліндричного тіла чисельно дорівнює площі основи D, тобто

S = ∫∫ dxdy.

D

114

http://vk.com/studentu_tk, http://studentu.tk/

1.4. Властивості подвійного інтеграла

Порівнюючи означення подвійного та визначеного інтегралів, дійдемо висновку, що ці інтеграли будуються за однаковою схемою. Звідси випливає, що і властивості подвійного інтеграла аналогічні властивостям визначеного інтеграла. Сформулюємо ці властивості без доведення.

Нехай підінтегральні функції наступних інтегралів інтегровні. 1) сталий множник можна винести за знак подвійного інтеграла:

∫∫ Cf (x, y)dxdy = C∫∫ f (x, y)dxdy , С— стала;

D D

2) подвійний інтеграл від суми (різниці) двох функцій дорівнює сумі (різниці) подвійних інтегралів від цих функцій:

∫∫( f (x, y) ± g(x, y))dxdy =∫∫ f (x, y)dxdy ±∫∫ g(x, y)dxdy;

D D D

3)якщо в області D f (x, y) ≥ 0 , то

∫∫f (x, y)dxdy ≥ 0;

D

4)якщо f (x, y) ≤ g(x, y) для всіх точок області D, тоді

∫∫f (x, y)dxdy ≤∫∫ g(x, y)dxdy;

DD

5)якщо область D розбити на дві частини D1 та D2 , які не мають спільних внутрішніх точок, то

6) (про оцінку подвійного інтеграла). Якщо функція f (x, y) неперер-

вна в області D, S — площа області D, m i M — відповідно найменше і найбільше значення функції f (x, y) в області D, то

mS ≤ ∫∫ f (x, y)dxdy ≤ MS;

D

7) (Про середнє значення функції). Якщо функція f (x, y) неперервна в

замкненій обмеженій області D з площею S, то в цій області існує точка (x0 , y0 ) така, що

∫∫ f (x, y)dxdy = f (x0 , y0 ) S.

D

115

http://vk.com/studentu_tk, http://studentu.tk/

При цьому величину

f (x0 , y0 ) = S1 ∫∫D f (x, y)dxdy

називають середнім значенням функції f (x, y) в області D.

1.5. Обчислення подвійного інтеграла

Розглянемо спочатку випадок обчислення подвійного інтеграла в прямокутних декартових координатах. Покажемо, що його обчислення зводиться до послідовного обчислення двох визначених інтегралів.

Нехай потрібно обчислити подвійний інтеграл

∫∫ f ( x, y) dxdy ,

D

де f (x, y) — невід’ємна і неперервна в області D функція. Згідно з геомет-

ричним змістом подвійного інтеграла значення цього інтеграла чисельно дорівнює об’єму циліндричного тіла з основою D, обмеженого зверху

поверхнею z = f (x, y) (рис. 2.3). Обчислимо об’єм, використовуючи метод паралельнихперерізів. Зацимметодомоб’ємтілаобчислюютьзаформулою

a

де S(x) — площа поперечного перерізу тіла площиною, перпендикулярною

доосі Ох, x = a та x = b — рівняння площин, які обмежують дане тіло. Накладемо на форму області D деякі обмеження. Нехай область інте-

грування D обмежена неперервними кривими y = ϕ1 (x) , y = ϕ2 (x) та пря-

мими x = a та x = b , причому a < b , ϕ1 (x) ≤ ϕ2 (x) для всіх x [a; b] (рис. 2.4). У цьому разі будь-яка пряма, яка паралельна осі Oу і проходить

через точку (х; 0), де x (a; b) , перетинає межу області D не більше ніж у двох точках. Таку область називають правильною у напрямку осі Oу.

Проведемо площину x = const , деx (a; b) , перпендикулярну до осі Ох.

Переріз цієї площини з циліндричним тілом — криволінійна трапеція АВСК,

обмежена кривою z = f (x, y) , x = const , прямими — y = ϕ1 (x), y = ϕ2 (x) та z = 0. Площу трапеції визначаємо за формулою

ϕ 2 ( x)

S(x) = ∫ f (x, y)dy .

ϕ1 ( x)

116

http://vk.com/studentu_tk, http://studentu.tk/

Після цього формула (2.3) набирає вигляду

z

z = f(x, y)

Рис. 2.3` Рис. 2.4

Схематично обчислення подвійного інтеграла відбувається у такій послідовності:

У повторному інтегралі (2.4) інтегрування спочатку виконується за змінною y (внутрішній інтеграл, при цьому змінна x вважається сталою).

У результаті обчислення внутрішнього інтеграла (в межах від ϕ1 (x) до ϕ2 (x) ) одержуємо певну функцію від однієї змінної x . Інтегруючи цю

область є правильною у напрямку осі Ох, тобто будь-яка пряма, яка паралельна осі Oх і проходить через точку (0; у), де y (c; d ) , перетинає межу області D не більше ніж у двох точках.

117

http://vk.com/studentu_tk, http://studentu.tk/

У цьому разі подвійний інтеграл обчислюють за формулою

Зауваження

1.Якщо область інтегрування правильна і в напрямку осі Оу, і в напрямку осі Ох (таку область називатимемо правильною), тоді інтегрування можна проводити як за формулою (2.4), так і за формулою (2.5). На вибір порядку інтегрування впливає форма області D, яка визначається рівняннями межі цієї області.

2.Якщо область D правильна, наприклад у напрямку осі Оу, а межа цієї

області задається кривими y = ϕ1 (x) , y = ϕ2 (x) , y = ϕ3 (x) та прямими x = a , x = b (рис. 2.6), то в цьому разі подвійний інтеграл дорівнює сумі двох повторних інтегралів

набувають найпростішого вигляду

118

http://vk.com/studentu_tk, http://studentu.tk/

рала таку область необхідно розбити на частини, кожна з яких правильна хоча б в одному напрямі. Так, розбиття області D, зображене на рис. 2.8, б, даєможливістьскористатисяформулою(2.4), анарис. 2.8, в―формулою(2.5).

Для спрощення обчислень подвійного інтеграла ∫∫ f (x, y)dxdy , де

D

f (x, y) ― неперервна в області D, інколи переходять від прямокутних

декартових координат х і у до нових криволінійних координат u і v. Нехай нові змінні u і v пов’язані з прямокутними координатами х і у

співвідношеннями x = x(u, v) , y = y(u, v) , де функції x(u, v) та y(u, v) , які

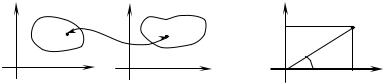
неперервні разом із своїми частинними похідними першого порядку, встановлюють взаємно однозначну відповідність між точками області D площини Оху і точками області D′ площини O′uv (рис. 2.9) і, крім того,

визначник перетворення (визначник Якобі або якобіан) в області D′ не обертається у нуль:

119

http://vk.com/studentu_tk, http://studentu.tk/

Тоді справедлива формула заміни змінних у подвійному інтегралі:

Розглянемо частинний випадок заміни змінних, а саме перехід у подвійному інтегралі до полярних координат.

Вважатимемо зановізмінні полярні координати ρ і ϕ , які пов’язані з декартовими координатами х та у формулами x = ρcos ϕ, y = ρ sin ϕ (рис. 2.10). Тоді

де D1 — область, яка відповідає області D у полярній системі координат. У полярній системі координат за незалежну змінну вибирають ϕ , а ρ

розглядають як функцію від ϕ , тобто ρ = ρ(ϕ) (α ≤ ϕ ≤ β) .

Подальше зведення подвійного інтеграла до повторного інтеграла залежить від області інтегрування. Розглянемо найтиповіші випадки:

формулу (2.7) можна записати у вигляді

120

http://vk.com/studentu_tk, http://studentu.tk/