Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Vischa_matematika_Chastina_3_Denisyuk_Repeta

.pdf

Скачиваний:

410

Добавлен:

19.02.2016

Размер:

7.52 Mб

Скачать

☆

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 4518 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

Зокрема:

а) якщо просторова крива задана рівняннями x = x(t), y = y(t), z = z(t), t [α, β] , то

L = ∫ (x′(t))2 + ( y′(t))2 + (z′(t))2 dt;

б) якщо плоска крива задана рівнянням y = y(x) , x [а; b], тоді

′

dx.

(2.32)

L = ∫ 1+ ( y (x))

Площу Р циліндричної поверхні, визначеної невід’ємною функцією

z = f (x, y) , напрямною АВ у площині Оху,

а твірні поверхні паралельні осі

Оz, визначають за формулою

P = ∫

f (x, y)dl.

(2.33)

Масу m кривої L обчислюють за формулою

m = ∫ γ(x, y)dl,

де γ (x, y) — лінійна густина матеріальної кривої у точці M (x,

y) .

Координати xc ,

yc центра маси кривої L знаходять за формулами

∫ xγ (x, y)dl

∫ yγ (x, y)dl

(2.34)

= L

, y

= L

Площу S плоскої фігури, розміщеної у площині Оху і обмеженої

замкненим контуром L, обчислюють за формулою

S =

∫ xdy − ydx.

(2.35)

Роботу сили F = P(x, y, z)i + Q(x, y, z) j + R(x, y, z)k

(функції P(x, y, z),

Q(x, y, z), R(x, y, z) неперервні на просторовій кривій L) при переміщенні матеріальної точки вздовж кривої L визначають за формулою

171

http://vk.com/studentu_tk, http://studentu.tk/

A = ∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz.

Зокрема, якщо крива L лежить у площині Оху, тоді сила F = P(x, y)i +

+Q(x, y) j при переміщенні матеріальної точки вздовж кривої L виконує роботу

		A = ∫ P(x, y)dx + Q(x, y)dy.	(2.36)
		L
		ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
	Т.3	ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
1. Обчисліть криволінійні інтеграли першого роду:
а) ∫ xdl,		де AB — дуга параболи y = x2 від точки А (0; 0) до точки

B (1; 1) (рис. 2.47);

б) ∫ x2 ydl , де L — дуга кола x2 + y2 = 1 , розміщена у першій чверті

(рис. 2.48).

Розв’язання: а) Знаходимо y′ = 2x і за формулою (2.23) дістаємо

			1				1	1
	∫		xdl = ∫ x			1+ 4x2 dx =	1	∫		1+ 4x2 d(1+ 4x2 ) =
	∫		xdl = ∫ x			1+ 4x2 dx =	8	∫		1+ 4x2 d(1+ 4x2 ) =
	AB		0				8	0
	AB		0					0
			=	1		(1+ 4x2 )3	1	=		1	(5 5 −1).
							1

				12			0		12
				12			0		12
б)	Параметризуємо дугу L: x = cos t,									y = sin t,			0 ≤ t ≤		π	. Тоді за фор-
мулою (2.25) маємо															2
мулою (2.25) маємо
	π									π								3		π
	2								2								cos	3	t	2		1
∫ x2 ydl = ∫ cos2 t sin t					sin2 t + cos2 tdt			= − ∫ cos2 td(cos t) = −									cos		t	2	=	1	.
∫ x2 ydl = ∫ cos2 t sin t					sin2 t + cos2 tdt			= − ∫ cos2 td(cos t) = −													=		.
L	0								0							3				0		3
L	0								0											0
	у										у
	1				В						1	В	L
	1				В						1		L
	А					х					О			А		х

			1										1
		Рис. 2.47									Рис. 2.48
172

http://vk.com/studentu_tk, http://studentu.tk/

2. Визначте масу гвинтової лінії	x = 3cost,	y = 3sin t,
z = 4t, 0 ≤ t ≤ 2π (рис. 2.49), якщо	густина в	кожній її

точці (x, y, z) визначаєтьсязаформулою γ (x, y, z) = 2z.

Розв’язання. Масу заданої просторової кривої визначимо за формулою

m = ∫ γ(x(t), y(t), z(t)) (x′(t))2 + ( y′(t))2 + (z′(t))2 dt.

Оскількиγ(x, y, z) =	2z = 2 4t = 8t ,		′
		x (t) = −3sin t,
z′(t) = 4 , y′(t) = 3cos t, то
2π				2π
m = ∫ 8t 9 sin2 t +	9 cos2 t + 16dt = 20t2				= 80π2 .
				0
0

8π

3 у

x 3

Рис. 2.49

3. Знайдіть координати центра маси однорідної дуги

ланцюгової лінії y =	ex + e− x	, 0	≤ x ≤ ln 2 (рис. 2.50).
	2

Розв’язання. Оскільки центр маси однорідної дуги не залежить від значення густини, то вважатимемо її рівною одиниці. Тоді маса дуги чисельно дорівнюватиме довжині цієї дуги. Враховуючи, що

Оln2 х

Рис. 2.50

1+ ( y′)2 = 1+	1	(ex − e− x )2	=	1	(ex + e− x )2 =	1	(ex + e− x ),
	4			2		2

за формулою (2.32) дістаємо

									1	ln 2						1			ln 2			3
										ln 2									ln 2
				L = m =						∫ (ex + e− x )dx =							(ex − e− x )		=				.
				L = m =						∫ (ex + e− x )dx =							(ex − e− x )		=			4	.
								2		0			2						0			4
										0									0
Тепер за формулами (2.34) знаходимо
x =	4	ln 2 x				1+		( y′(x))2 dx =			2	ln 2 (x(e x +e− x ))dx =								2	x(e x −e− x )					ln 2 −
	4										2									2
	3																		3
c	3	∫									3 ∫								3							0
c		0										0														0
			2			ln 2							2					ln 2						1
						ln 2												ln 2
		−					∫ (e x −e− x )dx = ln 2 −								(e x		+e− x )		= ln 2			−			;
		−	3				∫ (e x −e− x )dx = ln 2 −						3		(e x		+e− x )	0	= ln 2			−		3	;
			3			0							3					0						3
					4 ln 2					′	2			4 ln 2 ex + e− x ex + e− x
							∫								∫
	yc =				3		∫	y 1+ ( y (x)) dx =						3	∫		2		2					dx =
	yc =					0		y 1+ ( y (x)) dx =					0											dx =
						0							0

173

http://vk.com/studentu_tk, http://studentu.tk/

	1	ln 2							1			1				1		ln 2
=	1	∫ (e2x		+ 2 + e−2x )dx =					1		(	1	e2x + 2x −			1	e−2x )		=
=	3	∫ (e2x		+ 2 + e−2x )dx =				3			(	2	e2x + 2x −			2	e−2x )	0	=
	3	0						3				2				2		0
		=	1	1	4 + 2 ln 2	−	1			1			=	1	(16 ln 2		+ 15).

			3	2			2			4				24
			3	2			2			4				24
4. Обчисліть криволінійний інтеграл першого роду ∫																			x2 + y2 dl , де
																		L

L — верхня половина кардіоїди ρ = 1+ cos ϕ (рис. 2.51).

уРозв’язання. Перейдемо до полярних координат за

то

174

формулами x = ρ cos ϕ ,

y = ρ sin ϕ , тоді

x2 + y2 = ρ.

Оскільки

ρ′ = − sin ϕ ,

ρ2 + (ρ′)2 = (1+ cos ϕ)2 + sin2 ϕ = 2

+ 2 cos ϕ = 4 cos2 ϕ ,

Рис. 2.51

′ 2

для ϕ [0; π] ,

+ (ρ )

= 2

cos

= 2 cos 2

ϕdϕ =

∫ x2 + y2 dl = ∫ ρ 2 cos

∫ (1+ cos ϕ) 2 cos ϕdϕ =

2 cos

4 cos

− sin

= ∫

= 8∫

d sin

3 ϕ

= 8

sin

−

sin

= 8

1−

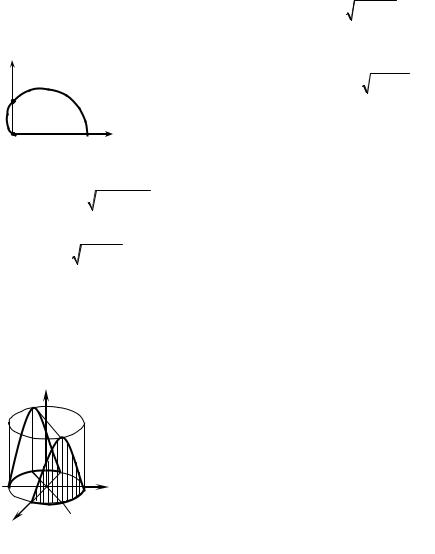
5. Обчисліть площу бічної поверхні

кругового

циліндра

x2 + y2

= 4 ,

зрізаного

знизу

площиною

2 y

2	у = х

Оху,	а зверху — гіперболічним параболоїдом
z = xy	(рис. 2.52).

Розв’язання. Виходячи з геометричного змісту криволінійного інтеграла першого роду, задачу зводимо до обчислення криволінійного інтеграла від

функції f (x, y) = xy ( f (x, y) ≥ 0)	вздовжкола x2 + y2 = 4
(формула (2.33)). Оскільки	f (x; y) ≥ 0 при x ≥ 0,

Рис. 2.52

y ≥ 0 і x ≤ 0, y ≤ 0 , а поверхня z = xy симетрична

http://vk.com/studentu_tk, http://studentu.tk/

відносно площини y = x , то можна обмежитися обчисленням інтеграла

лише вздовж четвертої частини кола, що міститься у першій чверті площини Оху, і результат подвоїти. Дістанемо

y = 4 − x2 , y′ = −

4 − x2

1+ ( y′)2 =

, dl =

1+ ( y′)2 dx =

2dx

− x2

4 − x2

2 = 8.

P = ∫ f (x, y)dl = 2∫ x 4 − x2

dx = 2 x2

4 − x2

6. Обчисліть криволінійні інтеграли другого роду:

а) ∫ x2 dx + xydy , якщо АВ — відрізок, що з’єднує точки А(1; 1) і В(2; 3)

(рис. 2.53);

б) ∫ (x − y)dx + (x + y)dy , якщо L — ламана ОАВ, де O(0; 0), A(2; 0), В(2; 3)

(рис. 2.54);

в) ∫ xdx + y2 dy , якщо AB — дуга параболи					y = x2 від точки А(0; 0) до
AB
точки В(2; 4) (рис. 2.55);
г) ∫	dx	−	dy	, якщо L — перша чверть кола x2	+ y2 = 4 (обхід здійсню-

L y			x
ється за годинниковою стрілкою).

Розв’язання: а) Запишемо рівняння прямої, що проходить через точки

А(1; 1) і В(2; 3):	x − 1	=	y − 1	, тобто y = 2x − 1. Рівняння	відрізка АВ:
А(1; 1) і В(2; 3):	2 − 1	=	3 − 1	, тобто y = 2x − 1. Рівняння	відрізка АВ:
	2 − 1		3 − 1
y = 2x − 1, 1 ≤ x ≤ 2 . Тепер за формулою (2.28) дістаємо
		2		2		26
∫ x2 dx + xydy = ∫ (x2 + x(2x − 1) 2)dx = ∫ (5x2 − 2x)dx =						26	.
∫ x2 dx + xydy = ∫ (x2 + x(2x − 1) 2)dx = ∫ (5x2 − 2x)dx =					3		.
AB		1		1	3
AB		1		1

б) Запишемо інтеграл у вигляді суми двох інтегралів, перший з яких візьмемо вздовж відрізка ОА, а другий — вздовж відрізка АВ. На відрізку

ОА y = 0, dy = 0, 0 ≤ x ≤ 2, тому

175

http://vk.com/studentu_tk, http://studentu.tk/

∫ (x − y)dx + (x + y)dy = ∫ xdx = 2.

На відрізку AB x = 2 ,

dx = 0 ,

0 ≤ y ≤ 3 , значить,

∫

(x − y)dx

+ (x + y)dy =

(2 + y)dy = 2 y +

= 6

= 10, 5.

Отже,

∫ (x − y)dx + (x + y)dy = 2 + 10, 5 = 12, 5.

1	А					А
			х			А			х
О	1	2	х	О	2	х	А	2	х

Рис. 2.53

Рис. 2.54

Рис. 2.55

в) Маємо (див. рис. 2.55):

∫ xdx + y2 dy = ∫ xdx + ∫

y2 dy = ∫ xdx + ∫ y2 dy =

г) Запишемо рівняння заданої дуги кола у параметричній формі: x = 2cost,

y = 2sin t, 0 ≤ t ≤

π . Тоді

x′(t) = −2 sin t, y′(t) = 2 cos t і за формулою (2.27)

дістаємо

2 sin t

2 cos t

∫

∫ dt = 2∫ dt = π .

−

dt = −2

2 sin t

2 cos t

7. Обчисліть площу області, обмеженої еліпсом

= 1.

Розв’язання.

Запишемо рівняння

еліпса у

параметричному вигляді:

x = a cos t,

y = b sin t,

t [0; 2π] . Для обчислення площі застосуємо фор-

мулу (2.35). Тоді

176

http://vk.com/studentu_tk, http://studentu.tk/

2π

S =

∫ xdy − ydx =

∫ (a cos t b cos t − b sin t a sin t)dt =

2π

∫ (cos2 t + sin2 t)dt =

∫ dt = πab.

8. Обчисліть криволінійний інтеграл

I = ∫ (x2 + y2 )dx + xdy за форму-

лою Гріна, якщо L ― трикутник з вершинами О (0; 0), А(1; 0), В(0; 1)

(рис. 2.56).

∂Q

− ∂P =

Розв’язання. Маємо

P = x2 + y2 , Q = x,

= 1− 2 y. За формулою (2.30) дістаємо

∂x

∂y

х + у = 1

∫ (x2 + y2 )dx + xdy = ∫∫ (1− 2 y)dxdy,

де область D — трикутник ОАВ. Оскільки рівняння

Рис. 2.56

сторони АВ має вигляд х + у = 1, то

1 1− x	1
I = ∫∫ (1− 2 y)dxdy = ∫ dx ∫	(1− 2 y)dy = ∫ ( y − y2 )

D			0 0
	1
	∫		(1− x)2 )dx =
=		(1− x −	(1− x)2 )dx =	−
	0
		(1;2)
9. Обчисліть I = ∫			(x2 + y)dx + (x

			0
(1	− x)2		(1	− x)3	1
(1	− x)2		(1	− x)3	1
		+
		+
	2			3	0
	2			3	0

+ 2 y)dy.

(0;0)

1− x

dx =

= 16 .

Розв’язання. Перевіримо умову незалежності криволінійного інтеграла

від форми шляху інтегрування: P = x2 + y , Q = x + 2 y , ∂P

∂y

Отже, умова (2.31) виконується, тому значення інтеграла не залежить від шляху інтегрування. Будемо рухатись від точки (0; 0) до точки (1; 2) вздовж ламаної ОАВ

(рис. 2.57). Маємо на ОА: у = 0, dy = 0, 0 ≤ x ≤ 1; на АВ: х = 1, dx = 0, 0 ≤ y ≤ 2 . Отже,

1		2		x	3	1			2		19			1

I = ∫ x	2	dx + ∫ (1	+ 2y)dy =			+ ( y + y	2	)		=			= 6		.
				3					0			3		3
0		0				0

= ∂∂Qx = 1 .

2 В

		А
О	1	х

Рис. 2.57

177

http://vk.com/studentu_tk, http://studentu.tk/

10. Обчисліть роботу, яку виконує сила F = y2 i + x j при переміщенні матеріальної точки вздовж прямої, що сполучає точки А(1; 2) та В(2; 4).

	Розв’язання. Потрібно обчислити криволінійний інтеграл другого роду
від функцій P = y2									і Q = x вздовж відрізка АВ. Складемо рівняння відрізка
АВ:		x −1	=	y − 2	,		звідси y = 2x . За формулою (2.36) маємо
АВ:			=		,		звідси y = 2x . За формулою (2.36) маємо
		2 − 1		4 − 2
																					2		4		y
				A = ∫		y2 dx + xdy = ∫										y2 dx + ∫			xdy = ∫			4x2 dx + ∫			y	dy =
				A = ∫		y2 dx + xdy = ∫										y2 dx + ∫			xdy = ∫			4x2 dx + ∫		2		dy =
				AB										AB				AB			1		2	2
				AB										AB				AB			1		2
				=				4	x	3	2	+	y2		4	=	4	(8 −1)	+	1	(16	− 4) =	37	.
								4		3	2		y2		4		4			1			37
							3				1		4		2		3			4			3
							3				1		4		2		3			4			3

11.Обчисліть криволінійний інтеграл

∫(x3 + 2xy)dx + (x2 − cos y)dy ,

якщо L ― еліпс x2 + 4 y2

= 4 .

Розв’язання. Оскільки

∂P

∂(x3

2xy)

= 2x ,

∂Q

∂(x2 − cos y)

= 2x , то

∂y

∂x

∂P

= ∂Q ікриволінійний інтегралпозамкненомуконтуруL дорівнює нулю.

∂y

∂x

12. Обчисліть криволінійний інтеграл

I = ∫ (x2 + 2z)dx + (x − y)dy + (x + 2z)dz ,

якщо L ― відрізок, що сполучає точки A (2; 0; − 1) та B(4; 1; 2) .

Розв’язання. Складемо параметричні рівняння прямої АВ:

x − 2

y − 0

z + 1

x − 2

= y =

z + 1

= t ,

4 − 2

1− 0 2 + 1

x = 2t + 2, y = t, z = 3t − 1 — параметричні рівняння прямої АВ.

Точку А дістаємо з параметричних рівнянь при

t = 0 ; точці В відпо-

відає значення t = 1. Отже, на відрізку АВ t [0; 1] .

178

http://vk.com/studentu_tk, http://studentu.tk/

Враховуючи, що dx = 2dt, dy = dt,

dz = 3dt, обчислюємо криволінійний

інтеграл

I = ∫ (((2t + 2)2 + 2(3t − 1)) 2 + (2t + 2 − t) + (2t + 2 + 2(3t − 1)) 3)dt =

= ∫

(8t

+ 53t +

6)dt =

+ 6 = 35

ВПРАВИ ДЛЯ АУДИТОРНОЇ

Т.3

І САМОСТІЙНОЇ РОБОТИ

Обчисліть криволінійні інтеграли першого роду.

∫ sin3 x cos xdl , якщо L — дуга кривої y = ln sin x , x [π / 6; π / 2].

∫ y2 dl , якщоL — аркациклоїди x = t − sin t,

y = 1− cos t ( 0 ≤ t ≤ 2π ).

∫

, якщо L — відрізок, що сполучає точки А(–2; 0) та В(4; 0).

− y

∫ xy−4dl, якщоL — дугагіперболи xy = 1 міжточкамиА(1; 1) таВ(2; 1/2).

∫

x2 + y2 dl , якщо L — коло x2 + y2

= 2x .

∫

x2 + y2 + 1dl , якщо L — дуга спіралі Архімеда ρ = ϕ між точками

А(0; 0) та В(1; 1).

∫ xy2 dl , якщо L — дуга кола x = R cos t,

y = R sin t

( 0 ≤ t ≤ π / 2 ).

∫ (x2 + y2 + z2 )dl , якщо L — дуга гвинтової лінії

x = cos t,

y = sin t,

≤ t ≤ 2π ).

z = bt ( 0

∫ (2x − 3y + z + 4)dl , якщо L — відрізок, що сполучає точки А(1; 3; –1)

та В(2; 0; 3).

Обчисліть криволінійні інтеграли другого роду.

10. ∫

x2 + 8ydx − (xy + 1)dy,

якщо L — дуга параболи y = x2

між точ-

ками А(0; 0) та В(2; 4).

179

http://vk.com/studentu_tk, http://studentu.tk/

11.	∫ xdy − ydx, якщо L — дуга астроїди x = 2cos3 t, y = 2sin3 t,			0 ≤ t ≤ π / 2.
	L
12.	∫ y cos3 xdx + y−2 dy, якщо L — дуга кривої y = tg x ,		π ≤ x ≤ π .
	L		4	3
	L
13.	∫ y2 dx + x2 dy, якщо L	— перша арка циклоїди	x = a(t − sin t),
	L
y = a(1− cos t).
14. ∫ xydx + zdy + (x2 + y2 )dz,		якщо L — дуга гвинтової лінії		x = a cos t,
	L
y = a sin t, z = bt ( 0 ≤ t ≤ π ).
15.	∫ (x − 1)dx + (x − y)dy + (2z − x)dz, якщо L — відрізок, що сполучає
	L
точки А(0; 0; 0) та В(1; 2; 3).
16.	∫ (x2 − y)dx + ( y2 + 2x)dy, якщо L — ламана, що послідовно спо-
	L

лучає точки А(0; 0), В(1; 1), С(1; 0) та D(3; 0).

Обчисліть криволінійні інтеграли другого роду, використовуючи формулу Гріна.

17.	∫ 2xdy − ydx, якщо L — замкнений контур, утворений частинами
	L
параболи y = x2 та прямої y = x .
18.	∫ (1− x2 ) ydx + (1+ y2 )xdy, якщо L — коло x2 + y2 = R2 .
	L
19.	∫ (xy + x + y)dx + (xy + x − y)dy, якщо L — коло x2 + y2 = 2x.
	L
20.	∫ xydx + (x2 + y2 )dy, якщо L — контур трикутника з вершинами в
	L

точках А(1; 0), В(2; 1) та С(1; 2).

21. Визначте координати центра маси однорідної дуги циклоїди

x= a(t − sin t), y = a(1− cos t), 0 ≤ t ≤ 2π.

22.Обчисліть роботу сили F = {x; y} при переміщенні матеріальної точки вздовж кривої y = t cos t − sin t , x = t sin t + cos t , t [0; π / 2] .

23.Обчисліть роботу сили F = {yx; yz; xz} при переміщенні матеріальної точки по відрізку, що сполучає точки А(0; 1; 1) та В(2; –1; 3).

180

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 4518 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2019882.69 Кб33Vikova_psikhol_Konsp_Alp.doc
#
19.02.2016908.69 Кб55Vischa_geodeziya.docx
#
19.02.20168.29 Mб315Vischa_matematika_Chastina_1_Denisyuk_Repeta.pdf
#
19.02.20164.86 Mб918Vischa_matematika_Chastina_2_Denisyuk_Repeta.pdf
#
19.02.20162.32 Mб223Vischa_matematika_Chastina_2_Denisyuk_Repeta.pdf
#
19.02.20167.52 Mб410Vischa_matematika_Chastina_3_Denisyuk_Repeta.pdf
#
19.02.20161.68 Mб74Vitorskaya_N_Prichiny_Bolezn_Istoki_Zdorov_Pra.doc
#
26.08.201978.26 Кб0voprosy_1-10.docx
#
19.02.201650.69 Кб79Voprosy_na_ekzamen_TS.doc
#
19.02.20161.5 Mб8vsesvitny_istoria_shupak1-39.pdf
#
09.12.2018260.17 Кб18vse_gotovo.docx