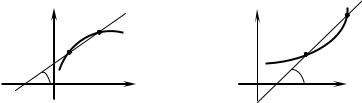Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Vischa_matematika_Chastina_3_Denisyuk_Repeta

.pdf

Скачиваний:

414

Добавлен:

19.02.2016

Размер:

7.52 Mб

Скачать

☆

<<< < Предыдущая 16 17 18 19 20 21 22 23 24 25 26 2728 / 4528 29 30 31 32 33 34 35 36 37 38 39 40 > Следующая >>>

3+i

1.5.25. а)

4 ;

б) sh (–1 – 2i);

в) Arccos (4i) .

1.5.26. а) 6−i ;

б) сh (1–3і);

в) Arccos3i .

1.5.27. а) (i + 1)i ;

б) th (2–3і);

в)

cos (

8π

+ 2i) .

1.5.28. а)

cos(4 + i);

б)

Ln(2 3 − 2i) ;

в)

ctg

i .

1.5.29. а)

ctg πi;

б)

(1− 3i)i ;

в) Arccos (−3i) .

1.5.30. а)

Ln(1− 3i) ;

б)

(1−

3i)−i ;

в)

cos (

13π

+ i) .

1.6. Виділіть дійсну та уявну частини функцій.

1.6.1. f(z) = e–z.

1.6.2. f(z) = sin 3z.

1.6.3. f(z) = ez2 .

1.6.4. f(z) = sin3z sin z.

1.6.5. f(z) = cos 4z.

1.6.6. f(z) = zln z.

1.6.7. f(z) = zez.

1.6.8. f(z) = z2cos z.

1.6.9. f(z) = z2sin z.

1.6.10. f(z) = Ln z.

1.6.11. f(z) = sh (z + 2i).

1.6.12. f(z) = z3ln z.

1.6.13. f(z) =

(2 + i)z2 − 3z .

1.6.14. f(z) = ez 2 .

1.6.15. f(z) = (2 − i)z2 .

1.6.16. f(z) = (1+ i)z3 .

1.6.17. f(z) = z sin z.

1.6.18. f(z) = z cos z.

1.6.19. f(z) = z2ez.

1.6.20. f(z) = cos (z+i).

1.6.21. f(z) =

1.6.22. f(z) =

1.6.23. f(z) = 2z2 +3z – 4iz.

1.6.25. f(z) = z . z2

1.6.27. f(z) = Re(sin z)cos z.

1.6.29. f(z) = cth z.

ez + 1

1.6.24. f(z) = ez − 1 .

1.6.26. f(z)= e− z . z

1.6.28. f(z) = Re(cos z)sin z. 1.6.30. f(z) = z (Re z + iIm z2).

271

http://vk.com/studentu_tk, http://studentu.tk/

Тема 2. ДИФЕРЕНЦІЮВАННЯ ТА ІНТЕГРУВАННЯ

ФУНКЦІЇ КОМПЛЕКСНОЇ ЗМІННОЇ

Диференційовність, аналітичність функції. Умови Коші—Рі- мана. Гармонічні функції. Інтегрування функції комплексної змінної. Інтегральна теорема Коші. Інтегральна формула Коші. Формула Ньютона—Лейбніца.

Література: [4, розділ 1, пп.1.4—1.6], [5, гл.1, пп.1.4—1.6], [12, розділ 30, §1—3], [13, розділ 1, §3—5], [15, розділ 15, п. 15.2], [17, розділ 8, §28—29].

Т.2 ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ

2.1.Диференціювання функції комплексної змінної. Умови Коші—Рімана. Гармонічні функції

Нехай однозначна функція w = f(z) визначена в області D і нехай точка z належить цій області. Похідною f ′(z) у точці z називають границю відно-

шення приросту функції f(z) у точці z до приросту аргументу ∆z, коли приріст аргументу прямує до нуля, тобто

f ′(z) = lim	f (z)	= lim	f (z +	z) − f (z)	.
	z
z→0		z→0		z

Функцію f(z), яка має в точці z D скінченну похідну f ′(z) , називають

диференційовною в цій точці. Функцію, диференційовну в кожній точці області, називають диференційовною в цій області.

Теорема 1

Якщо функція f (z) = u(x, y) + iυ( x,

y) визначена в деякому

околі точки z = x + iy ,

причому в цій точці дійсні функції

u(x, y)

та υ( x, y) диференційовні,

то для диференційовності функції

w = f (z)

у точці z = x + iy необхідно і достатньо, щоб у цій точці викону-

вались рівності (умови Коші—Рімана):

∂u

∂v

∂u

= −

∂v

(3.8)

∂x

∂y

∂x

Якщо виконано всі умови теореми, то похідну диференційовної функції f (z) можна обчислити за однією з формул:

272

http://vk.com/studentu_tk, http://studentu.tk/

f ′ (z) =

∂u

+ i

∂v

− i

∂u

− i

∂u

∂v

+ i

∂v .

(3.9)

∂x

∂y

∂x

∂y

∂x

Одне з найважливіших понять у теорії функції комплексної змінної ― поняття аналітичної функції.

Однозначну функцію f(z) називають аналітичною в точці z, якщо вона диференційовна (виконуються умови Коші—Рімана) в деякому околі цієї точки. Функцію f(z) називають аналітичною в області D, якщо вона диференційовна в кожній точці цієї області.

Точки Z-площини, в яких однозначна функція f(z) аналітична, називають правильними точками цієї функції, а ті точки, в яких функція не є аналітичною, називають особливими точками.

Із властивостей диференційовних функцій випливає, що многочлен f(z) = a0 + a1z + a2z2 + ... + anzn ―

аналітична функція в усій комплексній площині.

Далі, якщо f(z) і φ(z) ― аналітичні функції в області D, то в цій області

будуть аналітичними також і функції сf(z), f(z) ± φ(z), f(z)·φ(z). Частка f (z)

ϕ(z)

(φ(z) ≠ 0) аналітична в області D*, утвореній з області D виключенням з неї тих точок z, в яких функція φ(z) обертається в нуль. Тобто дробово-

		a		+ a z + ... + a		zn
раціональна функція	f (z) =		0	1	n		є аналітичною функцією в
		b		+ b z + ... + b		zm

	0			1	m

області, яку дістаємо з усієї комплексної площини виключенням тих її точок, в яких знаменник дробу дорівнює нулю.

2.2. Гармонічні функції

Диференціальне рівняння з частинними похідними другого порядку

∂2 ϕ + ∂2 ϕ = 0 ∂x2 ∂y2

називають рівнянням Лапласа, а дійсну функцію φ(x, y), яка має в області D неперервні частинні похідні другого порядку включно і задовольняє це рівняння, називають гармонічною функцією в цій області.

Якщо функція f (z) = u(x, y) + iυ( x, y) аналітична в деякій області D, то дійсні функції u(x, y) та υ( x, y) задовольняють рівняння Лапласа, тоб-

то є гармонічними.

273

http://vk.com/studentu_tk, http://studentu.tk/

Гармонічні функції φ(x, y) і ψ (x, y) називають спряженими, якщо вони задовольняють умови Коші—Рімана:

	∂ϕ =	∂ψ ,	∂ϕ	= − ∂ψ .
	∂x	∂y	∂y	∂x
	Для тогощобфункція		f (z) = u(x, y) + iυ( x, y) булааналітич-
Теорема 2	Для тогощобфункція		f (z) = u(x, y) + iυ( x, y) булааналітич-
	ною в області D, необхідно і достатньо, щоб її дійсна части-
на u(x, y) і уявна частина υ( x, y)			були спряженими гармонічними функ-
ціями в цій області.

За даною гармонічною в однозв’язній області D функцією u(x, y) можна знайти нескінченну множину аналітичних у цій області функцій з дійсною частиною u(x, y). Уявну частину цих функцій визначають за формулою

(x, y)

∂v dx +

∂v dy =

(x, y)

∂u dx +

∂u dy =

υ ( x, y) = ∫

∫

−

( x ,

) ∂x

∂y

( x

, y )

∂y

∂x

∂u(x, y )

∂u(x, y)

dy + c.

= ∫ −

∂y

dx + ∫

∂x

Отже,

υ ( x,

−

∂u(x, y )

∂u(x, y)

dy + c,

(3.10)

y) = ∫

dx + ∫

∂x

∂y

де с ― довільна стала.

Аналогічно, нехай гармонічна функція υ( x, y) є уявною частиною ана-

літичної функції f(z) = u(x, y) + iυ(x, y), тоді її дійсну частину знаходять за формулою:

x	∂v(x, y )	y	∂v(x, y)
u(x, y) = ∫	0	dx + ∫ −		dy + c.	(3.11)
u(x, y) = ∫	∂y	dx + ∫ −	∂x	dy + c.	(3.11)
x0	∂y	y0	∂x
x0		y0

Зауваження. За точку (x0 , y0 ) можна взяти будь-яку фіксовану точ-

ку площини, в якій підінтегральні функції існують. Найзручнішою при цьому є точка (0; 0).

2.3. Геометричний зміст модуля й аргумента похідної

Нехай функція f (z) аналітична в точці z0 і f ′(z0 ) ≠ 0 . Проведемо через точку z0 гладку криву l.

274

http://vk.com/studentu_tk, http://studentu.tk/

Нехай функція f (z) відображає точку z0 площини Z

у точку w0 = f (z0 )

площини W , а криву l ― у криву L. Візьмемо в околі точки z0 на кривій l

довільну точку z0 + z і будемо наближати цю точку до точки z0 . Тоді то-

чка

w + w , яка відповідає точці z +

z ,

переміщуватиметься по кривій L

до точки w0 (рис. 3.4).

За означенням похідної

w .

f ′(z0 ) =

lim

z→0

Звідси випливають рівності

f ′(z0 )

lim

= lim

z→0

де

z − z0

― відстань між точками

z0 та z0 +

z ,

w − w0

―

відстань між точками w0 та w0 + w . Отже,

похідна

f ′(z0 )

є границею

відношення нескінченно малої відстані між точками w0

та w0 + w до не-

скінченно малої відстані між точками z0

та

z0 + z . Унаслідок аналітич-

ності функції f (z) ця границя не залежить від вибору кривої l , що прохо-

дить через точку z0 , тобто границя

lim

f ′(z0 )

у точці z0 стала й

однакова в будь-якому напрямку.

z→0

f ′(z0 )

Геометричний зміст модуля похідної: величина

дорівнює кое-

фіцієнту розтягу (подібності) в точці z0 при відображенні w = f (z) . Якщо

f ′(z0 )

> 1, то величину називають коефіцієнтом розтягу; якщо

f ′(z0 )

< 1 ,

то ― коефіцієнтом стиску.

Для аргументу похідної в точці z0 виконуються рівності:

arg f ′(z

) =

lim arg

w = lim arg

w − lim arg z = α

− α ,

z→0

де α1 таα2 ― кути, які утворюють дотичні до кривих l і L	у точках z0 та
w0 відповідно з додатними напрямами дійсних осей площин	Z і W.

Звідси α2 = α1 + arg f ′(z0 ) . Отже, аргумент похідної f ′(z0 )	геомет-
рично дорівнює куту, на який треба повернути дотичну в точці z0	до будь-
якої гладкої кривої на площині Z , що проходить через точку z0 ,	щоб діс-

тати напрямок дотичної в точці w0 = f (z0 ) до образу цієї кривої на площині W при відображенні w = f (z) .

275

http://vk.com/studentu_tk, http://studentu.tk/

y				v	w = w0 + w
l		z = z0	+ z		w
	z	z = z0	+ z		L
z0	z				w0
z0					w0
α1			x		α2
			x		u

Рис. 3.4

2.4. Інтегрування функції комплексної змінної

Нехай однозначна функція f (z) визначена і неперервна в області D, а

L ― кусково-гладка крива, яка належить D.

Нехай z = x + iy , f (z) = u + iv , u = u(x, y) , v = v(x, y) .

Інтеграл від функції f(z) уздовж кривої L визначається так:

∫ f (z)dz = ∫(u + iv)(dx + idy) = ∫udx − vdy + i∫ vdx + udy.				(3.12)
L	L	L	L

Отже, інтеграл за комплексною змінною є сумою двох криволінійних інтегралів другого роду від функцій двох дійсних змінних.

Якщо функції u і υ неперервні вздовж гладкої дуги, заданої параметри-

чно: x = x(t) , y = y(t) ,	t [α; β] , то
	β
∫ udx − vdy = ∫[u(x(t), y(t))x′(t) − v(x(t), y(t)) y′(t)]dt,
L	α
	β
∫ vdx + udy = ∫[v(x(t), y(t))x′(t) + u(x(t), y(t)) y′(t)]dt.
L	α
Враховуючи, що
u(x(t), y(t)) + i v(x(t), y(t)) = f(z(t)) і z′(t) = x′(t) + iy′(t) ,
можна записати:
	β	β
∫ f (z)dz = ∫ (u + iv)(x′ + iy′)dt = ∫ f (z(t))z′(t)dt.			(3.13)
L	α	α

Формула (3.13) зводить обчислення інтеграла за комплексною змінною від функції f(z) до обчислення визначеного інтеграла на відрізку [α; β] від дійсної змінної t.

276

http://vk.com/studentu_tk, http://studentu.tk/

Теорема 3

Інтеграл ∫ f (z)dz існує для будь-якої неперервної функції f(z) і будь-

якої гладкої кривої L.

(інтегральна теорема Коші). Якщо функція f(z) аналітична в однозв’язній області D і L ― кусково-гладкий замкнений

контур, що цілком міститься в D, то

v∫ f (z)dz = 0.	(3.14)
L

Інтегральна теорема Коші справджується й у разі, коли область D є багатозв’язною (див. рис. 2.44).

Теорема 4 Нехай багатозв’язнаобластьD обмежена зовнішнім контуром L, орієнтованим проти ходу годинникової стрілки, і внутрішніми контурами L1, L2, …, LN, орієнтованими теж проти ходу годиннико-

вої стрілки, і нехай в D задана аналітична функція f(z). Тоді

v∫	N
v∫	f (z)dz = ∑ v∫ f (z)dz .	(3.15)
L	k =1 Lk

Інтеграли від функції f(z), аналітичної в однозв’язній області D, не залежать від форми шляху інтегрування, а залежать лише від початкової і кінцевої точок. Тому для інтеграла вздовж кривої L, що сполучає точки z0 і z, користуються позначенням

z∫0 f (ς)dς .

Теорема 5 Нехай f(z) ― функція, неперервна в однозв’язній області D, й інтеграл від цієї функції вздовж довільної кусково-гладкої кривої, яка цілком лежить у D, не залежить від форми цієї кривої. Тоді фу-

нкція

z
F(z) = ∫ f (ς)dς ,
z0
′	′
де z0 , z D , має похідну F (z) , причому	F (z) = f (z) .

Функцію F(z) називають первісною для f (z), якщо F ′(z) = f (z) для всіх

z D.

Якщо F(z) ― первісна для f (z), то Ф(z) = F(z) + c, де с — комплексна стала, також первісна для f (z).

Теорема 6 Якщо f (z) ― аналітична функція в однозв’язній облaсті D і Ф(z) ― будь-яка первісна для f (z), то

277

http://vk.com/studentu_tk, http://studentu.tk/

z2	f (z)dz = Φ(z2 ) − Φ(z1 ) ,	(3.16)
∫	f (z)dz = Φ(z2 ) − Φ(z1 ) ,	(3.16)
z1

де z1, z2 D й інтегрування відбувається вздовж будь-якої кусково-гладкої дуги, що цілком лежить у D і сполучає точки z1 і z2.

Формулу (3.16) називають формулою Ньютона—Лейбніца.

Інтеграли від елементарних функцій комплексної змінної в області аналітичності обчислюють за допомогою тих самих правил і формул, що й від функцій дійсної змінної.

2.5. Інтегральна формула Коші

Теорема 7 Нехай функція f (z) аналітична в однозв’язній замкненій об-

ласті D , L ― межа області D, орієнтована в додатному напрямку (тобто проти ходу годинникової стрілки). Тоді для будь-якої внутрішньої точки z0 D справджується інтегральна формула Коші:

f (z0 ) =

v∫

f (z)dz

(3.17)

2πi

z − z

Якщо z0 не належить

, то

f (z)dz

= 0 .

2πi v∫

z − z

v∫

f (z)dz

називають інтегралом Коші.

Вираз

2πi

z − z

ФормулаКошімаємісцеідлябагатозв’язноїобласті.

Важливість формули (3.17) полягає в тому, що

вона виражає

значення

аналітичної функції

f (z) в

Рис. 3.5

довільній внутрішній точці області D через її значен-

ня на межі цієї області.

Теорема 8 Нехай f(z) ― аналітична в області D функція і L ― кусковогладкий додатно орієнтовний замкнений контур, який ціл-

ком лежить у D разом з усіма своїми внутрішніми точками. Тоді для точок z0, які лежать усередині L, виконуються рівності

f (n) (z0 ) =	n!		f (ς)dς	( n = 0, 1, 2,... ).	(3.18)
	2πi	v∫L (ς − z0 )n+1

Формули (3.17) та (3.18) — конструктивний засіб для обчислення інтегралів. За умов теорем 7 та 8 виконуються рівності

	f (ς)dς	= 2πif (z0 ),		f (ς)dς	=	2πi	f (n) (z0 ).
v∫L (ς − z0 )			v∫L (ς − z0 )n+1			n!

278

http://vk.com/studentu_tk, http://studentu.tk/

Т.2 ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ

1. Перевірте, чи диференційовна функція f (z) = z .

Розв’язання. Очевидно, що розглядувана функція неперервна на всій комплексній площині.

Для заданої функції при будь-якому z дістаємо

f (z) =

z + z

− z

x − i y

x + i y

Із цієї рівності випливає:

f (z)

1) якщо ∆y = 0, ∆x ≠ 0, то

= 1;

2) якщо ∆x = 0, ∆y ≠ 0, то

f (z)

= –1.

x − i

Отже, вираз

при ∆z → 0 границі не має при жодному z.

x + i

Таким чином, функція f (z) = z , що неперервна в усій комплексній площині, не має похідної в жодній точці площини, тобто не є диференційовною.

2. Дослідітьнадиференційовністьфункціюf (z) = z2 тазнайдіть їїпохідну.

Розв’язання. Нехай z = x + iy, тоді

z2 = (x + iy)2 = x2 – y2 + 2ixy, u(x, y) = x2 – y2, υ(x, y) = 2xy.

Дійсні функції u(x, y) i υ(x, y) диференційовні в будь-якій точці (x, y) і задовольняють умови Коші—Рімана:

∂u	=	∂v	= 2x ,	∂u	= −	∂v	= −2 y .
∂x		∂y		∂y		∂x

Звідси випливає, що функція f (z) = z2 диференційовна на всій комплексній площині. Використовуючи формулу (3.9), маємо

(z2 )′ = 2x + 2iy = 2(x + iy) = 2z.

3. Дослідіть аналітичність функцій: а) f (z) = z z ; б) f (z) = e2z.

Розв’язання: а) маємо z z = x2 + y2, отже, u(x, y) = x2 + y2, υ(x, y) = 0.

Умови Коші―Рімана мають вигляд:

2x = 0,

2y = 0

і виконуються лише в точці (0; 0).

279

http://vk.com/studentu_tk, http://studentu.tk/

Отже, функція f (z) = z z диференційовна тільки в точці z = 0 і ніде не аналітична.

Обчислимо похідну f ′(0) , користуючись означенням. Враховуючи, що f(0) = 0, дістанемо

lim

z→0

Отже, похідна

∆f = f(0 + ∆z) – f(0) = ∆z z ,

f	= lim	z	z	= lim	z = lim ( x − i y) = 0.
z	= lim	z		= lim	z = lim ( x − i y) = 0.
z	z→0	z		z→0	x→0
					y→0

f ′(0) існує й дорівнює нулю;

б) маємо e2z = e2x(cos 2y + isin 2y), звідси u(x, y) = e2xcos 2y, υ (x, y) = = e2xsin 2y — диференційовні функції у будь-якій точці (х, у). Знайдемо частинні похідні

∂u		= 2e2 x cos 2 y,	∂u		= −2e2 x sin 2 y,

∂x			∂y
	∂v	= 2e2 x sin 2 y,		∂v	= 2e2 x cos 2 y.

	∂x			∂y

Оскільки умови Коші―Рімана виконуються на всій площині, то задана функція диференційовна для будь-якого z і її похідна має вигляд:

(e2z )′ =	∂u	+ i	∂v	= 2e2xcos 2y + i2e2xsin 2y = 2e2x(cos 2y + isin 2y) = 2e2z.
	∂x		∂x

4. Чи будуть диференційовними функції:

а) f (z) = y + xi; б) f (z) = (x2 – y2) + 2xyi; в) f (z) = excos y + iexsin y?

Розв’язання: а) u = y, υ = x;	∂u	= 0,	∂u	= 1,	∂v	= 1,	∂v	= 0.

	∂x		∂y		∂x		∂y

Одна з умов Коші―Рімана не виконується: ∂u ≠ ∂v . Тому розглядува-

∂y ∂x

на функція недиференційовна;

б) u = x2 – y2, υ = 2xy;

∂u

= 2x,

∂u

= −2 y,

∂v

= 2 y,

∂v

= 2x;

∂u

∂v

= −

∂u

∂x

∂y

∂x

∂y

∂x

∂y

∂x

∂y

Умови Коші―Рімана виконуються. Отже, за теоремою 1 функція диференційовна. Похідну знаходимо за формулою (3.9):

280

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 16 17 18 19 20 21 22 23 24 25 26 2728 / 4528 29 30 31 32 33 34 35 36 37 38 39 40 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2019882.69 Кб36Vikova_psikhol_Konsp_Alp.doc
#
19.02.2016908.69 Кб55Vischa_geodeziya.docx
#
19.02.20168.29 Mб315Vischa_matematika_Chastina_1_Denisyuk_Repeta.pdf
#
19.02.20164.86 Mб918Vischa_matematika_Chastina_2_Denisyuk_Repeta.pdf
#
19.02.20162.32 Mб223Vischa_matematika_Chastina_2_Denisyuk_Repeta.pdf
#
19.02.20167.52 Mб414Vischa_matematika_Chastina_3_Denisyuk_Repeta.pdf
#
19.02.20161.68 Mб74Vitorskaya_N_Prichiny_Bolezn_Istoki_Zdorov_Pra.doc
#
26.08.201978.26 Кб0voprosy_1-10.docx
#
19.02.201650.69 Кб79Voprosy_na_ekzamen_TS.doc
#
19.02.20161.5 Mб8vsesvitny_istoria_shupak1-39.pdf
#
09.12.2018260.17 Кб18vse_gotovo.docx