Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Vischa_matematika_Chastina_3_Denisyuk_Repeta

.pdf

Скачиваний:

414

Добавлен:

19.02.2016

Размер:

7.52 Mб

Скачать

☆

<<< < Предыдущая 21 22 23 24 25 26 27 28 29 30 31 32 33 3435 / 4535 36 37 38 39 40 41 42 43 44 45 > Следующая >>>

2. Нехай f (0) = f ′(0) = ... = f (n) (0) , тоді f(t) F(p),

f ′(t)	pF(p),
f ′′(t)	p2 F( p) ,

..........................

f (n) (t) pn F( p) . 70. Диференціювання зображення.

Нехай f(t) F(p), Re p > σ0 , тоді

–t f(t)	dF( p)	.

	dp

Застосовуючи операцію диференціювання багаторазово, дістають формулу

		(−t)n f (t)			d n F( p)		,
або		(−t)n f (t)				dpn	,
						dpn


	t	n	f (t)	(−1)	n d n F( p)			.
	t		f (t)	(−1)		dpn		.
						dpn

Зауваження. Зазначимо, що коли f(t) ― оригінал, то tn f (t) ― також оригінал.

80. Інтегрування оригіналу.

Нехай f(t)	F(p), тоді
		t		1
		∫ f (τ)d τ		1		F( p) .
		∫ f (τ)d τ			p	F( p) .
		0			p
		0

90. Інтегрування зображення.

Нехай f(t)	F (p) і	f (t)	― оригінал, тоді
Нехай f(t)	F (p) і	t	― оригінал, тоді
		t		∞
			f (t)	∞
			f (t)	∫ F( p)dp.
			t	∫ F( p)dp.
			t	p
				p

						341

http://vk.com/studentu_tk, http://studentu.tk/

100. Згортка оригіналів (теорема множення).

Згорткою неперервних функцій f (t) і φ(t) називають функціюψ(t) , що визначається формулою

t	t
ψ(t) = f (t) ϕ(t) = ∫ f (τ)ϕ(t − τ)d τ = ∫ f (t − τ)ϕ(τ)d τ.
0	0
Нехай f1(t) F1(p) і f2(t) F2(p), тоді
f1 (t) f2 (t)	F1(p) · F2(p),

тобто згортці оригіналів відповідає добуток зображень оригіналів.

110. (граничні співвідношення). Нехайf(t)			F(p ) і f ′(t) ― оригінал, тоді
1) lim	pF( p) = lim f (t) ;
p→∞	t→+0
2) якщо існує границя lim		f (t) , то lim pF( p) = lim f (t) .
	t→+∞	p→0	t→+∞
	1.5. Зображення періодичних і ступінчастих функцій

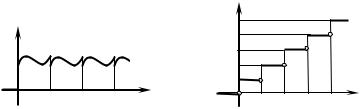
	Теорема	Нехай	f (t) ― функція-оригінал з періодом Т (рис. 4.3), тобто
		f (t) = f (t + T ) = f (t + 2T ) = ... , t ≥ 0 .
	Тоді						T
					1		T
			f (t)		1		∫ f (t)e− pt dt.		(4.5)
			f (t)		− e	− pT	∫ f (t)e− pt dt.		(4.5)
				1	− e		0
	Доведення. Нехай		f (t)	F(p). Оскільки				f (t) = f (t + T), то f (t + T)	F(p).
За формулою (4.4)
		f(t + Т)					T
		f(t + Т)		epТ F( p) − ∫ e− pt f (t)dt .
							0

Отже,

	T
F( p) = epТ F( p) − ∫ e− pt f (t)dt .
	0

Розв’язавши це рівняння відносно F( p) , дістанемо

	1		T
F( p) =			∫ f (t)e− pt dt ,
	− e	− pT
1			0

342

http://vk.com/studentu_tk, http://studentu.tk/

що доводить твердження теореми.

			f(t)
f(t)			4A
			3A
			2A
			A
О	Т 2Т 3Т	t	О	τ 2τ 3τ 4τ t
	Рис. 4.3			Рис. 4.4

У прикладних задачах часто доводиться зустрічатися з так званими ступінчастими функціями (рис. 4.4), які характеризуються наявністю різних аналітичних виразів на різних проміжках значень аргументу. Вони є кусково-сталими функціями, тому їх можна будувати за допомогою функцій Хевісайда й отримувати зображення згідно з властивістю запізнення оригіналу.

Наприклад, нескінченну ступінчасту функцію f (t) , зображену на рис.4.4, за допомогою функцій Хевісайда можна подати у вигляді

f (t) = A(η(t) − η(t − τ)) + 2A(η(t − τ) − η(t − 2τ)) +

+3A(η(t − 2τ) − η(t − 3τ)) + ... = A(η(t) + η(t − τ) + η(t − 2τ) + ...) .

За властивістю 40 функції Хевісайда η(t − t

) , де t

> 0 , відповідає зо-

браження

e−t0 p , тоді

− pτ

−2 pτ

− pτ

−2 pτ

L(f (t))=A

+ ...

(1+ e

+ e

+ ...) .

Обчислившисумунескінченно спадноїгеометричної прогресії, дістанемо

L(f (t))=	A	1	.
	p	1− e− pτ

Аналогічно знаходять зображення будь-яких кусково-неперервних функцій. При цьому у загальному випадку функцію

f1 (t)			для	t [0;	a1 ),
	2 (t)		для	t [a1 ; a2 ),
f	2 (t)		для	t [a1 ; a2 ),
								(4.6)
f (t) = .......................................								(4.6)
f	k	(t)	для	t [a	−1	;	a	),
	k	0	для	k	−1		k
		0	для	t < 0 або t ≥ a .
								k
								343

http://vk.com/studentu_tk, http://studentu.tk/

записують у вигляді

f (t) = f1 (t)(η(t) − η(t − a1 )) + f2 (t)(η(t − a1 ) − η(t − a2 )) +						(4.7)
		+ …+ fk (t)(η(t − ak −1 ) − η(t − ak )) .				(4.7)
		+ …+ fk (t)(η(t − ak −1 ) − η(t − ak )) .

	Т.1	ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
1. Покажіть, що функція
			2t	sin 3t	для t ≥ 0,
		f (t) = e		sin 3t	для t ≥ 0,
				0	для t < 0

є функцією-оригіналом.

Розв’язання. Справді, функція f (t) задовольняє умови:

1)f (t) неперервна на всій осі t;

2)f(t) = 0 для t < 0;

3)для всіх t > 0 виконується нерівність

e2t

sin 3t

≤ e2t , σ0

= 2 .

Отже, f (t) ― функція-оригінал.

2. Покажіть, що

sin t

, та cos t

p2 + 1

p2 +

Розв’язання. Використовуючи формули Ейлера

дістанемо

eit

= cos t + i sin t ,

e−it

= cos t − i sin t ,

eit − e−it

eit

+ e−it

sin t =

cos t =

За властивістю лінійності

L(sin t) =

L(eit

) −

L(e−it )

−

2i p − i

2i p + i

p + i − ( p − i)

p2 + 1

Аналогічно дістаємо зображення для cos t :

L(cos t) =

L(e

) +

L(e

−it

) =

p − i

p + i

+ 1

344

http://vk.com/studentu_tk, http://studentu.tk/

3. Знайдіть зображення функцій eαt , sin ωt, cos ωt , користуючись вла-

стивістю 30 (подібності). Розв’язання. Маємо

L(eαt ) =

;

p − α

− α

− 1

L(sin ωt) =

ω2

;

p 2

p2 + ω2

+ 1

ω2

L(cos ωt) =

p 2

+ ω2

p2 + ω2

+ 1

Отже,

eαt

sin ωt

cos ωt

p − α

2 + ω2

p2 + ω2

4. Знайдіть зображення одиничної функції Хевісайда «із запізненням»:

для t

≥ τ,

(рис. 4.5)

f(t)

η(t − τ) =

для t

< τ.

f(t) = η(t– τ)

Розв’язання. Використовуючи властивість 40 (за-

пізнення оригіналу), дістанемо

e− pτ

–pτ

η(t − τ)

·L(η(t)) =

Рис. 4.5

5. Знайдіть зображення функцій sin (ωt – φ) i cos (ωt – φ). Розв’язання. Використовуючи властивості 30 та 40, дістанемо

sin (ωt − ϕ) = sinω (t −	ϕ	)	1
			ω
	ω

−

ω ,

p 2

+ ω2

+ 1

345

http://vk.com/studentu_tk, http://studentu.tk/

cos (ωt − ϕ) = cosω (t −	ϕ	)	1
			ω
	ω

−

+ 1

+ ω

6. Знайдіть зображення функції f (t) = e−tcos 2t.

Розв’язання. Враховуючи, що cos 2t

, за властивістю 50 (змі-

щення зображення) (p0 = –1) маємо

p2 + 4

e−tcos 2t

p + 1

( p + 1)2 + 4

p2 + 2 p + 5

7. Знайдіть зображення функції f (t) = sin2 t.

Розв’язання. Перший спосіб. Запишемо f (t) у вигляді

(t) =

(1− cos 2t) .

Використовуючи властивості 20 та 30, дістанемо

f (t) =

(1− cos 2t)

−

+ 4

p( p

+ 4)

Другий спосіб. Нехай f (t) F (p). Тоді за властивістю 60 (диференцію-

вання оригіналу)

f ′(t) pF(p) – f(0). Але f (0) = sin2 0 = 0, отже,

′

(t) = (sin

′

= 2sin t cos t = sin 2t

p2 + 4 .

Звідси випливає, що

= pF ( p).

2 +

Отже, F( p) =

sin2 t.

p( p2 + 4)

8. Знайдіть зображення функції f (t) = tn.

Розв’язання. Відомо, що η (t )

. Тоді, використовуючи властивість

70 (диференціювання зображення), послідовно дістанемо

346

http://vk.com/studentu_tk, http://studentu.tk/

−t η(t)

1 ′

−1

або

;

η(t)

−1

′

. . . . . . . . . . . . . . . . . . . . . .,

tn η(t)

pn+1

9. Знайдіть зображення функції f (t) = t2et.

Розв’язання. Відомо, що et 1 . За властивістю 70 (диференціювання p − 1

зображення) маємо

	1		′			t			1						t
					– t e , тобто								t e .
					– t e , тобто			( p −		1)	2		t e .
p −		1						( p −		1)
Використовуючи цю властивість ще раз, дістаємо
	1				′	2 t	2		t		2
					t e , звідки t				e							.
		1)		2	t e , звідки t				e			( p −		1)	3	.
( p −		1)										( p −		1)
								t
10. Знайдіть зображення функції							f (t) = ∫ eτ d τ.
							0

Розв’язання. Використовуючи властивість 80 (інтегрування оригіналу) і

враховуючи, що et

, дістанемо

− 1

f (t) = ∫ eτ d τ

p − 1

p( p − 1)

11. Знайдіть зображення функції

f (t) =

sin t

Розв’язання. Враховуючи, що sin t

, і скориставшись власти-

p2 + 1

вістю 90 (інтегрування зображення), дістанемо

347

http://vk.com/studentu_tk, http://studentu.tk/

sin t	+∞	dp			a		π	− arctg p = arcctg p.
	∫		= lim arctg	p		=
t		p2 + 1			p
	p		a→∞			2

12. Знайдіть згортку функцій t і cos t та її зображення.

Розв’язання. Нехай f (t) = t, ϕ(t) = cos t. Тоді

f (t) ϕ(t) = ∫ τ cos (t − τ)d τ.

Для обчисленняінтегралавикористаємо методінтегруваннячастинами.

∫

+∫ sin(t

	u = τ du = d τ				t +
	u = τ du = d τ
τ cos(t − τ)d τ =	cos(t − τ)d τ = dv	= −τ sin(t − τ)
τ cos(t − τ)d τ =	cos(t − τ)d τ = dv	= −τ sin(t − τ)
	v = −sin(t − τ)				0
					0

− τ)d τ = −t sin(t − t) + 0 sin(t − 0) + cos(t − τ)			t	= 1− cos t.
− τ)d τ = −t sin(t − t) + 0 sin(t − 0) + cos(t − τ)			t	= 1− cos t.
			0
			0

Отже,

t cos t = 1− cos t.

Зображення F(p) цієї згортки за властивістю 100 має вигляд

F( p) = L(t) L(cos t) =		1	p	=	1		.
F( p) = L(t) L(cos t) =		p2	p2 + 1	=	p( p2	+ 1)	.
		p2	p2 + 1		p( p2	+ 1)
13. Знайдіть зображення ступінчастої функції
2	для	0 ≤ t < 1,
	для	1 ≤ t < 2,
3	для	1 ≤ t < 2,
f (t) =	для	3 ≤ t < 6,
1	для	3 ≤ t < 6,
0	для	t < 0 або t ≥ 6.

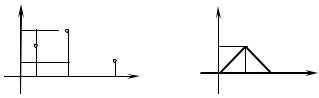
Розв’язання. Графік заданої функції зображено на рис. 4.6. Використовуючи функції Хевісайда η(t), η(t − 1), η(t − 3), η(t − 6) , запишемо f (t) одним аналітичним виразом. Маємо

f (t) = 2(η(t) − η(t − 1)) + 3(η(t − 1) − η(t − 3)) + η(t − 3) − η(t − 6) .

Тут вираз 2(η(t) − η(t −1)) визначає графік функції f (t) на проміжку

(0; 1) , 3(η(t − 1) − η(t − 3)) ― на проміжку (1; 3) , а η(t − 3) − η(t − 6) ― на проміжку (3; 6) .

348

http://vk.com/studentu_tk, http://studentu.tk/

Враховуючи, що η(t)

, і скориставшись властивістю 40 (запізнен-

ня оригіналу), дістанемо

f (t)

e− p

e−3 p

e−6 p

−

e− p

−

2e−3 p

−

e−6 p

(2 + e− p

− 2e−3 p − e−6 p ).

f(t)

Рис. 4.6

Рис. 4.7

14. Знайдіть зображення функції, заданої графіком (рис. 4.7).

Розв’язання. Знайдемо аналітичний вираз для f (t):

для

0 ≤ t ≤ 1,

2 − t

для

1 < t < 2,

f (t) =

для

t < 0 або t ≥ 2.

Використовуючи функції Хевісайда, подамо f (t) у вигляді:

f(t) = t(η(t) − η(t − 1)) + (−t + 2)(η(t − 1) − η(t − 2)) =

=tη(t) − tη(t − 1) − (t − 2)η(t − 1) + (t − 2)η(t − 2) =

=tη(t) − 2(t − 1)η(t − 1) + (t − 2)η(t − 2) .

За властивістю 40 (запізнення оригіналу) дістанемо

f(t)	1	−	2e− p	+	e−2 p	=	1	(1 − 2e− p + e−2 p ) =		(1 − e− p )2	.
	p2		p2		p2		p2			p2
15. Знайдіть зображення функції
								для t	< 1,
						0		для t	< 1,
						2		для 1 ≤ t ≤ 2,
				f (t) = t				для 1 ≤ t ≤ 2,
						0		для t	> 2.

349

http://vk.com/studentu_tk, http://studentu.tk/

Розв’язання. Запишемо f (t) у вигляді

f (t) = t2 (η(t − 1) − η(t − 2)) = t2 η(t − 1) − t2 η(t − 2).

Виразимо f (t) через різниці (t – 1) та (t – 2). Маємо

t2 = ((t − 1) + 1)2 = (t − 1)2 + 2(t − 1) + 1, t2 = ((t − 2) + 2)2 = (t − 2)2 + 4(t − 2) + 4.

Тоді

f (t) = ((t − 1)2 + 2(t − 1) + 1)η(t − 1) − ((t − 2)2 + 4(t − 2) + 4)η(t − 2) .

Оскільки η (t )

tη(t)

η(t)

, то за властивістю 40

(запізнення оригіналу), дістанемо

− p

−2 p

L( f (t)) =

−

16. Знайдіть зображення F (p) функції f (t), заданої графіком (рис. 4.8). Розв’язання. Склавши рівняння відповідних відрізків, запишемо аналі-

тичний вираз функції f (t):

äëÿ

t (0; a),

äëÿ

t (a; 2a),

t −

äëÿ

t (2a;3a),

f (t) =

− 3a)

1−

äëÿ t (3a; 4a),

äëÿ

t < 0 àáî t > 4a,

тобто функцію вигляду (4.6). За формулою (4.7) маємо

f (t) = 1 (η(t) − η(t − a)) +

t − 2a

(η(t − 2a) − η(t − 3a)) +

+ 1

−

t − 3a

(η(t − 3a) − η(t −

4a)) = η(t) − η(t − a) +

t − 2a

η(t

− 2a) +

350

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 21 22 23 24 25 26 27 28 29 30 31 32 33 3435 / 4535 36 37 38 39 40 41 42 43 44 45 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2019882.69 Кб33Vikova_psikhol_Konsp_Alp.doc
#
19.02.2016908.69 Кб55Vischa_geodeziya.docx
#
19.02.20168.29 Mб315Vischa_matematika_Chastina_1_Denisyuk_Repeta.pdf
#
19.02.20164.86 Mб918Vischa_matematika_Chastina_2_Denisyuk_Repeta.pdf
#
19.02.20162.32 Mб223Vischa_matematika_Chastina_2_Denisyuk_Repeta.pdf
#
19.02.20167.52 Mб414Vischa_matematika_Chastina_3_Denisyuk_Repeta.pdf
#
19.02.20161.68 Mб74Vitorskaya_N_Prichiny_Bolezn_Istoki_Zdorov_Pra.doc
#
26.08.201978.26 Кб0voprosy_1-10.docx
#
19.02.201650.69 Кб79Voprosy_na_ekzamen_TS.doc
#
19.02.20161.5 Mб8vsesvitny_istoria_shupak1-39.pdf
#
09.12.2018260.17 Кб18vse_gotovo.docx