
- •Глава I. Линейная алгебра
- •§1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства определителей
- •§2. Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца
- •§3. Операции над матрицами
- •§4. Системы линейных алгебраических уравнений (слау). Матричный метод решения
- •§5. Метод Гаусса для исследования и решения слау
- •§6. Однородные системы линейных алгебраических уравнений
- •Глава 2. Элементы векторной алгебры и аналитической геометрии
- •§1. Векторы и линейные операции над ними
- •§2. Базис векторного пространства. Координаты вектора
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§3. Скалярное произведение векторов и его свойства
- •§4. Векторное произведение векторов и его свойства
- •§5. Смешанное произведение векторов
- •§6. Прямая на плоскости
- •§7. Плоскость в пространстве
- •§8. Прямая в пространстве
- •§9. Кривые второго порядка на плоскости
- •§10. Основные понятия об n-мерном арифметическом пространстве
- •Глава 3. Введение в анализ.
- •§1. Функции
- •1.1. Функция. Способы задания функций
- •1.2. Элементарные функции
- •§2. Теория пределов
- •2.1. Последовательность и её предел
- •2.2. Предел функции
- •§3. Бесконечно малые и бесконечно большие функции
- •3.5. Сравнение бесконечно малых
- •§4. Непрерывность функций. Точки разрыва
- •4.1. Непрерывность функции в точке
- •4.2. Классификация точек разрыва
- •Глава 4. Дифференциальное исчисление фуннкций одной переменной
- •§1. Приращения и производные
- •§2. Механический и геометрический смыслы производной
- •§3. Правила дифференцирования
- •§4. Дифференциал функции
- •§5. Производные и дифференциалы высших порядков
- •§6. Правило Лопиталя. Раскрытие неопределенностей
- •§7. Исследование функций с помощью производных
- •7.1. Монотонность и экстремумы функции
- •7.2. Выпуклость и точки перегиба функции
- •7.3. Асимптоты графика функции.
- •7.4. Схема исследования и построения графика функции
- •6. Построение таблицы, в которой указываются все найденные точки разрыва, критические точки первого и второго порядка и интервалы между ними. В каждом интервале характеризуется поведение функции.
- •Глава 5. Функции нескольких переменных
- •§1. Основные понятия о функциях нескольких переменных
- •1.2. Способы задания функции нескольких переменных
- •§2. Дифференцирование функций нескольких переменных
- •2.1. Частные приращения и частные производные
- •2.2. Полное приращение и полный дифференциал
- •§3. Производные и дифференциалы высших порядков
- •§4. Экстремумы функции нескольких переменных
- •Глава 6. Неопределенные и определенные интегралы
- •§1. Первообразная и неопределенный интеграл. Их свойства
- •1.1. Основные определения
- •1.2. Таблица основных неопределенных интегралов
- •§3. Определенный интеграл как предел интегральных сумм
- •§4. Свойства определенного интеграла
- •§5. Несобственные интегралы
- •Глава 7. Обыкновенные дифференциальные уравнения
- •§1. Основные понятия об уравнениях первого порядка
- •§2. Уравнения с разделяющимися переменными
- •§3. Однородные уравнения первого порядка
- •§4. Линейные уравнения первого порядка
- •§5. Основные понятия об уравнениях высшего порядка
- •§6. Линейные дифференциальные уравнения (лду)
- •6.1. Линейные дифференциальные уравнения n-го порядка
- •6.2. Однородные линейные дифференциальные уравнения (олду)
- •6.3. Линейная независимость функций
- •6.4. Общее решение линейного однородного дифференциального уравнения n-го порядка
- •6.5. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •6.6. Общее решение линейного неоднородного дифференциального уравнения
- •6.7. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специального вида правой частью.
- •Содержание
Глава 4. Дифференциальное исчисление фуннкций одной переменной
§1. Приращения и производные
Пусть функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() .
.
Приращением
аргумента
х в точке
![]() называется разность
называется разность
![]() .
.
П риращением
функции
риращением
функции
![]() в точке
в точке![]() называется разность
называется разность
![]() .
.
Геометрически х
и f
означают изменения абсциссы и ординаты
точки на графике
![]() при перемещении из точки
при перемещении из точки![]() в точку
в точку![]() (рис. 1).
(рис. 1).
Следующее определение
непрерывности функции в точке
![]() эквивалентно предыдущему.
эквивалентно предыдущему.
Определение.
Если функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() и
и![]() ,
то она называетсянепрерывной
в точке
,
то она называетсянепрерывной
в точке
![]() .
.
Определение. Если существует предел
![]() , (1)
, (1)
то это число
называется производной
функции
![]() в точке
в точке![]() .
.
Эта производная обозначается также одним из следующих символов:
![]() .
.
Если функция
![]() имеет конечную производную в точке
имеет конечную производную в точке![]() ,
то она называетсядифференцируемой
в этой точке
(т. е. предел (1) существует).
,
то она называетсядифференцируемой
в этой точке
(т. е. предел (1) существует).
Теорема.
Если функция
![]() дифференцируема в точке
дифференцируема в точке![]() ,
то она непрерывна в этой точке.
,
то она непрерывна в этой точке.
§2. Механический и геометрический смыслы производной
2.1.
Пусть некоторая точка движется вдоль
прямой и за время t
проходит путь S(t).
Тогда за
промежуток времени от
![]() до
до![]() она проходит путь
она проходит путь![]() ,
и средняя скорость точки на промежутке
,
и средняя скорость точки на промежутке![]() равна
равна![]() .
Мгновенная скоростьv
точки в
момент
.
Мгновенная скоростьv
точки в
момент
![]() равна пределу
равна пределу![]() при
при![]() :
:
![]() .
Итак, мгновенная скорость точки в момент
.
Итак, мгновенная скорость точки в момент![]() равна
производной от пути, проходимого этой
точкой по времени
при
равна
производной от пути, проходимого этой
точкой по времени
при
![]() .
Это и естьмеханический
смысл производной.
.
Это и естьмеханический
смысл производной.
2.2.
Проведём прямую через две точки
![]() и
и![]() ,
лежащие на графике функции
,
лежащие на графике функции![]() .
Эта прямая называетсясекущей
к графику
функции (рис. 2). Её угловой коэффициент,
т. е. тангенс угла наклона к оси Оx
равен
.
Эта прямая называетсясекущей
к графику
функции (рис. 2). Её угловой коэффициент,
т. е. тангенс угла наклона к оси Оx
равен
![]() . (2)
. (2)
О пределение.
Касательной
к графику функции
пределение.
Касательной
к графику функции
![]() в точке
в точке![]() называется прямая, являющаяся предельным
положением секущей, проходящей через
точкуA
называется прямая, являющаяся предельным
положением секущей, проходящей через
точкуA![]() при
при![]() .
.
Касательная
![]() в точке
в точке![]() - это прямая, проходящая через
- это прямая, проходящая через![]() ,
угловой коэффициент которой равен
,
угловой коэффициент которой равен![]() .
.
Таким образом,
![]() есть угловой коэффициент касательной
к графику
есть угловой коэффициент касательной
к графику![]() в точке
в точке![]() (геометрический
смысл производной).
(геометрический
смысл производной).
Уравнение
этой касательной
имеет вид:
![]()
§3. Правила дифференцирования
Теорема 1.
(правила
дифференцирования суммы, произведения
и частного).
Если
функции
![]() и
и![]() дифференцируемы в точке х, то сумма,
произведение и частное этих функций
(частное при условии, что
дифференцируемы в точке х, то сумма,
произведение и частное этих функций
(частное при условии, что![]() )
также дифференцируемы в этой точке и
имеют место следующие формулы:
)
также дифференцируемы в этой точке и
имеют место следующие формулы:
1.
![]() 2.
2.![]() 3.
3.![]() .
(3).
.
(3).
Теорема 2.
(правило
дифференцирования сложной функции).
Пусть
функция
![]() дифференцируема в точке
дифференцируема в точке![]() ,
,![]() ,
функция
,
функция![]() дифференцируема в точке
дифференцируема в точке![]() ,
тогда сложная функция
,
тогда сложная функция![]() дифференцируема в
дифференцируема в![]() и её производная равна
и её производная равна
![]() .
.
Таблица производных основных элементарных функций.
Здесь
с,
а – постоянные,
а>0,
![]()


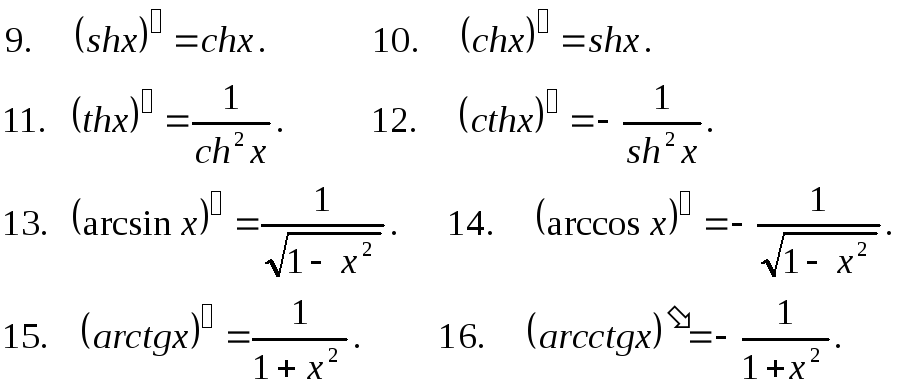
§4. Дифференциал функции
Определение.
Если приращение
функции
![]() в точке
в точке![]() можно представить в виде
можно представить в виде![]() ,
гдеa
- число,
а
,
гдеa
- число,
а
![]() -
б.м. при
-
б.м. при![]() ,
то величина
,
то величина![]() называется
дифференциалом
функции
называется
дифференциалом
функции
![]() в точке
в точке![]() (главной частью приращения).
(главной частью приращения).
Т еорема
о
дифференциале.
Для того
чтобы функция
еорема
о
дифференциале.
Для того
чтобы функция
![]() имела дифференциал в точке
имела дифференциал в точке![]() ,
необходимо и достаточно, чтобы существовала
производная
,
необходимо и достаточно, чтобы существовала
производная![]() ,
при этом
,
при этом![]() .
(т.е.
.
(т.е.![]() )(см. рис. 15).
)(см. рис. 15).
Формула
для приближенного вычисления значения
функции в точке
![]() имеет вид:
имеет вид:
![]() .
.
Перечислим основные
свойства
дифференциала.
Пусть функции
![]() и
и![]() дифференцируемы, тогда
дифференцируемы, тогда
 ,
где с –
число.
,
где с –
число. .
. ,
если
,
если
 .
.
