§4. Системы линейных алгебраических уравнений (слау). Матричный метод решения

Определение. Системой из m линейных алгебраических уравнений с n неизвестными называется система вида:

(1)

Здесь переменные называютсянеизвестными системы, числа , гденазываютсякоэффициентами системы, а числа – свободными членами.

Числа , обращающие все уравнения системы в тождества, называютсярешением системы. Система, имеющая решение называется совместной, система, не имеющая решений – несовместной.

Обозначим через A матрицу размера , составленную из коэффициентов при неизвестных:A= (матрица системы).

Столбец свободных членов обозначим через B=, а столбец из неизвестных системы черезX = . Тогда систему (1) можно записать в виде матричного уравнения:. Эта запись называетсяматричной формой записи системы (1).

Теорема. Система ЛАУ обладающая квадратной невырожденной матрицей А имеет единственное решение: .

Метод решения СЛАУ с использованием соотношения называетсяматричным методом решения.

§5. Метод Гаусса для исследования и решения слау

Расширенной матрицей СЛАУ называется матрица, полученная из матрицы системы приписыванием справа столбца свободных членов системы:

=.

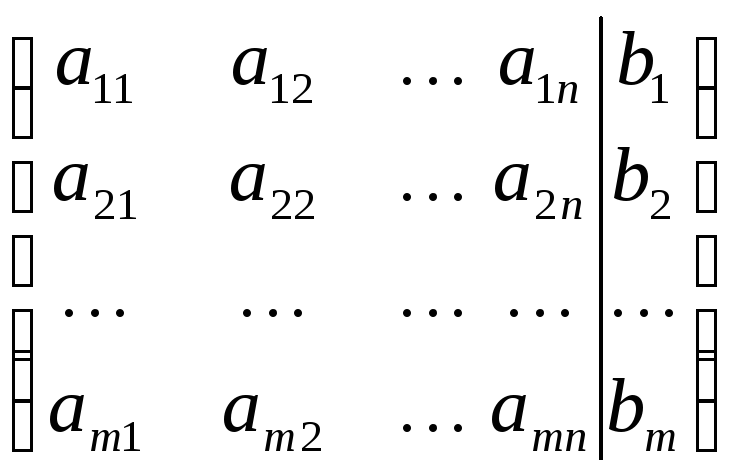Элементарными преобразованиями для матрицы называются следующие её преобразования.

1. Перестановка строк местами.

2. Умножение строки на ненулевой коэффициент.

3. Прибавление к одной строке матрицы другой её строки умноженной на некоторое число .

4. Зачёркивание нулевой строки матрицы.

Метод Гаусса состоит в том, что с помощью элементарных преобразований матрица приводится к верхнетреугольному виду с ненулевыми элементами на главной диагонали.

1. С помощью перестановок строк и столбцов матрицы добиваемся того, чтобы a₁₁ стал отличным от нуля (здесь и в дальнейшем элементы всех матриц будем обозначать в виде a_ij).

2. Прибавим ко второй строке первую, умноженную на . Прибавим к третьей строке матрицы первую умноженную на и так далее. В результате в первом столбце получим нулевые элементы нижеa₁₁.

3. С помощью перестановок строк и столбцов начиная со второй строки и второго столбца добиваемся того чтобы a₂₂0.

4. Прибавим к третьей строке вторую, умноженную на . Прибавим к четвёртой строке матрицы вторую, умноженную наи так далее. В результате во втором столбце получим нулевые элементы нижеa₂₂.

Этот процесс продолжаем до тех пор, пока возможно получение 0 из строк и столбцов начиная с номера .

Окончательно после зачёркивания нулевых строк матрица приводится к виду ~, где все 0.

После приведения матрицы к верхнетреугольному виду, по последней матрице восстанавливаем систему и решаем её, начиная с последнего уравнения. Возможны три случая.

1. Система решений не имеет.

2. Система имеет единственное решение.

3) Система имеет бесконечно много решений, зависящих от нескольких произвольных параметров.

§6. Однородные системы линейных алгебраических уравнений

Система ЛАУ, все свободные члены которой нулевые, называется однородной, иначе неоднородной. В общем случае однородная система из m уравнений с n неизвестными имеет вид AX=0:

.

Однородная система всегда совместна, поскольку она имеет решение , которое называетсятривиальным.

Метод Гаусса для решения однородных систем используется в следующем виде. Записываем матрицу системы A и с помощью элементарных преобразований приводим её к верхнетреугольному виду. Возможны два случая.

1) Система имеет единственное тривиальное решение.

2) Система имеет бесконечно много решений, зависящих от нескольких параметров.