
- •М.Ю. ДУХОН
- •Часть 2
- •МОСКВА – 2005
- •СВОЙСТВА ФУНКЦИЙ
- •Задачи для самостоятельного решения
- •Свойства пределов числовых последовательностей
- •Примеры
- •Свойства бесконечно малых последовательностей
- •Задачи для самостоятельного решения
- •Свойства предела функции
- •Примеры решения задач
- •Раскрытие неопределенностей
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Рекомендованная литература
- •Задачи для индивидуального выполнения
- •Правила дифференцирования
- •Производные основных элементарных функций
- •Логарифмическая функция
- •Показательная функция
- •Обратные тригонометрические функции
- •Производная функции, заданной параметрически
- •Логарифмическое дифференцирование
- •Производные высших порядков
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Связь между монотонностью функции и ее производной
- •Наибольшее и наименьшее значение функции
- •Задачи для самостоятельного решения
- •Свойства неопределенного интеграла
- •Свойства определенного интеграла
- •Непосредственное интегрирование
- •Метод интегрирования по частям
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •ДУХОН Михаил Юльевич
- •Часть 2

Получим:
6 |
3 |
dx |
|
1 |
|
x |
|
|
|
1 |
|
6 3 |
1 |
|
6 |
1 |
|
|
1 |
|
|
|||
∫6 |
|
|
arctg |
6 |
3 |
|
arctg |
arctg |
arctg |
3 − |
arctg1 |
|
||||||||||||
|
|
= |
|
|
|
6 |
|
= |
|
6 |
− |
|
6 |
= |
|
|
= |
|||||||
|
x2 + 36 |
6 |
6 |
|
6 |
6 |
6 |
6 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
= 61 π3 − 61 π4 = 18π − 24π = 72π .
Ответ: 72π .
Метод интегрирования по частям
Формула интегрирования по частям для определенного интеграла имеет вид:
b b
∫u(x)v′(x)dx = u(x) v (x) ba − ∫u′(x) v (x)dx. (3.2.8)
a |
a |
Пример 3.2.4. Найти интеграл: |
|
|
|
|
∫5 |
xexdx. |
|
|
|
|
|
Решение. |
0 |
|
|
|
|
|
|
|
Воспользуемся формулой (3.2.8). |
Пусть |
||||||
u(x)= x; v′(x)= ex . Тогда u′(x)= 1; v (x)= ex . Получим: |
|
|
|
|||||
∫5 |
xex dx = xex |
|
05 − ∫5 1 exdx = 5 e5 −0 e0 − ∫5 exdx = 5e5 −ex |
|
|
05 = |
||
|
|
|||||||
0 |
|
|
0 |
|
0 |
|
|
|
= 5e5 −(e5 −e0 )= 5e5 −e5 + 1 = 4e5 + 1. |
|
|
|
|
||||
|
Ответ: 4e5 + 1. |
|
|
|
|
|
||
Метод замены переменной. Пусть функция |
f (x) непрерывна на |
|||||||
отрезке [a;b] и ϕ (t ) – непрерывно дифференцируема на отрезке
t1 ;t2 , где a = f (t1 ), b = f (t2 ). Тогда
b |
t2 |
|
∫ f (x)dx = ∫ f (ϕ (t ))ϕ′(t )dx. |
(3.2.9) |
|
a |
t1 |
|
190
Такое преобразование определенного интеграла называется
заменой переменной.
Часто удобно вводить новую переменную как функцию старой, т. е. полагать t =ψ (x). Тогда новыми пределами интегрирова-
ния являются числа t1 =ψ (a) и t2 =ψ (b).
Пример 3.2.5. Найти интеграл:
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
x |
|
|
|
|
|
|
|
||
|
∫1 |
3 |
dx. |
|
|
|
|
|
|
|
||||
|
1 + 9x |
|
|
|
|
|
|
|
||||||
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Выполним замену переменной: пусть 3x = t . Тогда |
||||||||||||||
9x = t2 , |
dt = 3x ln 3dx, |
|
|
|
3x dx = |
1 |
dt , |
t1 = 3− |
1 |
= |
1 |
, |
||
|
|
|
2 |
|||||||||||
|
|
|
ln 3 |
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t2 = 3 |
2 |
= |
|
3 . В результате получим: |
|
|
|
||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
||||
|
2 |
|
|
3x |
|
dx |
= |
1 |
|
dt |
= |
1 |
|
dt |
= |
1 |
arctgt |
|
3 |
||||||
∫1 1 + 9x |
ln 3 ∫1 1 + t2 |
ln 3 ∫1 1 + t 2 |
ln 3 |
|
1 |
||||||||||||||||||||
|
|
|
|
|
|
3 |
|||||||||||||||||||
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||
|
1 |
|
|
1 |
|
|
|
= |
|
arctg 3 |
−arctg |
|
|
= |
|
ln 3 |
3 |
||||||
|
|
|
|
|
= |
1 |
|
π |
|
− |
π |
= |
|
π |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
ln 3 |
3 |
6 ln 3 |
|
||||||||||
|
|
|
6 |
|
|
|
|||||||
|
|
|
|
Ответ: |
|
|
π |
. |
|||||
|
|
|
|
|
6 ln 3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 3.2.6. Найти интеграл:
|
|
3 |
|
|
π |
−arcsin x |
|
|
|
2 |
|
|
4 |
||
|
|
∫3 |
|
dx. |
|||
|
|
|
|
||||
− |
|
1 − x2 |
|||||
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
191
|
|
|
|
|
|
|
|
Решение. |
|
|
|
Выполним |
|
|
замену: |
|
|
|
arcsin x = t . |
|
|
|
Тогда |
||||||||||||||||||||||||||||||||||||
dt = (arcsin x)′ dx = |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
π |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
t |
1 |
= arcsin − |
|
|
|
= − |
|
, |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
t2 = arcsin |
|
|
3 |
|
|
= |
π |
. Получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
4 −arcsin x |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
π3 |
|
|
|
|
|
|
|
1 π 2 |
|
||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
π |
|
|
|
|
2 |
|
|
|
|
π |
|
π |
|
|
|||||||||||||||||||||||||||
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
∫ |
|
|
|
− t |
|
dt = |
|
|
|
t − |
|
|
|
t |
|
|
|
|
|
= |
|
|
|
− |
|
|
|
|
− |
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
− |
π |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3 |
|
|
|
|
1 − x |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
4 3 2 |
3 |
|
|
|||||||||||||||||||
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
π |
|
|
|
π |
|
|
1 |
|
|
π |
2 |
|
|
π 2 |
|
π |
2 |
|
|
π 2 |
|
|
|
|
π 2 |
|
|
π 2 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
− |
|
|
|
|
− |
|
|
− |
|
|
|
|
|
− |
|
|
|
|
= |
|
|
|
− |
|
|
+ |
|
|
|
+ |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
4 |
|
|
3 |
|
2 |
|
|
3 |
|
|
|
12 18 12 18 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Ответ: |
π 2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Пример 3.2.7. Найти интеграл: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
π |
− 4 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
3 |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Решение. |
|
|
|
Выполним |
|
|
|
замену: |
|
|
|
|
π |
|
− 4 x = t . |
|
|
|
Тогда |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
π |
|
|||||
dt |
= |
|
4 |
− |
4 x |
dx = −4dx, |
|
|
|
dx = − |
|
|
|
|
dt , |
|
|
|
t1 |
= |
|
|
− |
4 0 = |
|
, |
|||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
3 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
t2 = π3 − 4 24π = π3 − π6 = π6 . Получим:
π |
|
|
|
|
π |
|
|
π |
|
|
|
|
|
|
|
24 |
π |
|
1 |
6 |
|
1 |
6 |
|
1 |
|
|
|
π |
||
∫0 |
tg |
|
− 4 x dx = − |
|
π∫ |
tgtdt = − |
|
π∫ |
tgtdt = |
|
ln |
cos x |
|
π6 |
|
3 |
4 |
4 |
4 |
||||||||||||
|
|
|
|
|
|
|
3 |
||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
π |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
ln |
|
cos |
|
− ln |
cos |
|
|
|
= |
|
4 |
6 |
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
ln |
|
|
− ln |
|
|
|
|
= |
|
ln |
3 = |
|
ln 3. |
|
4 |
2 |
2 |
4 |
8 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
192
Ответ: 81 ln 3.
Вычисление площадей плоских фигур. Пусть функция f (x) не-
отрицательна на отрезке [a;b]. Площадь криволинейной трапеции,
ограниченной кривой |
y = f (x), прямыми x = a и |
x = b ( a < b ), а |
||
также осью абсцисс, равна: |
|
|
|
|
|
S = ∫b |
f (x)dx. |
|
(3.2.10) |
|
a |
|
[a;b] удовлетворяет усло- |
|
Если функция |
f (x) на отрезке |
|||
вию f (x)≤ 0 , то площадь криволинейной трапеции можно найти по формуле:
S = ∫b |
|
f (x) |
|
dx = −∫b |
f (x)dx. |
(3.2.11) |
|
|
|||||
a |
|
|
|
a |
|
|
Площадь фигуры, ограниченной двумя непрерывными кри- |
||||||
выми y = f1 (x) и y = f2 (x), и двумя прямыми |
x = a и x = b |
|||||
(a < b), где f1 (x)≥ f2 (x) на отрезке [a;b], находится по формуле:
S = ∫b ( f1 (x)− f2 (x))dx. |
(3.2.12) |
a |
|
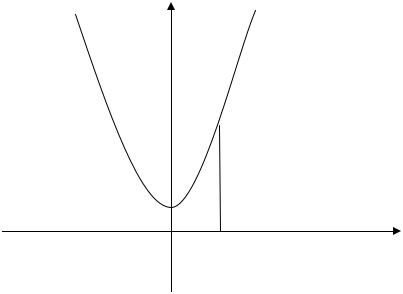
Пример 3.2.8. Найти площадь фигуры, ограниченной параболой y = x2 + 1, прямыми x = −1 и x = 2 , а также осью абсцисс.
Решение. Рассмотрим фигуру, площадь которой мы ищем
(рис. 3).
193
y
y = x2 + 1
 x −1 O 2
x −1 O 2
Рис. 3.2.3
Воспользуемся формулой (3.2.10).
|
|
2 |
2 |
|
|
1 |
|
3 |
|
|
|
|
2 |
1 |
|
3 |
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
S = ∫(x |
|
+ 1)dx = |
|
x |
|
+ x |
|
|
−1 = |
|
2 |
|
+ 2 − |
|
(−1) |
|
+(−1) = |
||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
−1 |
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
= |
8 |
+ 2 + |
1 |
+ 1 = 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
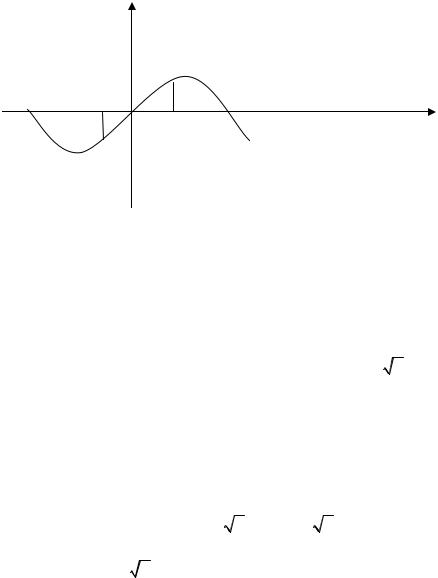
Пример 3.2.9. Найти площадь фигуры, ограниченной кривой |
|||||||||||||||||||||
y = sin x, прямыми x = −π |
, |
|
x = |
π и осью абсцисс. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
Решение. Рассмотрим |
|
фигуру, |
площадь которой |
мы |
ищем |
||||||||||||||||
(рис. 4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
194
y
−π4
O |
π |
y = sin x |
x |
|
3 |
||
|
|
|
Рис. 3.2.4
Очевидно, фигура состоит из двух частей – на отрезке
|
− |
π |
;0 |
|
функция отрицательна, на отрезке |
|
π |
– положительна. |
|
|
4 |
|
0; |
3 |
|
||||
|
|
|
|
|
|
|
|
||
Найдем площади этих фигур отдельно.
1) Первую из них вычислим по формуле (3.2.11).
S1 = − ∫0 |
sin xdx = cos x |
0 |
π |
|
− |
π |
|
− |
4 |
4 |
|
|
|
|
|
|
|
π |
|
2 |
|
||
= cos 0 |
−cos |
− |
|
|
= 1 − |
|
. |
|
4 |
2 |
|||||||
|
|
|
|
|
|
|||
2) Площадь второй фигуры найдем по формуле (3.2.10).
π |
|
|
|
|
|
|
|
|
|
S2 = ∫3 |
|
π |
π |
|
1 |
|
1 |
|
|
sin xdx = −cos x |
03 = −cos |
+ cos 0 = − |
+ 1 = |
. |
|||||
3 |
2 |
2 |
|||||||
0 |
|
|
|
|
|
Площадь искомой фигуры равна сумме найденных площадей.
|
S = |
S1 + S2 = 1 − |
2 |
+ |
1 |
= |
3 − 2 |
. |
|
|
2 |
2 |
2 |
||||||
|
|
|
|
|
|
|
|||
Ответ: |
3 − |
2 |
. |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
195
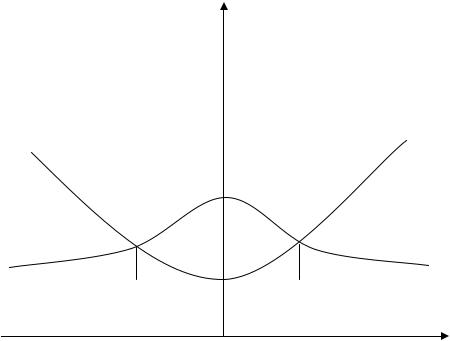
Пример 3.2.10. Найти площадь фигуры, ограниченной кривы-
ми y = |
x2 |
и |
y = |
1 |
. |
|
2 |
1 + x2 |
|||||
|
|
|
|
Решение. Рассмотрим фигуру, площадь которой мы ищем
(рис. 5).
y
−1 |
О |
1 |
Рис.3.2.5
Для вычисления площади фигуры воспользуемся формулой (3.2.12). Найдем сначала абсциссы точек пересечения кривых. Для этого следует решить уравнение
|
|
|
|
1 |
= |
x2 |
. |
|
|
|
|
x2 |
|
1 + x2 |
2 |
||
|
|
|
|
|
|
|||
1 |
|
= |
(1 + x2 )x2 |
= 2 x4 + x2 − 2 = 0. |
||||
1 + x |
2 |
|
||||||
|
2 |
|
|
|
|
|
||
196

|
Корнями этого уравнения являются числа |
x1 = −1 и |
x2 |
= 1. |
|||||||||||||||||
Теперь можно воспользоваться формулой (3.2.12). |
|
|
|
|
|
|
|||||||||||||||
1 |
|
1 |
|
|
x2 |
|
|
1 |
|
3 |
|
|
1 |
|
|
|
1 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
S = |
|
|
|
− |
|
dx = arctgx − |
|
x |
|
|
|
−1 |
= |
arctg1 − |
|
|
|
− |
|||
|
2 |
|
|
|
|
|
|||||||||||||||
−∫1 |
1 + x |
|
|
2 |
|
|
6 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
−arctg (−1)− 61 (−1)3 = π4 − 61 − −π4 + 61 =
=π4 − 61 + π4 − 61 = π2 − 31 .
Ответ: π2 − 13 .
Вычисление объема тела вращения. Объем тела, образован-
ного вращением вокруг оси Ox криволинейной трапеции, ограниченной непрерывной кривой y = f (x), осью абсцисс и прямыми x = a
и x = b (a < b), находится по формуле
V = π ∫b ( f (x))2 dx. |
(3.2.13) |
a |
|
Объем тела, образованного вращением вокруг оси Oy криволинейной трапеции, ограниченной непрерывной кривой x =ϕ (y),
осью ординат и прямыми y = c и y = d (c < d ), находится по формуле
V = π ∫d (ϕ (y))2 dy. |
(3.2.14) |
c
Пример 3.2.11. Вычислить объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной гипер-
болой y = 4x , прямыми x = 3, x = 12 и осью абсцисс.
Решение. Воспользуемся формулой (3.2.13).
197

|
12 |
|
4 |
2 |
|
12 |
16 |
|
12 |
dx |
|
16π |
|
12 |
16π |
|
|
16π |
|
||||||||||||
V = π |
∫3 |
dx =π |
∫3 |
dx =16π |
∫3 |
|
|
|
|
= 4π . |
|||||||||||||||||||||
|
|
|
|
2 |
|
|
2 = − |
|
|
|
|
3 = − |
|
+ |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
x |
|
|
x |
|
|
x |
|
|
|
x |
|
|
|
12 |
|
|
3 |
|
|||||||||||
|
Ответ: 4π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Пример 3.2.12. Найти объем тела, образованного вращением |
||||||||||||||||||||||||||||||
кривой |
y = |
x2 |
вокруг оси ординат в пределах от y = 1 до |
y = 5 . |
|||||||||||||||||||||||||||
4 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. Уравнение кривой |
|
y = |
|
равносильно |
|
|
x |
|
= 2 y . |
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
||||||||||||||||||||||||
Воспользуемся формулой (3.2.14). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
V = π ∫5 (2 |
|
y )2 dy =π ∫5 |
4 ydy =2π y2 |
|
|
15 |
= 2π 52 − 2π 12 |
= 50π − 2π = 48π . |
|||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 48π .
Пример 3.2.13. Воспользуемся формулой (3.2.13), чтобы вывести известную нам из школьного курса стереометрии формулу объема прямого кругового конуса
V = 13 π R2 H ,
где R – радиус основания, H – высота. Конус, имеющий перечисленные параметры, образуется при вращении вокруг оси абсцисс тре-
угольника, ограниченного прямыми y = HR x, x = H , а также осью
абсцисс (рис. 6). Этот треугольник является криволинейной трапецией и, следовательно, для вычисления объема тела вращения можно воспользоваться формулой (3.2.13).
198
