
- •М.Ю. ДУХОН
- •Часть 2
- •МОСКВА – 2005
- •СВОЙСТВА ФУНКЦИЙ
- •Задачи для самостоятельного решения
- •Свойства пределов числовых последовательностей
- •Примеры
- •Свойства бесконечно малых последовательностей
- •Задачи для самостоятельного решения
- •Свойства предела функции
- •Примеры решения задач
- •Раскрытие неопределенностей
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Рекомендованная литература
- •Задачи для индивидуального выполнения
- •Правила дифференцирования
- •Производные основных элементарных функций
- •Логарифмическая функция
- •Показательная функция
- •Обратные тригонометрические функции
- •Производная функции, заданной параметрически
- •Логарифмическое дифференцирование
- •Производные высших порядков
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Связь между монотонностью функции и ее производной
- •Наибольшее и наименьшее значение функции
- •Задачи для самостоятельного решения
- •Свойства неопределенного интеграла
- •Свойства определенного интеграла
- •Непосредственное интегрирование
- •Метод интегрирования по частям
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •ДУХОН Михаил Юльевич
- •Часть 2
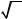
Пример 2.1.20. Найти вторую и третью производные функции f (x)= 3x4 −5 x2 + 2 x −7.
Решение.
f ′ (x)= (3x4 −5 x2 + 2 x −7 )′ = 12 x3 −10 x + 2. f ′′(x)= (12 x3 −10 x + 2)′ = 36 x2 −10.
f ′′′(x)= (36 x2 −10)′ =72 x.
Пример 2.1.21. Найти вторую и третью производные функции f (x)= x2 sin x.
Решение.
f ′ (x)= (x2 sin x)′ = (x2 )′ sin x + x2 (sin x)′ = 2 x sin x + x2 cos x. f ′′(x)= (2 x sin x + x2 cos x)′ = (2x sin x)′ +(x2 cos x)′ =
= 2 sin x + 2 x cos x + 2 x cos x − x2 sin x = 2 sin x + 4 x cos x − x2 sin x. f ′′′(x)= (2 sin x + 4 x cos x − x2 sin x)′ = 2 cos x + 4 cos x −
−4 x sin x − 2 x sin x − x2 cos x = 6 cos x −6 x sin x − x2 cos x.
Задачи для самостоятельного решения |
|
|
|
|
|
||
Найти производные функций: |
|
|
|
|
|||
2.1.1. |
f (x)= 2 x4 |
− 3x2 |
+ 5 x −7. |
||||
2.1.2. |
f (x)= 5 x3 |
− 4 x2 |
+7 x − |
1 |
. |
||
|
|
|
|||||
|
|
|
|
|
1 |
x |
|
2.1.3. |
f (x)= 4 x4 |
− 3x3 |
+ 2 x − |
|
. |
|
|
|
|
||||||
|
|
|
|
|
x |
||
74

2.1.4.f (x)=7 ,5 x4 −5 x2 − x12 .
2.1.5.f (x)= 8 x3 + 3x2 −5 x − 1x .
2.1.6. |
f (x)= 9 x4 |
−5 x2 |
+ 3x − 2 x . |
|||||
2.1.7. |
f (x)=7 x4 |
−5 x3 |
+ 4 x − |
|
1 |
. |
||
|
||||||||
|
|
|
|
|
|
x |
||
2.1.8. |
f (x)= 9 x3 |
+ x2 −6 x − |
|
1 |
. |
|||
|
|
|||||||
|
|
|
|
|
|
x |
||
2.1.9.f (x)= 12 x3 −6 x2 + 5 x − x12 .
2.1.10.f (x)=7 x4 +6 x3 −5 x − 1x .
2.1.11.f (x)=7 x3 −6 x2 + 11x − 2x .
2.1.12. |
f (x)= 9 x4 |
−7 x3 + 2 x2 − 3 |
x . |
||
2.1.13. |
f (x)= 5 x3 |
−12 x2 + 3 − |
1 |
. |
|
x |
|||||
|
f (x)= 2 x5 |
|
|
||
2.1.14. |
− 3x2 + 5 x − 2 |
x . |
|||
2.1.15.f (x)= 4 x3 − x2 + 2x .
2.1.16.f (x)= 8 x4 −7 x3 −1 + 1x .
2.1.17. |
f (x)= 2 x7 |
− 3x4 + x2 |
− |
x . |
|
2.1.18. |
f (x)= 4 x5 |
+ x4 − 2 x + |
x . |
||
2.1.19. |
f (x)= 5 x6 |
− x5 + 3x4 |
− |
1 |
. |
|
|||||
|
|
|
|
x2 |
|
75
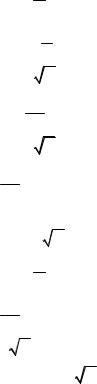
2.1.20.f (x)= 9 x3 −5 x2 + 3x − 1x .
2.1.21.f (x)= 11x4 − 3x2 + 5 x − 1x .
2.1.22. f (x)= 9 x6 − 3x4 + 2 x + x .
2.1.23.f (x)= 4 x7 − 3x4 + x − x12 .
2.1.24.f (x)= 6 x4 + 3x3 −5 x + 3 x .
2.1.25.f (x)=7 x5 − 2 x4 + x12 .
2.1.26. f (x)= 10 x3 −5 x2 +7 x − |
1 |
. |
|
||
|
x |
|
2.1.27.f (x)= 6 x4 +7 x3 −5 x + 1x .
2.1.28.f (x)= 8 x4 −5 x3 + x12 .
2.1.29. |
f (x)= 2 x6 |
−5 x3 |
+ 2 x . |
2.1.30. |
f (x)= 4 x3 |
−7 x2 |
+ +5 x − 3 − 4 x . |
2.1.31.f (x)= 3 sin x −5 cos x.
2.1.32.f (x)= 2tgx − 4 cos x.
2.1.33.f (x)= 3 arcsin x + 2arccosx.
2.1.34.f (x)= 3x − 2x .
2.1.35.f (x)= 2tgx −5 sin x.
2.1.36.f (x)= 3ctgx + 2 cos x.
2.1.37.f (x)= 3x + 2 cos x.
2.1.38.f (x)= 5 cos x + ctgx.
76
2.1.39. f (x)= 4 sin x + 3 cos x. 2.1.40. f (x)= 2tgx + 3ctgx. 2.1.41. f (x)= 4 x − 3tgx.
2.1.42. f (x)= 2 arcsin x + 5arccosx. 2.1.43. f (x)= 9 cos x + 2 log3 x. 2.1.44. f (x)= 4 sin x − ln x.
2.1.45. f (x)= 5 sin x − 4tgx. 2.1.46. f (x)= 3tgx + log2 x. 2.1.47. f (x)= 5ctgx − log5 x. 2.1.48. f (x)= 3 cos x + 5 ln x.
2.1.49. f (x)= 5x − lg x
2.1.50. f (x)= arcsin x + 2arccosx. 2.1.51. f (x)= 3 ln x −5 cos x. 2.1.52. f (x)= 9 sin x − 2tgx. 2.1.53. f (x)= 3tgx − 2arctgx. 2.1.54. f (x)= 3x −5arctgx. 2.1.55. f (x)= 4 cos x −6ctgx.
2.1.56. f (x)= ex + ln x.
2.1.57. f (x)= 4 arcsin x −5arccosx. 2.1.58. f (x)= 3 sin x + 2 cos x. 2.1.59. f (x)= 2arctgx − 3arcctgx. 2.1.60. f (x)= log2 x + 4tgx.
2.1.61. f (x)= 1 + ex . 1 −ex
77
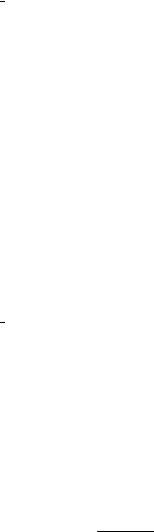
2.1.62. |
f (x)= |
1 + 2x . |
|
||
|
|
cos x |
|
||
2.1.63. |
f (x)= |
1 −cos x . |
|||
|
|
|
sin x |
|
|
2.1.64. |
f (x)= |
|
sin x |
. |
|
1 |
+ sin x |
||||
|
|
|
|||
2.1.65. |
f (x)= |
1 |
+ sin x . |
||
|
|
|
cos x |
|
|
2.1.66. |
f (x)= |
1 |
− sin x . |
||
|
|
|
cos x |
|
|
2.1.67.f (x)= ex sin x.
2.1.68.f (x)= ex cos x.
2.1.69.f (x)= x2 sin x.
2.1.70.f (x)= x3 cos x.
2.1.71.f (x)= x2 arcsin x.
2.1.72.f (x)= x2arccosx.
2.1.73.f (x)= x2 ln x.
2.1.74.f (x)= x3 lg x.
2.1.75.f (x)= ex tgx.
2.1.76.f (x)= (1 + x2 )sin x.
2.1.77.f (x)= x3ctgx.
2.1.78.f (x)= x2arctgx.
2.1.79.f (x)= 1 − 2x .
1+ 2x
2.1.80.f (x)= 1 +coscosx x .
78

2.1.81.f (x)= 6 x arctgx.
2.1.82.f (x)= elnx −x2 .
2.1.83.f (x)= extgx− x .
2.1.84. |
f (x)= cos x . |
||||
|
|
ex |
|||
2.1.85. |
f (x)= |
7 x − 3 . |
|||
|
|
sin x |
|||
2.1.86. |
f (x)= |
9x −1 . |
|||
|
|
9x + 1 |
|||
2.1.87. |
f (x)= |
1 + 4 sin x |
. |
||
|
|
|
|||
|
|
2 − 3 cos x |
|||
2.1.88. |
f (x)= |
3 cos x . |
|||
|
|
2 x + 1 |
|||
2.1.89. |
f (x)= |
x2 + 2 x |
. |
||
|
|
||||
|
|
3 − 4 x |
|||
2.1.90. |
f (x)= |
5 x2 |
. |
||
|
|||||
|
|
x − 3 |
|||
2.1.91.f (x)= sin(3x −1).
2.1.92.f (x)= (5 x − 2)4 .
2.1.93.f (x)= (3x2 + 1)3 .
2.1.94.f (x)= 2 sin(5 x − 2).
2.1.95.f (x)= arcsin 3x .
2.1.96. f (x)= x2 + 4 . 2.1.97. f (x)= 105−3 x .
79

2.1.98. f (x)= ln3 x.
|
1 |
|
|
|
|
2.1.99. f (x)= 2 |
|
. |
|
|
|
x |
|||||
2.1.100. f (x)= ex −1. |
|||||
2.1.101. f (x)= ecos x . |
|||||
2.1.102. |
f (x)= esin x . |
||||
2.1.103. |
f (x)= sin |
1 |
. |
||
|
|||||
|
|
|
|
x2 |
|
2.1.104. f (x)=7e− x2 . |
|||||
2.1.105. f (x)= arctg (ln x).
2.1.106. f (x)= 1 −ex . 2.1.107. f (x)= 5 x2 −3 x+1 . 2.1.108. f (x)= 34−x2 .
2.1.109. f (x)= earccosx . 2.1.110. f (x)= ex3 .
2.1.111. f (x)= (3x2 −1)6 . 2.1.112. f (x)= sin4 x. 2.1.113. f (x)= cos3 x. 2.1.114. f (x)= tg3 x.
2.1.115. f (x)= arctgx2 .
2.1.116. f (x)= ln3 x. 2.1.117. f (x)= 3x3 +1 . 2.1.118. f (x)= etgx .
80
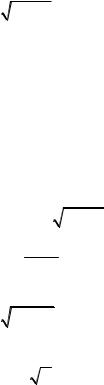
2.1.119. f (x)= ectgx . 2.1.120. f (x)= cos 2x .
2.1.121. f (x)= |
x3 + 1. |
2.1.122. f (x)= ln cos x. |
|
2.1.123. f (x)= lnsin x. |
|
2.1.124. f (x)= earcsin x . |
|
2.1.125. f (x)= tgx4 . |
|
2.1.126. f (x)= sin6 x. |
|
2.1.127. f (x)= 1 |
− sin 2x . |
1 |
+ sin 2 x |
2.1.128. f (x)= (x − 2) x2 + 1.
2.1.129. f (x)= cos x x+ 1 .
2.1.130. f (x)= e−x ln tgx. 2.1.131. f (x)= arctgx . 2.1.132. f (x)= arccos3 x.
2.1.133. f (x)= (1 + 3 x )3 . 2.1.134. f (x)= sin x ecos x . 2.1.135. f (x)= sin ex .
2.1.136. f (x)= 3sin x . 2.1.137. f (x)= x2 x . 2.1.138. f (x)= xln x .
2.1.139. f (x)= ln tgx.
81

2.1.140. f (x)= (1 + ln x)4 .
2.1.141. f (x)= e
2.1.142. f (x)= arctgx3 .
2.1.143. f (x)= cos3 4 x.
2.1.144. f (x)= sin 1x .
2.1.145. f (x)= arct1gx .
2.1.146. f (x)= (x3 + 2 x)4 .
2.1.147. f (x)= (2 sin x − 3 cos x)4 .
2.1.148. f (x)= tg2 5 x. 2.1.149. f (x)= esin2 x .
2.1.150. f (x)= arccosex .
82
2.2. МЕХАНИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Геометрический смысл производной. Пусть дана функция и точка M (x0 , y0 ) на ее графике. Если в точке М к графику
функции f (x) проведена касательная, уравнение которой имеет вид
y = kx + b , пусть эта касательная образует с положительным направлением оси абсцисс угол α . Тогда тангенс угла α равен значению производной функции f (x) в точке касания и равен также коэффициенту k в уравнении касательной, то есть
tgα = f ′(x0 )= k . |
y = f (x) |
(2.2.1) |
||
Уравнение касательной к графику функции |
в точ- |
|||
ке M (x0 , y0 ) имеет вид: |
|
|
|
|
y = f (x0 )+ f ′(x0 )(x − x0 ) |
|
(2.2.2) |
||
Уравнение нормали, т. е. прямой, проходящей через точку ка- |
||||
сания M (x0 , y0 ) перпендикулярно касательной, имеет вид: |
|
|||
y = f (x0 )− |
1 |
(x − x0 ) |
|
(2.2.3) |
f ′(x0 ) |
|
|||
|
|
|
|
|
Пример 2.2.1. Составить уравнение касательной к графику |
||||
функции y = 2 x2 + 3x −1 в точке с абсциссой x0 = 2. |
|
|||
Решение. Найдем значение функции в точке x0 = 2. |
|
|||
f (2)= 2 22 + 3 2 −1 = 13. |
|
|
||
Найдем производную функции f (x): |
|
|
||
f ′(x)= (2x2 + 3x −1)′ = 4 x + 3. |
f (x) в |
|
||
Найдем значение производной |
функции |
точке |
||
x0 = 2 : f ′(2)= 4 2 + 3 = 11. |
|
|
|
|
83

Воспользуемся формулой (2.2.2):
y = 13 + 11(x − 2)
или
y = 11x −9.
|
|
Пример 2.2.2. Составить уравнения касательной и нормали к |
|||||||||||||||||||
графику функции |
y = |
x −1 |
в точке с абсциссой x0 |
= −1. |
|
|
|
|
|
||||||||||||
x + 2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Найдем значение функции в точке x0 = −1. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
f (−1)= |
−1 −1 |
|
= −2. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
−1 + 2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Найдем производную функции f (x): |
|
|
|
|
|
|
|
|
|||||||||||
|
|
x −1 |
′ |
(x −1)′ (x + 2)−(x −1)(x + 2)′ |
x + 2 − x +1 |
|
|
3 |
|
|
|||||||||||
f |
′(x)= |
|
= |
|
|
|
|
|
|
2 |
|
= |
|
|
|
= |
|
|
|
. |
|
|
|
|
|
(x + 2) |
|
(x + 2) |
2 |
(x + 2) |
2 |
||||||||||||
|
|
x + 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Найдем значение |
производной |
функции |
f (x) |
в |
точке |
||||||||||||||
x |
|
= −1 : f ′(−1)= |
|
3 |
|
= 3. |
|
|
|
|
|
|
|
|
|
|
|||||
0 |
(−1 + 2)2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Воспользуемся для составления уравнения касательной фор-
мулой (2.2.2):
y = −2 + 3(x + 1)
или
y = 3x + 1.
Воспользуемся для составления уравнения нормали форму-
лой (2.2.3):
y = −2 − 13 (x + 1)
или
y = − 13 x −73 .
84

Пример 2.2.3. В каких точках касательная к графику функции y = 13 x3 − x2 − x + 1 параллельна прямой y = 2 x − 3 ?
Решение. Условием параллельности прямых y = k1 x + b1 и y = k2 x + b2 является равенство их угловых коэффициентов k1 = k2 . Угловой коэффициент k1 прямой y = 2 x − 3 равен 2. В соответствии с геометрическим смыслом производной (формула (2.2.1.)) угловой
коэффициент |
k2 |
|
касательной |
|
к |
|
графику |
функции |
|||||||||||
y = |
1 |
x3 − x2 |
− x + 1 в точке |
x0 |
равен значению производной этой |
||||||||||||||
|
|||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции в точке x0 . Найдем производную функции. |
|
||||||||||||||||||
|
|
|
|
|
1 |
|
|
3 |
|
2 |
|
|
|
|
′ |
2 |
|
|
|
|
|
|
f ′(x)= |
|
x |
|
− x |
|
− x + 1 = x |
|
− 2 x −1. |
|
|||||||
|
|
|
3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соответственно, значение производной этой функции в точке |
||||||||||||||||
x0 |
равно: f ′(x0 )= x0 |
2 − 2 x0 −1. |
|
|
|
|
|
|
|
||||||||||
|
|
|
Таким образом, |
k |
1 |
= 2 |
и |
k |
2 |
= x 2 − 2 x |
−1. Поэтому усло- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
||
вие параллельности выглядит так: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x |
2 − 2 x |
0 |
−1 = 2. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
Решениями этого |
|
уравнения |
являются |
числа |
x01 = −1 и |
|||||||||||
x02 |
= 3 . Соответствующие значения функции равны: |
|
|||||||||||||||||
f (−1)= 13 (−1)3 −(−1)2 −(−1)+ 1 = − 13 −1 + 1 + 1 = 23 . f (3)= 13 33 − 32 − 3 + 1 = 9 −9 − 3 + 1 = −2.
Таким образом, касательные параллельны графику функции в
|
−1; |
2 |
|
и B (3;−2). |
точках A |
3 |
|
||
|
|
|
|
85

Пример 2.2.4. В каких точках касательная к графику функции f (x)= 13 x3 − 52 x2 +7 x − 4 образует с положительным направле-
нием оси абсцисс угол 45°?
Решение. В соответствии с геометрическим смыслом производной (формула (2.2.1)) тангенс угла, который касательная образует с положительным направлением оси абсцисс, равен значению произ-
водной в точке касания. Найдем производную функции f (x).
|
1 |
|
|
5 x2 |
′ |
|
|
f ′ (x)= |
x3 |
− |
+7 x − 4 |
= x2 −5 x +7. |
|||
|
|||||||
3 |
|
2 |
|
|
|||
Пусть искомой точкой касания является точка M (x0 , y0 ). Тогда значение производной в точке М равно:
f ′ (x0 )= x0 2 −5 x0 +7.
Таким образом, в соответствии с геометрическим смыслом производной
|
|
|
|
x 2 −5 x |
0 |
+7 = tg45° |
|
|
|
|
|||||
или |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
x 2 −5 x +7 = 1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
Корнями этого уравнения являются числа x01 = 2 и x02 = 3 . |
|||||||||||||||
Найдем соответствующие значения функции. |
|
|
|
|
|||||||||||
f (2)= |
1 |
|
23 − |
5 |
22 +7 2 − 4 = |
8 −10 + 14 − 4 = |
8 . |
||||||||
3 |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|||
f (3)= |
1 |
|
33 − |
5 |
32 +7 3 − 4 = 9 − 45 |
+ 21 − 4 = |
7 . |
||||||||
3 |
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|||
Касательные образуют с положительным направлением оси |
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
абсцисс угол 45° в точках |
M1 2; 2 |
|
и |
M2 3; 3 |
|
. |
|
||||||||
3 |
2 |
|
|||||||||||||
Пример |
|
2.2.5. |
|
|
|
|
|
|
|
|
|
||||
|
|
Доказать, |
|
что |
на |
графике |
функции |
||||||||
y = x3 + x2 + 2 x −1 нет точек, |
|
в которых касательная была бы па- |
|||||||||||||
раллельна оси абсцисс. |
|
|
|
|
|
|
|
|
|
|
|
||||
86
Решение. Утверждение, что прямая параллельна оси абсцисс равносильно условию, что угол между ними равен нулю, а следовательно, тангенс этого угла равен нулю. Пусть такой точкой является
точка M (x0 , y0 ).
смыслом производной (формула (2.2.1)) в точке x0 производная функции f (x) должна равняться нулю. Найдем производную функ-
ции f (x).
f ′(x)= (x3 + x2 + 2 x −1)′ = 3x2 + 2 x + 2.
Поскольку дискриминант квадратного трехчлена
3x2 + 2 x + 2 отрицателен, ни при каком значении переменной x квадратный трехчлен не равен нулю, а следовательно, производная ни в одной точке не равна нулю, что означает, что ни в одной точке касательная не параллельна оси абсцисс, что и требовалось доказать.
Пример 2.2.6. Составить уравнение касательной к кривой, заданной параметрически
x = t2 −1,
y = t2 + t − 3
в точке M (3;−1).
Решение. Найдем значение параметра t, соответствующее точке М. Это значение должно удовлетворять системе уравнений
|
2 |
−1 |
= 3, |
|
2 |
= 4, |
t |
|
t |
|
|||
|
2 + t − 3 = −1; |
|
2 + t − 2 = 0. |
|||
t |
t |
|||||
|
|
|
|
|
|
|
Корнями первого уравнения являются числа t1,2 = ±2; кор-
нями второго – числа -2 и 1. Таким образом, решением системы является значение параметра t = −2.
Найдем производные функций x (t ) и y (t ). xt′ (t )= (t2 −1)′ = 2t ,
87
yt′ (t )= (t2 + t − 3)′ = 2t + 1.
Угловой коэффициент касательной к кривой в точке М равен
|
|
y′ = |
yt′ |
= |
2t + 1 . |
|
|
|
|
|
|
||||||
xt′ |
|
|
|
|
|
|
|||||||||||
|
|
x |
|
|
|
2t |
|
|
|
|
|
|
|
|
|||
Следовательно |
|
2 (−2)+ 1 |
|
|
|
|
|
|
|
||||||||
|
yx′ (−2)= |
|
= |
3 |
. |
|
|
||||||||||
|
|
|
|
|
|
4 |
|
||||||||||
|
|
|
|
|
2 (−2) |
|
|
|
|
|
|
|
|||||
Воспользуемся формулой (2.2.2). |
|
|
|
|
|
|
|
|
|||||||||
y = −1 + |
3 |
(x − 3)= −1 + |
3 |
x − |
9 |
= |
3 |
x − |
13 . |
||||||||
|
|
4 |
4 |
||||||||||||||
4 |
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|||||
Уравнение касательной |
|
y = |
3 |
x − |
13 . |
|
|
|
|
|
|||||||
|
4 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||
Механический смысл производной. Производная f ′ (x0 )
функции y = f (x), вычисленная при значении аргумента x0 , пред-
ставляет собой скорость изменения этой функции относительно не-
зависимой переменной x в точке x0 .
В частности, пусть прямолинейное движение материальной точки задано формулой
S = S (t ),
где S – пройденный путь; t – время движения. Тогда мгновенная точки (т. е. скорость точки в момент времени t ) равна
производной функции S (t ), то есть |
|
V (t )= S′ (t ). |
(2.2.4) |
Мгновенное ускорение a (t ) точки (т. е. ускорение точки в момент времени t ) равно производной функции V (t ) или второй производной функции S (t ) то есть
88

a (t )=V ′ (t )= S′′(t ). |
(2.2.5) |
Пример 2.2.7. Прямолинейное движение материальной точки задано формулой
S (t )= t3 + 2t2 + 4t −1,
где S – пройденный путь (в метрах); t – время движения (в секундах). Найти скорость и ускорение точки через 3 секунды после начала движения.
Решение. В соответствии с формулой (2.2.4) мгновенная скорость V (t ) точки равна
V (t )= S′ (t )= (t3 + 2t 2 + 4t −1)′ = 3t2 + 4t + 4.
Скорость точки через 3с. после начала движения равна
V (3)= 3 32 + 4 3 + 4 = 43.
Скорость равна 43м / с.
В соответствии с формулой (2.2.5) мгновенное ускорение a (t ) точки равно
a (t )=V ′ (t )= (3t2 + 4t + 4)′ = 6t + 4.
Ускорение точки через 3с. после начала движения равно a (3)= 6 3 + 4 = 22.
Ускорение равно 22м / с2 .
Пример 2.2.8. Прямолинейное движение материальной точки задано формулой
S (t )= 21 t4 −5t3 + 12t2 + 4t − 2,
где S – пройденный путь (в метрах); t – время движения (в секундах). В какие моменты времени ускорение движения точки равно нулю?
Решение. В соответствии с формулой (2.2.5) мгновенное ускорение точки равно
89
a (t )=V ′ (t )= S′′(t ) |
= |
1 |
t4 |
− 5t3 + 12t |
2 + 4t − 2 ′′ |
= (2t3 − 15t 2 |
+ 24t + 4)′ = 6t2 |
− 30t + 24. |
|
||||||||
Приравняв a (t ) |
2 |
|
|
|
|
|
||
к нулю, получим уравнение |
|
|
||||||
6t2 − 30t + 24 = 0 t2 −5t + 4 = 0.
Корнями этого уравнения являются числа t1 = 1, t2 = 4.
Ускорение точки равно нулю через 1с. и через 4с. после начала движения.
Дифференциал функции. Пусть функция y = f (x) диффе-
ренцируема в точке x , то есть y = f ′(x) x +αΔx, где α – бесконечно малая при x → 0 . Тогда главная линейная часть прираще-
ния функции, т. е. |
f ′(x) |
x называется дифференциалом функции |
||||||
f (x) в |
точке |
x |
и |
обозначается |
df (x) или |
dy |
или |
|
dy = f ′(x) |
x. |
|
|
|
|
|
|
|
Пример 2.2.9. Найти дифференциалы функций |
|
|
||||||
1 ).y = x2 , |
|
|
|
|
|
|
|
|
2 ). y = x3 , |
|
|
|
|
|
|
|
|
3 ).y = sin x. |
|
|
|
|
|
|
||
Решение. 1) |
dy = f ′(x) |
x = 2x |
x. |
|
|
|||
2) dy = f ′(x) x = 3x2 x. |
|
|
|
|||||
3) dy = f ′(x) |
x = cos x |
x. |
|
|
|
|||
Геометрический смысл дифференциала состоит в |
том, |
что |
||||||
дифференциал dy в точке x0 есть приращение ординаты касательной при переходе от точки x0 к точке x0 + x .
90

|
Для дифференцируемой в точке x0 функции |
f (x) справед- |
|||
ливо |
приближенное |
равенство |
y ≈ dy . |
Полагая, |
что |
y = f (x)− f (x0 ), |
x = x − x0 , получим: |
|
|
||
f (x)− f (x0 )≈ f ′(x0 )(x − x0 ),
или
f (x)≈ f (x0 )+ f ′(x0 )(x − x0 ), (2.2.6)
Приближенное равенство (2.2.6) можно использовать в приближенных вычислениях. Для того, чтобы найти приближенное зна-
чение функции f (x) в точке x , нужно:
1.Найти достаточно близкое к x значение аргумента x0 , для которого значение f (x0 ) было бы вычислить достаточно легко.
2.Вычислить f (x0 ).
3.Найти производную f ′(x).
4.Найти значение производной функции в точке x0 . |
|
|||||||||
5. Подставить x , а также |
вычисленные |
значения |
x0 , |
|||||||
f (x0 ), f ′(x0 ) |
в формулу (2.2.6). |
|
|
|
|
|
|
|
|
|
Пример 2.2.10. Вычислить |
4,03 |
с точностью до 0,001. |
|
|||||||
Решение. |
Рассмотрим функцию |
f (x)= x . |
Пусть x0 |
= 4, |
||||||
тогда f (x0 )= |
4 = 2. Найдем производную функции f (x). |
|
||||||||
|
f ′(x)= ( |
x )′ = |
1 |
. |
|
|
||||
|
2 x |
|
|
|||||||
Тогда f ′(x0 )= f ′(4)= |
|
1 |
= |
|
1 |
. |
|
|
|
|
|
4 |
|
4 |
|
|
|
||||
|
2 |
|
|
|
|
|
|
|||
f (4,03)≈ f (4)+ f ′(4)(4,03 − 4)= 2 + 41 0,03 = 2,0075 ≈ 2,008.
Ответ: 2,008.
91
