
- •М.Ю. ДУХОН
- •Часть 2
- •МОСКВА – 2005
- •СВОЙСТВА ФУНКЦИЙ
- •Задачи для самостоятельного решения
- •Свойства пределов числовых последовательностей
- •Примеры
- •Свойства бесконечно малых последовательностей
- •Задачи для самостоятельного решения
- •Свойства предела функции
- •Примеры решения задач
- •Раскрытие неопределенностей
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Рекомендованная литература
- •Задачи для индивидуального выполнения
- •Правила дифференцирования
- •Производные основных элементарных функций
- •Логарифмическая функция
- •Показательная функция
- •Обратные тригонометрические функции
- •Производная функции, заданной параметрически
- •Логарифмическое дифференцирование
- •Производные высших порядков
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Связь между монотонностью функции и ее производной
- •Наибольшее и наименьшее значение функции
- •Задачи для самостоятельного решения
- •Свойства неопределенного интеграла
- •Свойства определенного интеграла
- •Непосредственное интегрирование
- •Метод интегрирования по частям
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •ДУХОН Михаил Юльевич
- •Часть 2
|
lim |
f (x)= lim |
|
8 |
|
|
= |
|
|
|
8 |
|
|
|
= |
|
|
8 |
|
|
|
|
= +∞. |
||||||||
|
16 − x2 |
16 −(−4 +0)2 |
|
16 −16 +8 0 −02 |
|
||||||||||||||||||||||||||
|
x→−4−0 |
x→−4+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
lim |
f (x)= lim |
8 |
|
|
= |
|
8 |
|
|
= |
|
|
|
|
|
|
8 |
|
|
= +∞. |
||||||||||
16 − x2 |
|
16 −(4 −0)2 |
|
|
16 −16 + 8 0 − |
02 |
|
||||||||||||||||||||||||
|
x→−4−0 |
x→4−0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
lim |
f (x)= lim |
|
8 |
|
|
|
= |
|
|
8 |
|
|
|
|
|
= |
8 |
|
|
|
|
|
= −∞. |
|||||||
|
|
|
|
|
|
|
16 −(4 +0)2 |
16 −16 −8 0 − |
02 |
||||||||||||||||||||||
|
x→−4−0 |
x→4+0 16 − x2 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
График функции имеет две вертикальных асимптоты, уравне- |
|||||||||||||||||||||||||||||
ния которых x = −4 и x = 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Найдем пределы функции при x → −∞ и при x → +∞ |
|
|
|
|
|||||||||||||||||||||||||
|
|
lim f |
(x) |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
= 0. |
|
|
|
|
|
|
|||||||
|
|
= lim |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
16 − x |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
x→−∞ |
|
|
|
|
|
|
|
x→−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
lim f |
(x) |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
= 0. |
|
|
|
|
|
|
|||||||
|
|
= lim |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
16 − x |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
x→+∞ |
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
График функции имеет горизонтальную асимптоту, уравне- |
|||||||||||||||||||||||||||||
ние которой y = 0 (ось абсцисс). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Поскольку |
|
пределы |
|
функции f (x) |
при x → −∞ и при |
||||||||||||||||||||||||
|
x → +∞ равны нулю, |
тем |
|
|
более |
|
равны |
нулю пределы |
функции |
||||||||||||||||||||||
|
f (x) |
при x → −∞ и при |
|
|
x → +∞, а следовательно, наклонных |
||||||||||||||||||||||||||
|
x |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
асимптот у функции нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
7) Построим график функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Наибольшее и наименьшее значение функции |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
Теорема 2.16. Пусть функция f (x) |
|
|
непрерывна на отрезке |
||||||||||||||||||||||||||
[a;b]. Тогда она достигает на этом отрезке своего наименьшего и наибольшего значения.
127
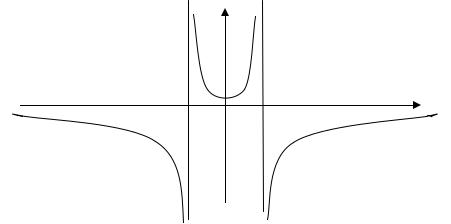
у
-4 |
4 |
х |
|
О |
|
|
|
Рис. 2.3.16
128
Для того чтобы найти наибольшее или наименьшее значение функции, непрерывной в некотором промежутке, следует вычислить значения функции на концах промежутка и во всех критических точках, принадлежащих этому промежутку. Наименьшее и наибольшее из полученных значений являются соответственно наименьшим и наибольшим значениями функции в рассматриваемом промежутке.
Можно предложить следующий алгоритм отыскания наименьшего и наибольшего значений функции на отрезке.
Для того, чтобы найти наибольшее и наименьшее значение функции f (x) на отрезке [a;b], нужно:
1) Найти область определения функции f (x) и убедиться в ее непрерывности на этом отрезке.
2) Найти производную функции f (x).
3) Приравнять производную к нулю и решить полученное уравнение. Корни этого уравнения, а также точки, в которых производная не существует (но существует функция), являются критическими точками функции. Отобрать из числа критических точек те,
которые лежат на отрезке [a;b].
4) Вычислить значение функции в отобранных критических точках, а также на концах отрезка – в точках а и b. Наименьшее и наибольшее из числа вычисленных значений и являются наименьшим
и наибольшим значениями функции на отрезке [a;b].
Пример 2.3.16. Найти наибольшее и наименьшее значения функции f (x)= x2 − 2 x + 2 на отрезке [−1; 2].
Решение. Областью определения функции f (x) является
множество всех действительных чисел. Функция непрерывна на заданном отрезке.
Найдем производную функции.
f ′(x)= (x2 − 2 x + 2)′ = 2 x − 2.
Приравняем производную к нулю и решим полученное урав-
нение.
129
2 x − 2 = 0 x = 1.
Критическая точка x = 1 принадлежит отрезку [−1; 2].
Вычислим значение функции на концах отрезка – в точках x = −1 и x = 2 , а также в критической точке x = 1 .
f (−1)= (−1)2 − 2 (−1)+ 2 = 5. f (2)= 22 − 2 2 + 2 = 2.
f (1)= 12 − 2 1 + 2 = 1.
Наибольшее значение функция принимает в точке x = −1 . Это значение равно 5.
Наименьшее значение функция принимает в точке x = 1 . Это значение равно 1.
Пример 2.3.17. Найти наибольшее и наименьшее значения функции
f (x)= x3 + 3x2 + 3
на отрезке [−1;1].
Решение. Областью определения функции f (x) является
множество всех действительных чисел. Функция непрерывна на заданном отрезке.
Найдем производную функции.
f ′(x)= (x3 + 3x2 + 3)′ = 3x2 +6 x.
Приравняем производную к нулю и решим полученное урав-
нение.
3x2 +6 x = 0.
Корнями этого уравнения являются числа x1 = 0 и x2 = −2 . Второй из этих корней не входит в заданный отрезок. В заданном отрезке содержится только одна критическая точка x1 = 0 . Вычислим значение функции в конечных точках интервала и в критической точке x1 = 0 .
130
f (−1)= (−1)3 + 3(−1)2 + 3 = −1 + 3 + 3 = 5. f (1)= 13 + 3 12 + 3 = 1 + 3 + 3 =7.
f (0)= 03 + 3 02 + 3 = 3.
Наибольшее значение функция принимает в точке x = 1 . Это значение равно 7.
Наименьшее значение функция принимает в точке x = 0 . Это значение равно 3.
Пример 2.3.18. Найти наибольшее и наименьшее значения функции
f (x)= 25 − x2 .
на отрезке [−4;4].
Решение. Областью определения функции f (x) является множество [−5;5]. Функция непрерывна на заданном отрезке.
Найдем производную функции.
f ′(x)= ( 25 − x2 )′ = − |
x |
|
. |
25 − x |
2 |
||
|
|
|
Приравняем производную к нулю и решим полученное урав-
нение.
− |
x |
= 0 x = 0. |
25 − x2 |
Корнем этого уравнения является число x = 0 . Этот корень входит в заданный отрезок. В заданном отрезке содержится критическая точка x = 0 . Вычислим значение функции в конечных точках интервала и в критической точке x = 0 .
f (−4)= 25 −(−4)2 = 3.
f (4)= 25 −(4)2 = 3.
131

f (0)= 25 −(0)2 = 5.
Наименьшее значение функция принимает в точках x = −4 и x = 4 . Это значение равно 3.
Наибольшее значение функция принимает в точке x = 0 . Это значение равно 5.
Задачи на отыскание наименьших и наибольших значений функции. Задачи на отыскание наибольших и наименьших значений представляют собой применение рассмотренных выше инструментов исследования функций к решению задач с практическим содержанием. Решение этих задач предполагает формализацию условий задачи
– построение функции и исследование этой функции при помощи производной. Для решения задач этого типа можно предложить следующий алгоритм:
1.На первом этапе следует построить функцию, отражающую условия задачи. Для
этого нужно:
а) Выбрать величину, которая будет играть роль функции; в качестве функции
следует выбирать величину, которая по условиям задачи должна принять
наибольшее или наименьшее значение.
б) Выбрать величину, которая будет играть роль аргумента; в этом качестве
следует выбрать одну из величин, от которых зависит функция; желательно
выбрать ту из них, через которую функция выражается проще
всего.
в) Выразить функцию через аргумент.
г) Найти область определения функции, причем область определения зависит не
только от вида функции, но и от содержательных условий за-
дачи.
2.На втором этапе следует исследовать функцию при помощи производной.
132

Пример 2.3.19. Число 18 разбить на такие два слагаемые, чтобы сумма их квадратов была наименьшей.
Решение. В качестве функции (обозначим ее через у) будем рассматривать сумму квадратов слагаемых. В качестве аргумента (обозначим через х) примем первое слагаемое. Тогда второе слагаемое равно 18 − x . Тогда по условиям задачи
y = x2 +(18 − x)2 .
Областью определения функции является множество всех действительных чисел.
Найдем производную функции:
y′ = (x2 +(18 − x)2 )′ = (x2 + 324 − 36 x + x2 )′ = (2x2 − 36 x + 324)′ = 4 x − 36.
Приравняем производную к нулю и решим полученное уравнение.
4 x − 36 = 0 x = 9.
Для исследования критической точки найдем вторую производную.
y′′ = (4 x − 36 )′ = 4 > 0.
Вторая производная положительна независимо от аргумента и, следовательно, в критической точке. Таким образом, в силу второго достаточного условия экстремума точка x = 9 является точкой минимума функции. Таким образом, сумма квадратов является наименьшей, если первое слагаемое равно 9, а следовательно, второе слагаемое также равно 9.
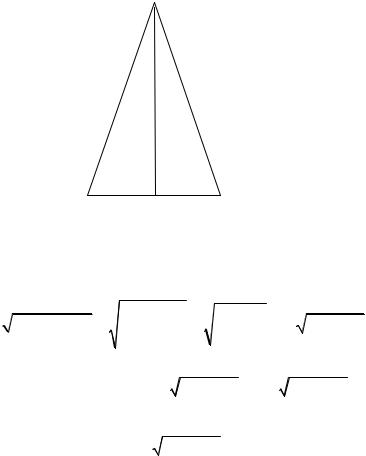
Пример 2.3.20. Среди равнобедренных треугольников с боковой стороной, равной 8, найти треугольник наибольшей площади.
Решение. Рассмотрим равнобедренный треугольник АВС (рис. 2.3.17), у которого АВ = ВС = 8. В качестве функции выберем площадь треугольника (обозначим ее у).
Выберем в качестве аргумента основание АС (обозначим его x ). Проведем высоту ВН. Поскольку эта высота является также и
медианой, AH = 21 AC = 2x .
133
В
8 |
8 |
А |
Н х |
С |
Рис. 2.3.17
Рассмотрим треугольник АВН. По теореме Пифагора
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
x |
2 |
|
x2 |
|
|
1 |
|
|
2 |
. |
|||||
BH = |
AB |
|
− AH |
|
= |
8 |
|
|
− |
|
|
|
|
= 64 − |
|
|
|
|
= |
|
256 |
− x |
|
||||
|
|
|
|
|
|
|
|
|
4 |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
Площадь треугольника АВС равна |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
S ABC |
= |
1 |
AC BH = |
1 |
|
x |
1 |
|
|
256 − x2 |
= |
|
1 |
x |
256 − x2 . |
|
|
||||||||||
|
2 |
|
2 |
|
|
|
|
|
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||||||
Функция имеет вид: |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
y = |
|
x |
|
256 − x2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем область определения функции. Очевидно, что АС > 0, а из неравенства треугольника следует: AC < AB + BC = 8 + 8 = 16.
Таким образом, область определения функции имеет вид: x (0;16 ).
Теперь займемся исследованием функции. Найдем ее производную.
134
y′ = |
|
1 |
x |
256 − x |
2 |
′ |
= |
|
1 |
256 |
− x |
2 |
+ |
1 |
x ( |
|
256 − x |
2 |
) |
′ |
= |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
4 |
|
4 |
|
4 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
x |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
x2 |
|||||
= |
|
|
256 |
− x |
|
+ |
|
|
|
x |
− |
|
|
|
|
|
|
|
|
= |
|
|
|
256 |
− x |
|
− |
|
|
|
|
|
= |
|||||||
4 |
|
|
4 |
|
|
|
|
256 − x2 |
4 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
256 − x2 |
||||||||||||||
|
256 |
|
− x |
2 − x2 |
|
|
|
256 − |
2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
|
|
|
|
|
|
− x2 |
|
|
= |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
|
256 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
256 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
нение. |
|
Приравняем производную к нулю и решим полученное урав- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
256 − 2 x |
|
|
= 0 |
|
256 − 2 x |
= 0, |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
4 |
|
256 |
− x |
2 |
|
|
|
256 − x2 > 0. |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Корнями этого уравнения являются числа x1,2 = ±8 2 . Ко-
рень x = −8 2 не входит в область определения функции. Критиче-
скую точку x = 8 2 исследуем при помощи первого достаточного условия экстремума. Разобьем область определения функции на интервалы в этой точке (рис. 2.3.18).
Рис. 2.3.18
Найдем знак производной на каждом из интервалов области определения.
y′(8)= 256 − 2 82 |
= |
128 |
> 0. |
|
4 192 |
||||
4 256 −82 |
|
|
135
y′(12)= 256 − 2 122 |
= − |
32 |
< 0. |
|
4 112 |
||||
4 256 −122 |
|
|
||
Таким образом, в точке x = 8 |
2 |
производная меняет знак с |
||
“плюс” на “минус” и следовательно, в точке x = 8 |
2 функция имеет |
|||
максимум. Треугольник имеет набольшую площадь, если его основа-
ние равно 8 2 . Несложно убедиться, что треугольник АВС удовлетворяет условиям теоремы Пифагора, а следовательно является прямоугольным.
В качестве аргумента можно было выбрать и другую величину. Пусть в качестве аргумента будет выбран угол АВС. Обозначим его β . Выразим площадь треугольника АВС через этот аргумент.
S ABC = 21 AB BC sin ABC = 21 8 8 sin β = 32 sin β .
Функция имеет вид:
y = 32 sin β .
Областью определения функции является интервал (0;π ). Найдем производную функции
y′ = (32 sin β )′ = 32 cos β .
Приравняем производную к нулю и решим полученное урав-
нение.
32 cos β = 0 cos β = 0 β = π2 +πn, n Z.
Очевидно, единственным решением уравнения, принадлежа-
щим области определения, является β = π2 . Для того, чтобы иссле-
довать эту критическую точку, найдем вторую производную. y′′ = (32 cos β )′ = −32 sin β .
В исследуемой критической точке вторая производная равна: y′′ π2 = −32 sin π2 = −32 < 0.
136
