
- •М.Ю. ДУХОН
- •Часть 2
- •МОСКВА – 2005
- •СВОЙСТВА ФУНКЦИЙ
- •Задачи для самостоятельного решения
- •Свойства пределов числовых последовательностей
- •Примеры
- •Свойства бесконечно малых последовательностей
- •Задачи для самостоятельного решения
- •Свойства предела функции
- •Примеры решения задач
- •Раскрытие неопределенностей
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Рекомендованная литература
- •Задачи для индивидуального выполнения
- •Правила дифференцирования
- •Производные основных элементарных функций
- •Логарифмическая функция
- •Показательная функция
- •Обратные тригонометрические функции
- •Производная функции, заданной параметрически
- •Логарифмическое дифференцирование
- •Производные высших порядков
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Связь между монотонностью функции и ее производной
- •Наибольшее и наименьшее значение функции
- •Задачи для самостоятельного решения
- •Свойства неопределенного интеграла
- •Свойства определенного интеграла
- •Непосредственное интегрирование
- •Метод интегрирования по частям
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •ДУХОН Михаил Юльевич
- •Часть 2
2.3. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
Связь между монотонностью функции и ее производной
Теорема 2.9. Пусть функция f (x) дифференцируема на не-
котором промежутке. Тогда для того, чтобы функция f (x) возрас-
тала (убывала) на этом промежутке, необходимо и достаточно, чтобы в каждой точке этого промежутка ее производная была положительна (отрицательна).
Соответственно, для того чтобы функция была неубывающей (невозрастающей) на некотором промежутке, необходимо и достаточно, чтобы в каждой точке этого промежутка ее производная была неотрицательна (неположительна).
Пример 2.3.1. Исследовать на монотонность функцию f (x)= x2 −6 x + 5.
Решение. Найдем производную функции f (x). f ′(x)= (x2 −6 x + 5)′ = 2 x −6.
Приравняем производную к нулю и решим полученное урав-
нение.
2 x −6 = 0 x = 3.
Разобьем в точке x = 3 область определения функции (в данном примере – это множество всех действительных чисел) на интер-
валы (рис.2.3.1.).
Рис. 2.3.1
102

Вычислив значение производной в одной из внутренних точек каждого интервала, мы определим знак производной на каждом интервале. Например,
f ′(0)= 2 0 −6 = −6 < 0 , f ′(5)= 2 5 −6 = 4 > 0 .
В соответствии с теоремой 2.3.1. на интервале (−∞; 3) функ-
ция убывает; на интервале (3;+∞) функция возрастает.
Пример 2.3.2. Исследовать на монотонность функцию
|
f (x)= |
|
1 |
x3 − 4 x2 |
+ 15 x + 2. |
||||||||
|
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
f (x). |
||
Решение. Найдем производную функции |
|
||||||||||||
|
1 |
|
3 |
|
|
|
|
2 |
|
′ |
2 |
|
|
f ′(x)= |
|
|
x |
|
− |
4 x |
|
+ 15 x + 2 = x |
|
−8 x + 15. |
|||
3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Приравняем производную к нулю и решим полученное урав-
нение.
x2 −8 x + 15 = 0.
Корнями этого уравнения являются числа x1 = 3 и x2 = 5. Разобьем в точках x1 = 3 и x2 = 5 область определения
функции (в данном примере – это множество всех действительных чисел) на интервалы (рис.2.3.2).
Вычислив значения производной во внутренних точках каждого интервала, определим знак производной на каждом интервале.
f ′(0)= 02 −8 0 + 15 = 15 > 0. f ′(4)= 42 −8 4 + 15 = −1 < 0.
Рис. 2.3.2
103
f ′(6 )= 62 −8 6 + 15 = 3 > 0.
Следовательно, в силу теоремы 2.3.1 функция возрастает на множестве (−∞; 3)U (5;+∞); функция убывает на множестве
(3;5).
Экстремумы функции. Точка x0 называется точкой локаль-
ного максимума (минимума) функции f (x), если в некоторой окре-
стности этой точки (т. е. на интервале (x −ε , x +ε ), где ε > 0 ) зна-
чение функции в этой точке f (x0 ) является наибольшим (наимень-
шим). Точки локального максимума и минимума функции называют-
ся точками экстремума.
Теорема 2.10. (необходимое условие экстремума). Пусть функция f (x) непрерывна в некоторой окрестности точки x0 . Для
того, чтобы в точке x0 функция f (x) имела локальный экстремум
(максимум или минимум), необходимо, чтобы производная функции в этой точке равнялась нулю.
Точка, в которой производная функции равна нулю (или не существует), называется критической точкой функции. В критической точке функция может иметь максимум, может иметь минимум, но может не иметь ни того ни другого, т. е. в этой точке экстремума может и не быть. Для того, чтобы исследовать характер критической точки, используются достаточные условия экстремума.
Теорема 2.11. (первое достаточное условие экстремума). Пусть x0 – критическая точка функции f (x). Тогда возможны три
случая:
1) Если в некоторой окрестности точки x0 слева от нее производная f ′(x) положительна, а справа – отрицательна, то в точке x0 функция имеет максимум.
104

2) |
Если в некоторой окрестности точки x0 слева от нее про- |
||
изводная |
f ′(x) отрицательна, а справа – положительна, то в точке |
||
x0 функция имеет минимум. |
|||
3) |
Если в некоторой окрестности точки x0 слева и справа от |
||
нее производная f ′(x) |
имеет одинаковый знак, то функция f (x) в |
||
точке x0 |
экстремума не имеет. |
||
Теорема 2.12. (второе достаточное условие экстремума). |
|||
Пусть x0 |
– критическая точка функции f (x). Тогда возможны три |
||
случая: |
|
x0 |
вторая производная функции f (x) отри- |
1) |
Если в точке |
||
цательна ( f ′′(x)< 0 ), |
то в точке x0 функция имеет максимум. |
||
2) |
Если в точке |
x0 |
вторая производная функции f (x) по- |
ложительна ( f ′′(x)> 0 ), |
то в точке x0 функция имеет минимум. |
||
3) |
Если в точке x0 |
вторая производная функции f (x) равна |
|
нулю ( f ′′(x)= 0 ), то функция f (x) в точке x0 экстремума не
имеет.
Второе достаточное условие экстремума не может быть использовано в тех случаях, когда первая производная в критической точке не существует.
Пример 2.3.3. Исследовать функцию
f (x)= 31 x3 − 3x2 + 8 x −1
на монотонность и экстремумы.
Решение. Найдем производную функции f (x).
|
1 |
|
3 |
|
2 |
|
′ |
2 |
|
|
f ′ (x)= |
|
x |
|
− 3x |
|
+ 8 x −1 |
|
= x |
|
−6 x + 8. |
3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
105
Приравняем производную к нулю и решим полученное урав-
нение:
x2 −6 x + 8 = 0.
Корнями этого уравнения, а следовательно и критическими точками функции f (x) являются числа x1 = 2 и x2 = 4.
Разобьем область определения функции (т. е. множество всех действительных чисел) в точках x1 = 2 и x2 = 4 на интервалы (рис. 2.3.3).
Рис. 2.3.3 |
|
Таким образом, |
функция f (x) возрастает на множестве |
(−∞; 2)U (4;+∞) и убывает на множестве (2;4). |
|
В точке x1 = 2 |
производная меняет свой знак с “плюс” на |
“минус” и, следовательно, в соответствии с теоремой 2.11, это точка максимума. Найдем значение функции в точке
f(2)= 31 23 − 3 22 + 8 2 −1 = 83 −12 + 16 −1 = 5 23 .
Вточке x2 = 4 производная меняет свой знак с “минус” на
“плюс” и, следовательно, в соответствии с теоремой 2.11, это точка минимума. Найдем значение функции в точке x2 = 4 .
f (4)= 31 43 − 3 42 + 8 4 −1 = 643 − 48 + 32 −1 = 4 13 .
106
|
|
|
|
|
|
2 |
|
|
Таким образом, |
в точке A |
2;5 |
|
функция |
||||
3 |
||||||||
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
мум, в точке B |
4;4 |
|
|
функция имеет минимум. |
||||
3 |
||||||||
|
|
|
|
|
|
|
||
Можно |
предложить следующий |
алгоритм |
||||||
функции на монотонность и экстремумы.
имеет макси-
исследования
1)Найти область определения функции.
2)Найти производную функции.
3)Приравнять производную к нулю решить полученное уравнение. Корни этого уравнения, а также точки, в которых производная не существует (если они входят в область определения функции), являются критическими точками функции.
4)Разбить область определения на интервалы в критических точках функции.
5)Определить знак производной на каждом из полученных интервалов.
6)Интервалы, на которых производная положительна, являются интервалами возрастания, а интервалы, на которых производная отрицательна, являются интервалами убывания. Критические точки, в которых производная меняет знак с “плюс” на “минус”, являются точками максимума; точки, в которых производная меняет знак с “минус” на “плюс”, являются точками минимума; точки, в которых производная не меняет знак, не являются точками экстремума.
Пример 2.3.4. Исследовать функцию f (x)= (x − 3) x .
на монотонность и экстремумы.
Решение.
1)Областью определения функции f (x) является множест-
во [0;+∞).
2)Найдем производную функции f (x).
107
f ′ (x)= ((x − 3) x )′ = (x − 3)′ x +(x − 3) ( x )′ =
= |
x + |
|
x − 3 |
= |
2 x + x − 3 |
|
= |
3x − 3 |
= |
3(x −1) |
. |
||
|
2 x |
|
|
|
|||||||||
|
|
|
|
|
2 x |
|
2 x |
|
2 x |
||||
3) Приравняем производную к нулю и решим полученное |
|||||||||||||
уравнение. |
|
|
|
|
(x −1)= 0, |
|
|
||||||
|
|
|
3(x −1) |
|
|
|
|||||||
|
|
|
3 |
|
|
||||||||
|
|
|
|
= 0 |
|
|
|
|
x = 1. |
||||
|
2 |
x |
x ≠ 0; |
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, критическими точками функции являются точки x = 1 , а также точка x = 0 , в которой производная не существует.
4) Разобьем область определения функции f (x) на интервалы в точках x = 0 и x = 1 (рис. 2.3.4).
Рис. 2.3.4
5) Определим знак производной на каждом из полученных интервалов.
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
1 |
|
|
3 |
|
|
|
− |
1 |
|
|
3 |
|
||||
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
||||||||
f ′ |
|
|
|
= |
|
|
|
= − |
|
< 0. |
|||||||
|
|
|
|
|
|
|
1 |
|
2 2 |
||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
′ |
|
|
|
|
3(4 −1) |
|
9 |
|
||||||
|
f |
(4)= 2 4 = 4 > 0. |
|||||||||||||||
|
|
|
|||||||||||||||
108
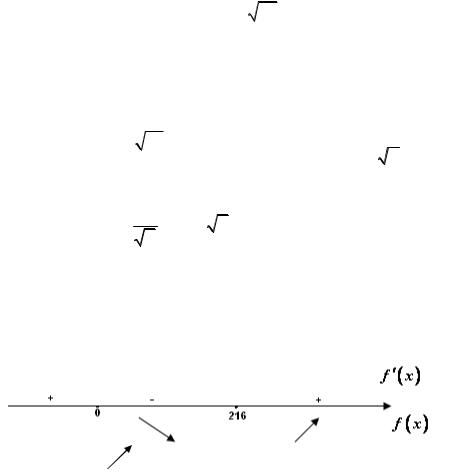
6) Функция f (x) возрастает на множестве (1;+∞), убыва-
ет на множестве (0;1), в точке M (1;−2) функция имеет минимум.
Пример 2.3.5. Исследовать функцию f (x)= x −6 3 x2 .
на монотонность и экстремумы.
Решение.
1)Областью определения функции является множество всех действительных чисел.
2)Найдем производную функции.
f ′ (x)= |
( |
3 |
2 |
) |
′ |
|
2 |
′ |
|
− |
1 |
|
|
6 |
|
|
|
|
|
|
|
||||||||||
x −6 x |
|
|
|
|
|
= 1 −6 x |
3 |
= 1 − |
|
|
. |
||||
|
|
|
3 |
x |
|||||||||||
|
|
|
|
= x −6 x 3 |
|
|
|
||||||||
3) Приравняем производную к нулю и решим полученное уравнение.
1 − 36x = 0 3 x = 6 x = 216.
Критическими точками функции являются точки x = 0, в ко-
торой производная не существует (но существует сама функция) и точка x = 216.
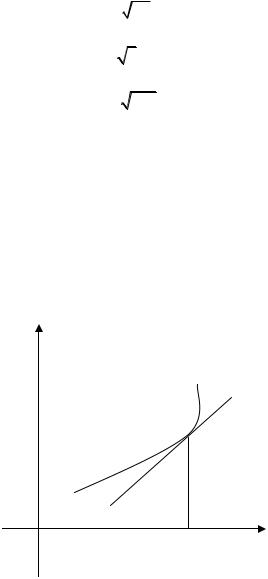
4) Разобьем область определения функции (т. е. множество всех действительных чисел) на интервалы в точках x = 0 и x = 216
(рис. 2.3.5).
Рис. 2.3.5
5) Определим знак производной функции на каждом из интер-
валов.
109
|
|
′ |
(−1)= 1 |
|
|
|
6 |
|
|
|
|
||
|
f |
− 3 |
−1 =7 > 0. |
|
|||||||||
|
|
|
|||||||||||
|
|
|
′ |
|
|
6 |
|
|
|
|
|
|
|
|
|
f |
(1)= 1 − 3 1 = −5 < 0. |
|
|||||||||
|
|
|
|
||||||||||
|
′ |
(343)= 1 |
|
|
|
6 |
|
|
1 |
|
|||
f |
− 3 |
343 = 7 > 0. |
|
||||||||||
|
|
||||||||||||
6) Таким образом, функция |
f (x) |
возрастает на множестве |
|||||||||||
(−∞;0)U (216;+∞), убывает на |
|
множестве (0; 216 ), в точке |
|||||||||||
M (0;0) функция имеет максимум, в точке N (216;0) |
функция |
||||||||||||
имеет минимум. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Направления выпуклости функции. Точки перегиба. Если |
|||||||||||||
в некоторой окрестности точки |
x0 график функции f (x) |
располо- |
|||||||||||
жен не ниже (не выше) касательной к графику этой функции в точке x0 , то говорят, что график функции f (x) в точке x0 имеет выпук-
лость вниз (вверх).
у
О |
x0 |
х |
Рис. 2.3.6
110
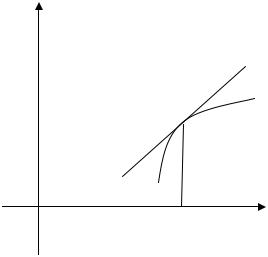
у
О |
x0 |
х |
Рис. 2.3.7 |
|
|
Точка |
x0 называется точкой перегиба функции f (x), если |
|
существует окрестность точки x0 такая, что в этой окрестности слева от x0 (т. е. при x < x0 ) и справа от этой точки (т. е. при x > x0 ) функция f (x) имеет разное направление выпуклости.
Для определения направления выпуклости графика функции можно воспользоваться следующей теоремой.
Теорема 2.13. Пусть функция f (x) определена и непрерывна на некотором интервале. Если в каждой точке этого интервала вторая производная функции f (x) неотрицательна (неположительна), то график функции на этом интервале имеет выпуклость вниз (вверх).
Теорема 2.14 (необходимое условие точки перегиба). Пусть график функции f (x) имеет точку перегиба x0 , причем существует
111
непрерывная производная второго порядка f ′′(x) в некоторой окрестности точки x0 . Тогда f ′′(x)= 0.
Теорема 2.15 (достаточное условие точки перегиба). Пусть |
||
f ′′(x0 )= 0 или f ′′(x0 ) |
не существует. Если f ′′(x) |
меняет знак |
при переходе через точку |
x0 , то в этой точке график функции имеет |
|
перегиб. |
|
|
Пример 2.3.6. Исследовать на выпуклость (вогнутость) функ- |
||
цию |
|
|
f (x)= x3 −6 x2 + 2 x −1. |
|
|
Решение. Найдем вторую производную функции |
f (x). |
|
f ′(x)= (x3 −6 x2 + 2 x −1)′ = 3x2 −12 x + 2.
f ′′(x)= (3x2 −12 x + 2)′ = 6 x −12.
Приравняем вторую производную к нулю и решим полученное уравнение.
6 x −12 = 0 x = 2.
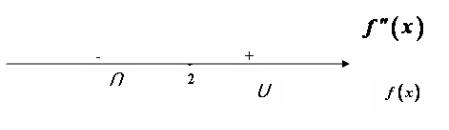
График функции имеет единственную точку перегиба x0 = 2. Разобьем область определения функции, т. е. множество всех действительных чисел на интервалы в точке x0 (рис. 2.3.8).
Рис. 2.3.8
112

Определим знак второй производной функции f (x) на каж-
дом из интервалов.
f ′′(0)= 6 0 −12 = −12 < 0. f ′′(3)= 6 3 −12 = 6 > 0.
Таким образом, график функции является выпуклым вверх на множестве (−∞; 2) и выпуклым вниз на множестве (2;+∞). Точка
P (2;−1) является точкой перегиба функции f (x).
Пример 2.3.7. Исследовать на выпуклость (вогнутость) функ-
цию
f (x)= x3 x+ 8 .
Решение. Областью определения функции f (x) является
множество (−∞;0)U (0;+∞). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдем вторую производную функции |
f (x). |
|
|
|||||||||||||
x3 |
+ 8 |
′ |
|
|
2 |
|
8 |
′ |
|
|
8 |
|
||||
f ′ (x)= |
|
|
= |
x |
|
|
+ |
|
= 2x − |
|
|
. |
||||
|
x |
|
|
|
x |
2 |
||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|||||
f ′′(x) |
|
|
8 |
|
|
′ |
|
|
16 |
|
|
|
||||
= |
2 x − |
|
|
|
|
|
= 2 + |
|
3 . |
|
|
|
||||
|
x |
2 |
|
|
x |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Приравняем вторую производную к нулю и решим полученное уравнение.
2 + 16x3 = 0 x3 = −8 x = −2.
Таким образом, точкой перегиба функции f (x) является точка P (−2;0).
Разобьем область определения функции на интервалы в точке x0 = −2 (рис. 2.3.9).
113
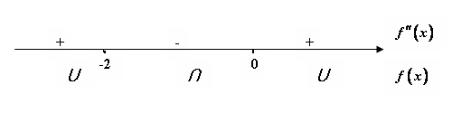
Рис. 2.3.9
Определим знак второй производной на каждом интервале.
f ′′(−4)= 2 + |
16 |
|
|
= 2 − |
1 |
= 7 > 0. |
|||||
(−4)3 |
4 |
||||||||||
|
|
|
|
|
4 |
||||||
f ′′(−1) |
= 2 + |
|
|
16 |
|
|
= 2 −16 = −14 < 0. |
||||
(−1)3 |
|
||||||||||
|
|
|
|
|
|
|
|||||
f ′′(1)= 2 + |
|
16 |
|
= 2 + 16 = 18 > 0. |
|||||||
(1)3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
Таким образом, график функции имеет выпуклость вверх на |
|||||||||||
множестве (−2;0) |
и |
|
|
выпуклость |
|
вниз на множестве |
|||||
(−∞;−2)U (0;+∞). Точкой перегиба является точка P (−2;0).
Асимптоты функции. Если график функции как угодно близко приближается к некоторой прямой, то такая прямая называет-
ся асимптотой функции.
Существует три вида асимптот: вертикальные, горизонтальные и наклонные.
1. Вертикальные асимптоты. Для того чтобы составить уравнения вертикальных асимптот функции f (x) (или убедиться в
их отсутствии), нужно:
а) Выявить точки, в которых возможно существование вертикальной асимптоты. К таким точкам относятся изолированные точки разрыва и крайние точки открытых интервалов области определения.
114

б) Пусть такой точкой является точка x0 . Исследовать пове-
дение функции в каждой из выявленных точек. Для этого нужно найти оба односторонних предела функции в этой точке. Если хотя бы
один из односторонних пределов в точке x0 бесконечен, то функция имеет вертикальную асимптоту, уравнение которой x = x0 .
Пример 2.3.8. Исследовать на наличие вертикальных асимптот функцию
f (x)= x2x+ 1 .
Решение. Функция f (x) имеет единственную точку разрыва x0 = 0. Исследуем поведение функции f (x) в окрестности точки x0 . Найдем односторонние пределы в этой точке.
lim f (x)= |
|
x2 |
+ 1 |
|
|
|
1 |
|
|
|
lim |
|
|
|
= lim |
x + |
|
|
|
= −∞. |
|
|
x |
x |
||||||||
x→0−0 |
x→0−0 |
|
|
x→0−0 |
|
|
|
|
||
lim f (x)= |
|
x2 |
+ 1 |
|
|
|
1 |
|
|
|
lim |
|
|
|
= lim |
x + |
|
|
|
= +∞. |
|
|
x |
|
|
|
||||||
x→0+0 |
x→0+0 |
|
|
x→0+0 |
|
x |
|
|||
Функция f (x) |
имеет вертикальную асимптоту, уравнение |
|||||||||
которой x = 0 (ось ординат).
Пример 2.3.9. Исследовать на наличие вертикальных асимптот функцию
f (x)= ln x.
Решение. Областью определения функции f (x) является от-
крытый интервал (0;+∞). Крайней точкой этого интервала является точка x = 0. Найдем правый предел функции f (x) в этой точке
(левый предел, очевидно, отсутствует).
lim ln x = −∞.
x→0+0
115
Функция f (x) имеет вертикальную асимптоту, уравнение которой x = 0 (ось абсцисс).
2. Горизонтальные асимптоты. Для того чтобы составить уравнения вертикальных асимптот функции f (x) (или убедиться в их отсутствии), нужно:
а) Найти предел функции при x → −∞. Если этот
предел существует, конечен и равен числу b, то функция имеет горизонтальную асимптоту, уравнение которой
б) Провести аналогичное исследование при
Пример 2.3.10. Исследовать на наличие горизонтальных асимптот функцию
f(x)= 2 x2 −1 .
x2 + 1
Решение. Найдем пределы функции при x → −∞ и при x → +∞.
lim |
f (x)= lim |
2 x2 |
−1 |
= 2. |
x→−∞ |
x→−∞ |
x2 |
+ 1 |
|
lim |
f (x)= lim |
2 x2 |
−1 |
= 2. |
x→+∞ |
x→+∞ |
x2 |
+ 1 |
|
Функция f (x) имеет единственную горизонтальную асимптоту (как слева, так и справа), уравнение которой
Пример 2.3.11. Исследовать на наличие горизонтальных асимптот функцию
f (x)= arctgx.
Решение. Найдем пределы функции при x → −∞ и при x → +∞.
lim |
f (x)= lim arctgx = − |
π . |
x→−∞ |
x→−∞ |
2 |
116

lim |
f (x)= lim arctgx = |
π . |
x→+∞ |
x→+∞ |
2 |
Функция f (x) |
имеет две горизонтальные асимптоты, урав- |
|
нения которых
y = −π2 (слева) и y = π2 (справа).
3. Наклонные асимптоты. Для того, чтобы составить уравнения наклонных асимптот функции f (x) (или убедиться в их отсутствии), нужно:
а) Найти предел функции f (xx) при x → −∞. Если этот
предел существует, конечен и равен числу k ≠ 0 , то следует найти еще один предел:
lim ( f (x)− kx).
x→−∞
Если и этот предел существует, конечен и равен числу b , то функция f (x) имеет наклонную асимптоту, уравнение которой y = kx + b.
б) Провести аналогичное исследование при x → +∞.
Пример 2.3.12. Исследовать на наличие наклонных асимптот
функцию f (x)= |
3x2 + 1 |
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
x − 2 |
|
|
f (x) |
|
|
|||||
Решение. Найдем предел функции |
|
при x → −∞. |
||||||||||
|
|
|
||||||||||
|
f (x) |
|
|
|
|
|
|
x |
|
|||
lim |
= |
lim |
3x2 + 1 |
= |
lim |
3x2 + 1 |
= 3. |
|||||
|
|
|
||||||||||
x→−∞ |
x |
x→−∞ x (x − 2) |
|
x→−∞ x2 − 2 x |
|
|||||||
Итак, k = 3. Найдем еще один предел:
117

|
( f (x)− kx)= |
|
3x |
2 |
+ 1 |
|
|
|
3x |
2 |
+ 1 − 3x |
2 |
+6 x |
|
|
lim |
lim |
|
− 3x |
= |
lim |
|
|
|
= |
||||||
x − 2 |
|
|
x − 2 |
|
|
||||||||||
x→−∞ |
|
x→−∞ |
|
|
x→−∞ |
|
|
|
|
|
|
||||
= xlim→−∞ 6xx−+21 = 6.
|
Слева (т. е. при |
x → −∞) функция имеет наклонную асим- |
|||||||||||||||||||
птоту, уравнение которой |
y = 3x +6. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Найдем предел функции |
|
f (x) |
|
при x → +∞. |
|
|
|
|
|
|||||||||||
|
|
x |
|
|
|
|
|
|
|||||||||||||
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
= |
lim |
|
|
3x2 + 1 |
= lim |
3x2 + 1 |
= 3. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x→+∞ |
x |
x→+∞ x (x − 2) |
|
x→+∞ x2 − 2 x |
|
|
|
|
|
|||||||||||
|
Итак, k = 3. Найдем еще один предел: |
|
|
|
|
|
|
|
|
||||||||||||
|
( f (x)− kx)= lim |
|
3x |
2 |
+ 1 |
|
|
|
|
3x |
2 |
+ |
1 − 3x |
2 |
+6 x |
|
|
||||
lim |
|
|
|
− 3x |
|
= lim |
|
|
|
= |
|||||||||||
|
|
|
|
|
|
|
x − 2 |
|
|
||||||||||||
x→+∞ |
|
x→+∞ |
x − 2 |
|
x→+∞ |
|
|
|
|
|
|
|
|||||||||
= xlim→+∞ 6xx−+21 = 6.
Справа (т. е. при x → +∞) функция имеет ту же наклонную асимптоту, уравнение которой y = 3x +6.
Пример 2.3.13. Исследовать на наличие асимптот функцию
f (x)= |
x2 |
. |
|
|
|
||
|
x2 −1 |
f (x) является |
|
Решение. Областью определения функции |
|||
множество (−∞;−1)U (1;+∞). Точками, в которых возможны вер- |
|||
тикальные асимптоты, являются точки x1 = −1 и x2 |
= 1 . Исследуем |
||
поведение функции в окрестности этих точек. |
|
||
118
lim |
f (x)= lim |
|
x2 |
|
|
= |
|
|
|
(−1 −0)2 |
|
|
|
|
= |
|
|
|
1 |
|
|
|
|
|
= +∞. |
||||||||||||||||||
|
x2 − |
1 |
|
(−1 −0)2 −1 |
|
1 + 2 0 +02 −1 |
|||||||||||||||||||||||||||||||||||||
x→−1−0 |
|
|
x→−1−0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
lim |
f (x)= lim |
|
|
x2 |
|
|
|
= |
|
|
|
(1 +0)2 |
|
= |
|
|
|
|
1 |
|
|
|
|
|
|
= +∞. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x→1+0 |
|
|
x→1+0 |
|
x2 −1 |
|
|
|
(1 +0)2 −1 |
1 + 2 |
0 +02 −1 |
|
|||||||||||||||||||||||||||||||
|
|
Функция имеет две вертикальных асимптоты, уравнения ко- |
|||||||||||||||||||||||||||||||||||||||||
торых x = −1 и x = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Найдем пределы функции при x → −∞ и при x → +∞. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
lim f |
(x)= |
lim |
|
|
x2 |
|
|
= +∞. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 − |
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
x→−∞ |
|
|
|
|
|
|
|
|
x→−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
lim f |
(x)= |
lim |
|
|
x2 |
|
|
= +∞. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 − |
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Горизонтальных асимптот функция не имеет. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
Найдем предел функции |
f (x) |
при x → −∞. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim |
|
= lim |
|
x2 |
|
|
|
|
|
|
= lim |
|
|
x |
|
|
|
|
|
= lim |
|
|
1 |
|
|
= 1. |
|||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x2 −1 |
|
|
|
1 |
|
||||||||||||||||||||||||
x→−∞ |
|
x→−∞ x x2 −1 |
|
x→−∞ |
|
|
|
|
|
x→−∞ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
k = 1. Найдем еще один предел: |
|
|
|
|
|
x2 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
( f |
(x)− kx)= |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
x2 − x x2 − |
1 |
|
||||||||||||||||||||||||
lim |
|
lim |
|
|
|
|
|
|
|
|
|
|
− x |
= |
lim |
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||
x→−∞ |
|
|
|
|
|
|
|
|
|
x→−∞ |
|
|
|
x |
−1 |
|
|
x→−∞ |
x |
−1 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 − |
1 − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= lim |
|
|
|
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x→−∞ |
1 |
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Слева (т.е. при x → −∞) функция имеет наклонную асимптоту, уравнение которой y = x.
119
|
Найдем предел функции |
|
f (x) |
при x → +∞. |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
= |
lim |
|
|
|
|
x2 |
|
|
= lim |
|
|
x |
|
= lim |
|
1 |
|
|
|
= 1. |
|
|||||||||||
x |
|
|
|
|
x2 −1 |
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||||
x→+∞ |
|
x→+∞ x |
|
x→+∞ x2 −1 x→+∞ |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
||
|
|
|
|
|
k = 1. Найдем еще один предел: |
x2 |
|
|
|
|
|||||||||||||||||||||||
|
Итак, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
( f (x)− kx)= |
|
|
x2 |
|
|
|
|
x2 |
− x x2 −1 |
|
|
|||||||||||||||||||||
lim |
lim |
|
|
|
|
|
|
|
− x = |
lim |
|
|
|
|
|
|
|
|
= |
||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
x→+∞ |
|
x |
−1 |
|
|
|
x→+∞ |
x |
−1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 − |
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= lim |
|
|
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
− 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
|
|
|
|
|
x → +∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Справа (т.е. при |
функция имеет наклонную асим- |
|||||||||||||||||||||||||||||||
птоту, уравнение которой y = x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Общая схема исследования графика функции. При иссле-
довании функции и построении ее графика рекомендуется пользоваться следующей схемой:
1.Найти область определения функции.
2.Исследовать функцию на четность и нечетность.
3.Найти точки пересечения графика с осями координат, интервалы знакопостоянства.
4.С помощью первой производной исследовать функцию на монотонность и экстремумы.
5.С помощью второй производной исследовать функцию на выпуклость и найти точки перегиба.
6.Исследовать функцию на наличие асимптот.
7.Построить график функции.
Пример 2.3.14. Исследовать функцию и построить график: f (x)= 10 − 3x − x2 .
120
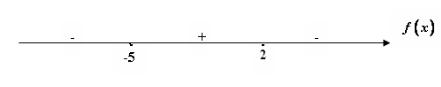
Решение.
1)Областью определения функции является множество всех действительных чисел: D ( f )= R.
2)Проверим функцию на четность:
f (−x)= 10 − 3(−x)−(−x)2 = 10 + 3x − x2 .
Функция f (x) – функция общего вида.
3) Найдем нули функции:
10 − 3x − x2 = 0 x2 + 3x −10 = 0 .
Корнями этого уравнения являются числа x1 = −5 и x2 = 2. Они и являются нулями функции. График функции f (x)
пересекается с осью абсцисс в точках A1 (−5;0) и A2 (2;0). Найдем f (0).
f (0)= 10 − 3 0 −02 = 10.
График пересекается с осью ординат в точке B (0;10).
Определим интервалы знакопостоянства. Разобьем числовую прямую (область определения функции) на интервалы в точках
x1 = −5 и x2 = 2 (нули функции) (рис. 2.3.10).
Рис. 2.3.10
Найдем знаки функции f (x) на каждом интервале. f (−6 )= 10 − 3 (−6 )−(−6 )2 = 10 + 18 − 36 = −8 < 0.
f (−1)= 10 − 3 (−1)−(−1)2 = 10 + 3 −1 = 12 > 0. f (3)= 10 − 3 3 − 32 = 10 −9 −9 = −8 < 0.
121
Таким образом, функция положительна при x (−5; 2) и отрицательна при x (−∞;−5)U (2;+∞).
4) Найдем производную функции f (x):
f ′ (x)= (10 − 3x − x2 )′ = −3 − 2 x.
Приравняем производную к нулю и решим полученное урав-
нение.
−3 − 2 x = 0 x = −1,5.
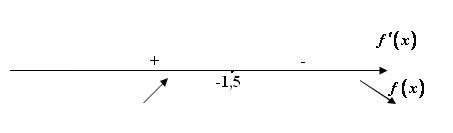
Это критическая точка функции. Разобьем в этой точке область определения на интервалы (рис. 2.3.11).
Рис. 2.3.11
Найдем знак производной на каждом из интервалов. f ′ (−2)= −3 − 2 (−2)= 1 > 0.
f ′ (0)= −3 − 2 (0)= −3 < 0.
Таким образом, функция возрастает на интервале (−∞;−1,5) и убывает на интервале (−1,5;+∞). Точка M (−1,5;12,25) является точкой максимума.
5) Найдем вторую производную функции f (x). f ′′(x)= (−3 − 2 x)′ = −2.
122
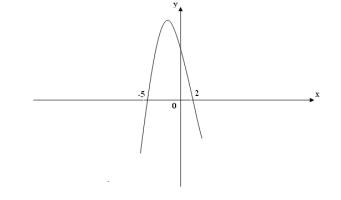
График функции f (x) является выпуклым на всей числовой
прямой, так как вторая производная отрицательна. Точек перегиба нет.
6) Вертикальных асимптот нет, поскольку областью определения является множество всех действительных чисел.
Найдем пределы функции при x → −∞ и при x → +∞
lim |
f (x)= lim |
( |
10 − 3x − x |
2 |
) |
= −∞. |
||||||
x→−∞ |
|
|
x→−∞ |
|
|
|
|
|
|
|
||
lim |
f (x)= lim |
( |
10 − 3x − x |
2 |
) |
= −∞. |
||||||
x→+∞ |
|
|
x→+∞ |
|
|
|
|
|
|
|
||
Горизонтальных асимптот нет. |
f (x) |
|
|
|
|
|||||||
Найдем пределы |
функции |
|
|
при x → −∞ и при |
||||||||
|
|
x |
||||||||||
x → +∞ |
|
|
|
|
|
|
|
|
|
|
||
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
= lim |
|
10 |
− 3 − x |
= +∞. |
||||||
|
x |
x |
||||||||||
x→−∞ |
|
x→−∞ |
|
|
|
|
|
|||||
lim |
|
f (x) |
= lim |
|
10 |
− 3 − x |
= −∞. |
|||||
|
x |
x |
||||||||||
x→+∞ |
|
x→+∞ |
|
|
|
|
|
|||||
Наклонных асимптот нет. Таким образом, функция f (x)
асимптот не вообще имеет. 7) График функции.
Рис. 2.3.12
123
Пример 2.3.15. Исследовать функцию и построить график: f (x)= 16 −8 x2 .
Решение.
1) Областью определения функции является множество
(−∞;−4)U (−4;4)U (4;+∞).
2)Проверим функцию на четность.
f (−x)= |
|
8 |
= |
|
8 |
= f (x). |
|
−(−x)2 |
16 |
− x2 |
|||
16 |
|
|
||||
Функция четная.
3) Найдем нули функции. Уравнение
8 |
= 0 |
|
16 − x2 |
||
|
не имеет решений. С осью абсцисс график не пересекается. Найдем f (0).
f(0)= 16 8−02 = 0,5.
Сосью ординат график пересекается в точке B (0;0,5).
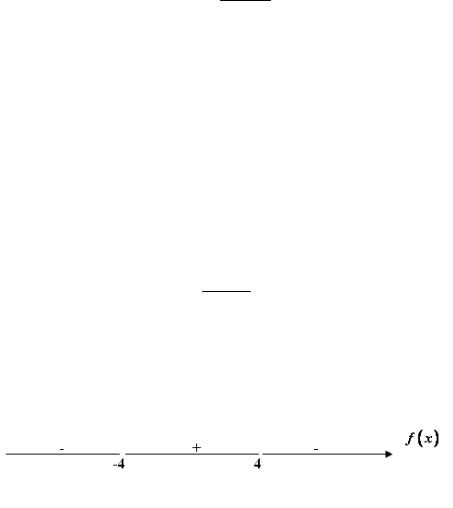
Рассмотрим область определения функции (нулей у функции нет) и определим знак функции на каждом из интервалов (рис. 2.3.13).
Рис. 2.3.13
124
f (−5)= |
|
|
|
|
8 |
|
|
|
= − |
8 < 0. |
|||
16 |
−(−5)2 |
||||||||||||
|
|
|
|
9 |
|||||||||
f (0) |
= |
|
8 |
|
= |
|
1 |
> 0. |
|||||
16 −02 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
||||||
f (5)= |
|
|
8 |
|
= − 8 |
< 0. |
|||||||
16 −52 |
|||||||||||||
|
|
|
|
|
9 |
|
|||||||
Функция положительна при x (−4;4) и отрицательна при x (−∞;−4)U (4;+∞).
4) Найдем производную функции:
|
8 |
|
′ |
16 x |
|
|
|
f ′(x)= |
|
|
|
= |
|
|
. |
16 − x |
2 |
(16 − x2 ) |
2 |
||||
|
|
|
|
|
|
||
Приравняем производную к нулю и решим полученное урав-
нение:
16 x |
= 0 x = 0. |
(16 − x2 )2 |
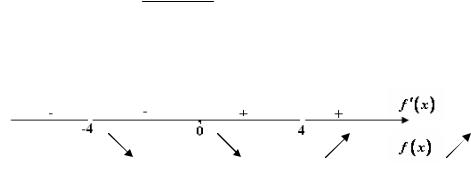
Разобьем область определения на интервалы в критической точке x = 0 (рис.2.3.14)
Рис. 2.3.14
Функция убывает на множестве (−∞;−4)U (−4;0) и воз-
растает на множестве (0;4)U (4;+∞).
5) Найдем вторую производную функции f (x).
125
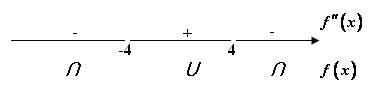
|
|
|
|
16 x |
′ |
|
16 (16 − x |
2 |
) |
2 |
− 32 x (16 |
− x |
2 |
)(−2 x) |
|
||
f |
′′ |
(x)= |
|
|
= |
|
|
|
= |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
(16 − x2 )2 |
|
|
|
(16 − x2 )4 |
|
|
|
||||||||
|
16 (16 − x2 )+64 x2 |
|
|
256 + 48 x2 |
|
|
|
|
|
|
|
|
|||||
= |
|
|
|
= |
(16 − x2 )3 . |
|
|
|
|
|
|
|
|||||
|
(16 − x2 )3 |
|
|
|
|
|
|
|
|
||||||||
Приравняем вторую производную к нулю и решим полученное уравнение.
256 + 48 x2 = (16 − x2 )3 0.
Это уравнение корней не имеет и, следовательно, нет точек перегиба. Рассмотрим область определения (за отсутствием точек перегиба).
Рис. 2.3.15
График функции является выпуклым вверх на множестве (−∞;−4)U (4;+∞) и выпуклым вниз на множестве (−4;4). Точек
перегиба нет. |
|
|
|
|
|
|
|
||
|
6) Проверим на наличие вертикальной асимптоты точки раз- |
||||||||
рыва x1 = −4 и x2 |
= 4. |
|
|
|
|
|
|
||
lim |
f (x)= lim |
8 |
= |
8 |
= |
8 |
|
= −∞. |
|
16 − x2 |
16 −(−4 −0)2 |
16 −16 − |
8 0 −02 |
||||||
x→−4−0 |
x→−4−0 |
|
|
|
|||||
126
