
Ольков_С_Г_Аналитическая юриспруденция
.pdf
индекс i – от 1 до n, где p – число столбцов в таблице, а n – число строк; N=p∙n. Символ åå – двойная сумма (все значения таблицы складываются и делятся на общее число элементов таблицы).
Статистическим распределением (statistical distribution)
случайной величины X (распределением изучаемого признака по частотам встречаемости) считаем таблицу значений признака (х), расположенного в возрастающем порядке и соответствующих им значений частот (абсолютная частота) или частостей (относительная частота). То есть статистическое распределение
отвечает на вопрос, как часто встречаются соответствующие значения исследуемого признака расположенного в ранжированном порядке. Например, если мы изучаем рецидивную преступность (х), то число лиц с количеством прежних судимостей одна и более отражает частоту встречаемости рецидивистов в изучаемой выборке (f или w).
Меры центральной тенденции как бы показывают центр
тяжести |
исследуемого |
вариационного |
ряда, |
«центростремительность» его элементов. Сюда относятся различные виды математических ожиданий и средних, мода, медиана.
Все средние величины делят на две группы: 1) степенные средние; 2) структурные (непараметрические) средние.
Степенные средние – обобщающие показатели вариационных рядов, показывающие их «центр тяжести».
Средняя степенная простая:
|
|
|
n |
x k |
|
|
|
Х = k å |
|
, где |
k – показатель степени, изменяющийся в |
||||
i |
|
||||||
n |
|||||||
|
|
|
i=1 |
|
|
|
|
пределах [-1; +∞], хi – варианты, n – число вариант (число наблюдений или рабочих строк в таблице). Простая средняя степенная применяется, когда веса вариант равны, например, в случае, когда каждая варианта встречается только один раз.
Средняя степенная взвешенная:
|
|
|
n |
x k × f |
|
|
|
|
|
Х = k å |
i |
|
, где |
k – показатель степени, хi – варианты, n – |
|||||
i |
|
|
|||||||
|
n |
|
|||||||
|
|
|
i=1 |
|
|
|
|
|
|
число вариант (число наблюдений или рабочих строк в таблице), fi
– частота, вес (показатель повторяемости вариант в вариационном
72
ряду). Применяется, когда веса вариант различны по сгруппированным рядам.
Поскольку k – показатель степени, изменяется в пределах [-1; +∞], постольку выделяют среднюю гармоническую, где k=-1, среднюю геометрическую, где k=0, среднюю арифметическую, где k=1, среднюю квадратическую, где k=2, среднюю кубическую, где k=3, среднюю биквадратическую, где k=4.
Существует правило мажорантности: величина степенной средней более высокой степени всегда больше или равна величине средней рассчитанной по формуле с меньшей степенью. То есть средняя гармоническая меньше или равна средней геометрической, средняя геометрическая меньше или равна средней арифметической и т.д.
При вычислении средней величины в вариационных рядах с равными интервалами применяют метод моментов. Здесь расчет средней осуществляется по формуле: Х = i × M1 + A , где
M1 = å[(xi - A) / i × fi ]/ å fi , где М1 – момент первого порядка; i – длина интервала, A – центральная варианта ряда (условный нуль).
Моментом k-го порядка называется средняя из k-ых степеней отклонений вариантов переменной х от постоянной A. Подробнее об этом говорится в специальных курсах по теории вероятностей и некоторых работах по теории статистики29.
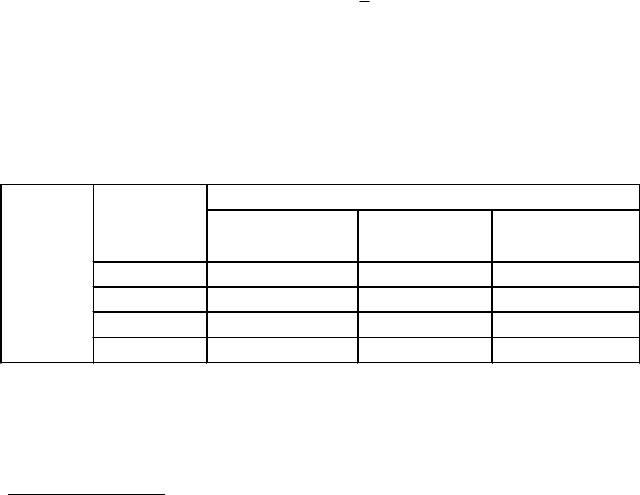
|
|
Виды моментов |
|
|
Начальные |
Центральны |
Условные |
Порядок |
|
е |
|
Первый |
М1 |
μ1 |
m1 |
Второй |
М2 |
μ2 |
m2 |
Третий |
М3 |
μ3 |
m3 |
Четвертый |
М4 |
μ4 |
m4 |
М1 = |
åхi fi |
= x |
– начальный момент первого порядка. По сути, это |
|
å fi |
||||
|
|
|
среднее взвешенное.
29 Теория статистики: учебник / Р.А. Шмойлова, В.Г. Минашкин, Н.А.Садовников, Е.Б.Шувалова; под ред. Р.А. Шмойловой. – 4-е изд., перераб. и доп. – М.: Финансы и статистика, 2004. С. 259-262.
73
|
|
|
åхi |
2 |
fi |
|
|
|
|
|
|
|
|
– начальный момент второго порядка. По сути, это |
М 2 |
= |
|
|
|
=x |
2 |
||||||||
|
å fi |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
средне взвешенный квадрат переменной икс. |
||||||||||||||
|
|
|
åхi |
3 |
fi |
|
|
|
|
|
|
|
– начальный момент третьего порядка. По сути, это |
|
М 3 |
= |
|
|
|
=x |
3 |
|
|
||||||
|
å fi |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
средне взвешенный куб переменной икс. |
||||||||||||||
|
|
|
åхi |
4 |
fi |
|
|
|
|
|
– начальный момент четвертого порядка. По сути, |
|||
М 4 |
= |
|
|
|
=x |
4 |
||||||||
|
å fi |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
это средне взвешенный икс в четвертой степени.
Среди начальных моментов самостоятельное значение имеет только первый. Второй, третий и четвертый моменты имеют вспомогательное значение и используются при вычислении центральных моментов.
μ1 |
= |
å(хi - х) × fi |
= 0 |
|
– центральный момент первого порядка. Всегда |
|||||||||
|
|
|||||||||||||
|
|
å fi |
|
|
|
|
|
|
|
|
|
|
|
|
равен нулю. |
|
|
|
|
|
|
|
|
|
|
||||
μ2 |
= |
å(хi - х)2 |
× fi |
= σ |
2 |
– центральный момент второго порядка являет |
||||||||
å fi |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
собой дисперсию. |
|
|
|
|
|
|
||||||||
μ3 |
= |
å(хi - х)3 |
× fi |
= Асим |
– |
центральный |
момент третьего |
порядка |
||||||
å fi |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
являет собой меру асимметрии. |
|
|
|
|
||||||||||
μ4 |
= |
å(хi - х)4 |
× fi |
|
= Эксц |
– |
центральный |
момент |
четвертого |
порядка |
||||
å fi |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
являет собой меру эксцесса. |
|
|
|
|
||||||||||
m1 |
= |
å(хi - A) × fi |
|
|
|
– |
условный |
момент |
первого |
порядка. |
||||
å fi |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
= |
å(хi - A) |
2 × fi |
– условный момент второго порядка. |
|
|||||||||
å fi |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m3 |
= |
å(хi - A) |
3 × fi |
– условный момент третьего порядка. |
|
|||||||||
å fi |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m4 |
= |
å(хi - A) |
4 × fi |
– условный момент четвертого порядка. |
|
|||||||||
å fi |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74

Условные моменты не имеют самостоятельного значения, а используются для упрощения вычислений центральных моментов.
Структурные средние используются для исследования внутреннего строения рядов распределения изучаемого признака. Сюда относят: моду (величина признака (варианта, переменной), которая чаще всех других признаков встречается в изучаемой совокупности), медиану (варианта, находящаяся в середине вариационного ряда), квартили (делят ранжированный ряд на 4 равные части), децили (делят ранжированный ряд на 10 равных частей), квинтили (делят ранжированный ряд на 5 равных частей), перцентили (делят ранжированный ряд на 100 равных частей).
Простое среднее арифметическое30 является наиболее распространенной оценкой среднего значения распределения и вычисляется по формуле:
|
|
|
n |
|
|
|
|
|
|
åхi |
= x1 + x2 + ... + xk |
|
|
|
Х |
= i=1 |
, где n – объем выборки. Если вычисления |
|||
|
|
|
n |
|
n |
|
проводятся по генеральной совокупности (ГС), то вместо n, берется N – объем генеральной совокупности и вместо выборочного среднего арифметического получается среднее арифметическое для ГС, которое называют математическим ожиданием.
P.S. Величина среднего арифметического зависит от всех элементов, содержащихся в числителе, поэтому наличие их скачков (выбросы или экстремальные значения) снижает качество оценки. В этом случае лучше использовать медиану.
Простое математическое ожидание (population mean) для дискретных данных вычисляется точно также как и среднее арифметическое:
|
n |
|
|
|
|
μ = |
å хi |
= |
x1 + x2 + ... + xk . |
||
i 1 |
|||||
= |
|
|
|||
N |
N |
||||
|
|
||||
Медиана (median) – число, разделяющее ранжированную выборку или ГС пополам. То есть 50% выборочных данных меньше медианного значения, и 50% - больше медианы.
n +1
M= 2 – если выборка содержит нечетное число элементов.
30 Принимаем, что вероятности исходов (событий, значений) равные. Это очевидно, когда числовые значения не повторяются.
75

Втом случае, когда выборка содержит четное число элементов, то медиана расположена между двумя средними элементами выборки и равна их среднему арифметическому: (x1 + x2)/2.
Впрограмме Excel имеется функция МЕДИАНА. Достаточно взять любой временной или пространственный ряд (даже не
ранжированный), войти в мастер функций (fх), выбрать категорию статистические, и в статистических функциях - функцию МЕДИАНА. Чтобы не вводить чисел в окне функции – просто
выделить курсором, удерживая левую клавишу мыши, ряд, содержащий исходные данные, и нажать клавишу ОК в окне функции. Аналогичным образом находятся квартили – первый, второй, третий и четвертый. Здесь нужно взять функцию
КВАРТИЛЬ (Массив, Часть). В строку Массив ввести значения ряда, а в строке Часть указать № квартиля, например, 1. Найти значение моды можно с помощью функции МОДА.
Использование программы Excel (или любой другой подходящей программы) весьма удобно при работе с длинными рядами.
Для дискретного ряда мода находится непосредственно путем выбора числа, встречающегося наиболее часто. Для интервального ряда с равными интервалами и с неравными интервалами имеются специальные интерполяционные формулы вычисления моды, разработанные Р.М. Орженцким (1863-1923)31:
1) для интервального ряда с равными интервалами:
Мо = xk 1 +hk × |
fk - fk −1 |
|
, где Мо – мода, хk-1 – нижняя |
− |
( fk - fk −1 ) +( fk |
- fk +1 ) |
|
граница модального интервала, hk – длина модального интервала, fk- 1, fk и fk+1 – частота интервала предшествующего модальному, модального и следующего за модальным;
2) для интервального ряда с неравными интервалами:
Мо = xk 1 + hk × |
|
yk - yk −1 |
|
, |
где вместо |
частот |
(f) |
взята |
||
|
|
|
||||||||
− |
( yk - yk −1 ) + ( yk |
- yk +1 ) |
|
|
|
|
|
|
|
|
плотность распределения (Y или y). |
|
|
|
|
|
|
||||
Абсолютная плотность распределения – это частота, |
||||||||||
приходящаяся на |
единицу |
длины |
интервала: |
Yi = |
fi |
, |
где |
Yi – |
||
h |
||||||||||
|
|
|
|
|
|
|
i |
|
|
|
абсолютная плотность распределения, fi – частота, hi – длина интервала.
31 Теория статистики: Учебник/ Под ред. проф. Г.Л. Громыко. – 2-е изд., перераб. и доп. – М.: ИНФРА-М, 2006. С. 100-101.
76

Относительная плотность распределения – это частость,
приходящаяся на единицу длины интервала: yi = whi , где yi –
i
относительная плотность распределения, wi – частоcть, hi – длина интервала.
Задача №1.
Дано: выборка лиц, ранее судимых за совершение различных преступлений (рецидивисты).
xi |
|
|
|
|
|
|
Число судимостей |
6 |
5 |
4 |
3 |
2 |
1 |
fi |
|
|
|
|
|
|
Число лиц |
8 |
12 |
19 |
24 |
35 |
43 |
Требуется: найти моду.
Ответ: Мо=1. В вариационном ряду число «1» встречается 43 раза (больше всех). Интерпретация: «модной» в данном ряду является одна судимость, поскольку она встречается наиболее часто.
Задача №2.
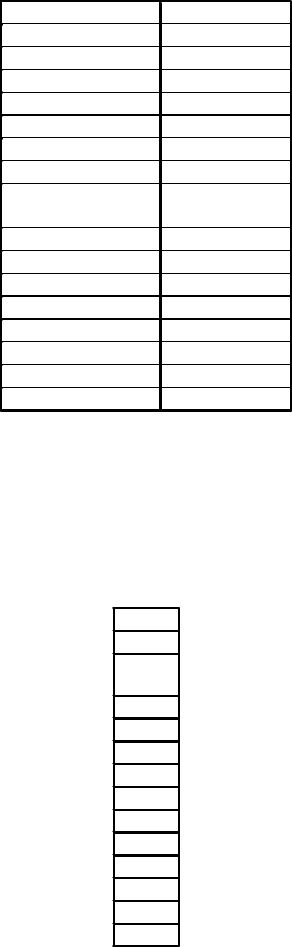
Дано: таблица первичных статистических данных о числе зарегистрированных по территории Украины хулиганств в 2009 году.
|
Хулиганство |
|
(Хулiганство), |
Субъект Украины |
шт. |
|
(2009 г.) |
|
|
|
|
АР Крим |
419 |
|
|
Вінницька |
374 |
|
|
Волинська |
441 |
|
|
Дніпропетровська |
599 |
|
|
Донецька |
1774 |
|
|
Житомирська |
321 |
|
|
Закарпатська |
305 |
|
|
Запорізька |
337 |
|
|
Івано- |
|
Франківська |
303 |
|
|
Київська |
159 |
|
|
77
місто Київ |
463 |
|
|
Кіровоградська |
146 |
|
|
Луганська |
666 |
|
|
Львівська |
597 |
|
|
Миколаївська |
222 |
|
|
Одеська |
271 |
|
|
Полтавська |
162 |
|
|
Рівненська |
125 |
|
|
місто |
|
Севастополь |
79 |
|
|
Сумська |
349 |
|
|
Тернопільська |
227 |
|
|
Харківська |
955 |
|
|
Херсонська |
147 |
|
|
Хмельницька |
305 |
|
|
Черкаська |
138 |
|
|
Чернігівська |
127 |
|
|
Чернівецька |
266 |
Требуется: найти моду в данном вариационном ряду, и дать её интерпретацию. Сравнить моду со средним арифметическим значением вариационного ряда. Построить график ранжированных данных вариационного ряда, и на него нанести линии среднего арифметического и моды.
Решение:
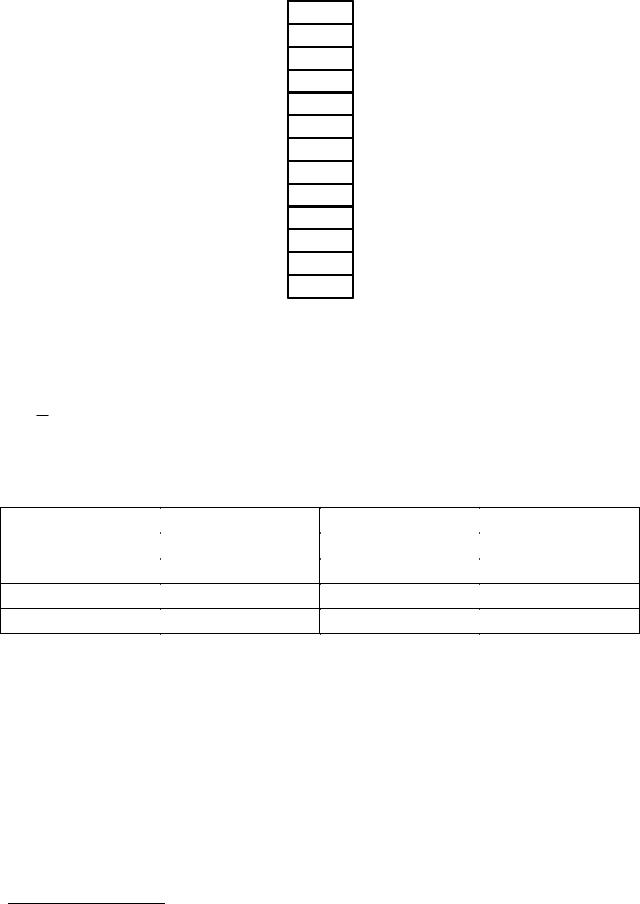
1) Ранжируем вариационный ряд:
79 
125
127 
138
146 
147
159 
162
222 
227
266 
271
303 
305
78
305 
321
337 
349
374 
419
441 
463
597 
599
666 
955
1774
2)По формуле Стерджесса определим число интервалов: k=1+3,322∙log (N)= 1+3,322∙log (27)=5,75≈6.
3)По формуле вычислим длину (шаг) интервала32:
h = R = 1774 −79 = 282,5 ≈ 300 . k 6
4) Учитывая особенности вариационного ряда, будем работать с тремя неравными интервалами (h).
|
h, сотен шт. |
|
fi |
wi |
yi |
|||
|
|
0,7-3,09 |
|
|
|
15 |
55,55% |
23,24 |
|
|
3,1-6 |
|
|
|
9 |
33,33 |
11,49 |
|
6,1-17,75 |
|
|
|
3 |
11,11% |
0,95 |
|
|
|
ИТОГО |
|
|
27 |
|
|
|
y1 |
= |
55,55 |
|
= 23,24 . |
|
|
|
|
(3,09 -0,7) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Мо =0,7 +2,39 × |
|
|
23,24 −0 |
=2,28. |
|
|||
(23,24 -0) +(23,24 -11,49 ) |
|
|||||||
Ответ: мода составляет 228 шт. Интерпретация: наиболее типичным в 2009 году на территории Украины было число, колеблющееся около 228 хулиганств. Среднее число преступлений данной структурной составляющей преступности равнялось 380 штукам. То есть мода оказалась меньше среднего значения, что следует принимать во внимание, поскольку мода – структурное среднее. Типичным для субъектов Украины в 2009 году был
32 Существуют различные способы определения длины интервала. Например, в программе Excel, если не задать иного, то будет выполняться процедура:R/√n, где n – число наблюдений.
79
сравнительно невысокий уровень хулиганства, колеблющийся около 228 преступлений. Ориентация на среднее арифметическое в данном случае приведет к ошибочным выводам, и завышенным оценкам числа совершаемых преступлений.
Выборочная средняя ( Х ) при наличии повторяющихся значений признака рассчитывается как обычная средняя взвешенная по частотам или частостям.
Если имеет место не дискретное, а непрерывное распределение, то следует рассчитывать математическое ожидание или вместо
переменной х брать середины интервалов: хi + xi+1 .
2
При больших значениях выборочных данных иногда удобно перейти от абсолютных значений переменной икс к их суррогатам
zi, рассчитываемым, например, по формуле: z = xi -G , где G – новая,
i h
смещенная точка отсчета, скажем, значение переменной х с наибольшей частотой f, h - сумма частот f. В таком случае в обычном порядке рассчитывается новая средняя взвешенная Z , которая связана с обычной средней взвешенной полученной по выборочным данным формулой: X = Zh +G .
Среднее геометрическое (geometric mean) простое – это корень энной степени из произведения n величин. Вычисляется по
формуле: Х |
= (x × x |
×...× x )n |
= n x × x |
|
×...× x |
|
или в другой записи: |
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Г |
1 2 |
n |
|
1 |
2 |
|
n |
||
1
Хæ∏n x ön .
Г= ç i ÷
è i=1 ø
Среднее геометрическое (geometric mean) взвешенное:
ХГвз
ХГвз
æ |
n |
|
ö |
1 |
или: |
wi |
åin 1 wi |
||||
= ç |
∏xi |
|
÷ |
= |
|
è i=1 |
|
ø |
|
|
|
æ 1
=exp çç ån w ×åin=1 wi è i=1 i
ö
ln xi ÷÷, где w – веса (доли), соответствующих
ø
значений переменной х.
Как известно среднее арифметическое не показывает отсутствие изменений, происходящих с наблюдениями с течением времени. Этого недостатка лишено среднее геометрическое.
Среднее геометрическое значение нормы прибыли (geometric rate of return) – вычисляется по формуле:
|
|
|
|
|
1 |
|
|
|
|
|
= [(1+ R )×(1+ R ) + ...+ (1+ R )]n |
-1, где R – норма прибыли за |
i-й |
||
R |
Г |
||||||
|
|
1 |
2 |
n |
|
|
|
период времени.
80

Среднее геометрическое значение нормы прибыли позволяет оценить степень отсутствия изменений переменной с течением времени. Покажем это на примере33. Предположим, что объем вложенных средств в исходный момент равен 100 тысяч рублей. К концу первого года он падает до уровня 50 тысяч рублей, а к концу второго года восстанавливается до отметки 100 тысяч рублей. Если вычислить простое среднее, то получится норма прибыли равная
25%: |
|
= −0,5 +1 |
= 0,25 . |
То есть простое |
среднее |
игнорирует |
Х |
||||||
2 |
|
|
|
|
||
изменение, где за |
первый год норма |
прибыли |
составила: |
|||
R1 = 50000 −100000 |
= −0,5 , а за второй год: R2 = 150000 −50000 =1. |
|
||||
100000 |
|
|
100000 |
|
||
Рассчитывая среднее геометрическое нормы прибыли, получим:
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г = [(1- 0,5)× (1+ 1))]2 -1 = 0 , что и соответствует действительности. |
|
|||||||||||||||||
R |
|
||||||||||||||||||||
Рассчитывая среднее геометрическое, получим: |
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Г = (-0,5×1)2 = 0,7 . |
|
|
|
|
|
|
|
|
|
|
|||||||||
Х |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
Среднее |
гармоническое простое: |
X гарм = |
|
, где X гарм |
- |
||||||||||||
|
|
|
|
å 1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
x |
i |
|
|
|
|
средняя гармоническое. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Среднее гармоническое взвешенное: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
åwi |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
X |
гармВз = |
i=1 |
|
, где |
|
гарВз - средняя гармоническая взвешенная, wi |
||||||||||
|
|
|
|
|
|
X |
|||||||||||||||
|
|
|
|
|
n |
w |
|||||||||||||||
|
|
|
|
|
|
|
å xi |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
i=1 |
i |
|
|
|
|
|
|
|
|
|
|
|||
=xi∙fi , где f - частота встречаемости.
Среднее гармоническое взвешенное:
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
åxi |
, |
где |
X гармВз - |
средняя |
гармоническая |
||||||
X гармВз = n |
i=1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
å |
|
xi |
|
|
|
|
|
|
|
|
|
|
|
Тр(ц) |
i |
|
|
|
|
|
|
||||
|
i=1 |
|
|
|
|
|
|
|
|
|||
взвешенная.
Среднее гармоническое применяется: 1) когда известны варьирующие обратные значения изучаемой переменной; 2) когда известны сводные (обобщающие) величины, например, в сельском
33 Статистика для менеджеров с использованием Microsoft Excel, 4-е изд.: Пер. с англ. – М.: Издательский дом «Вильямс», 2004. С. 187.
81
