
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Ольков_С_Г_Аналитическая юриспруденция
.pdf

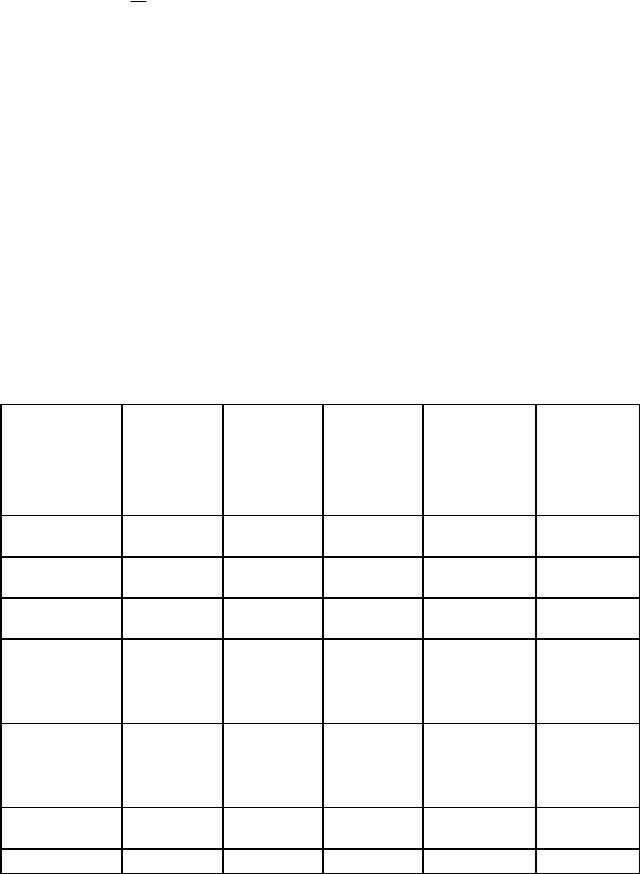
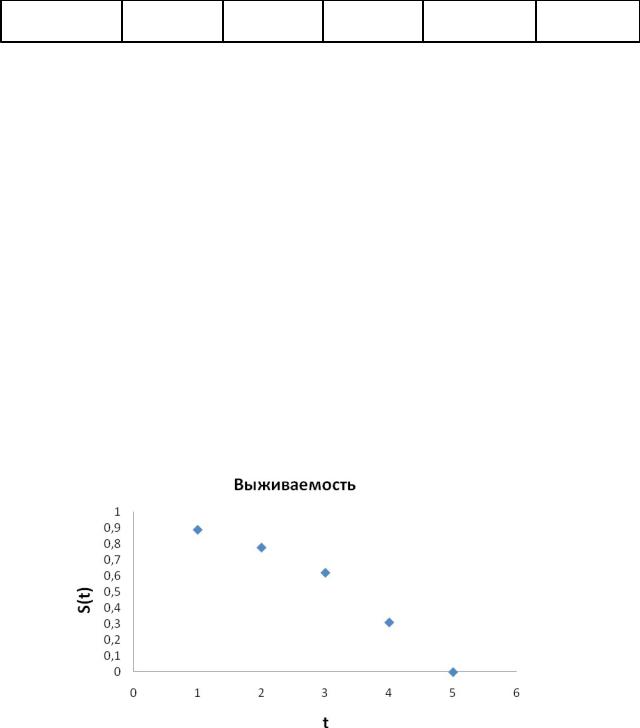
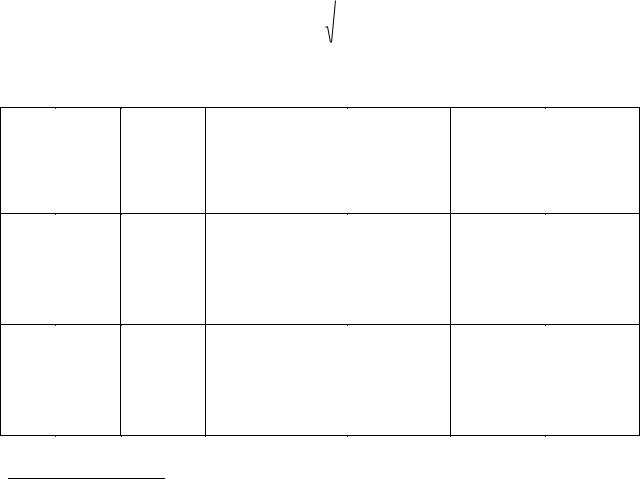
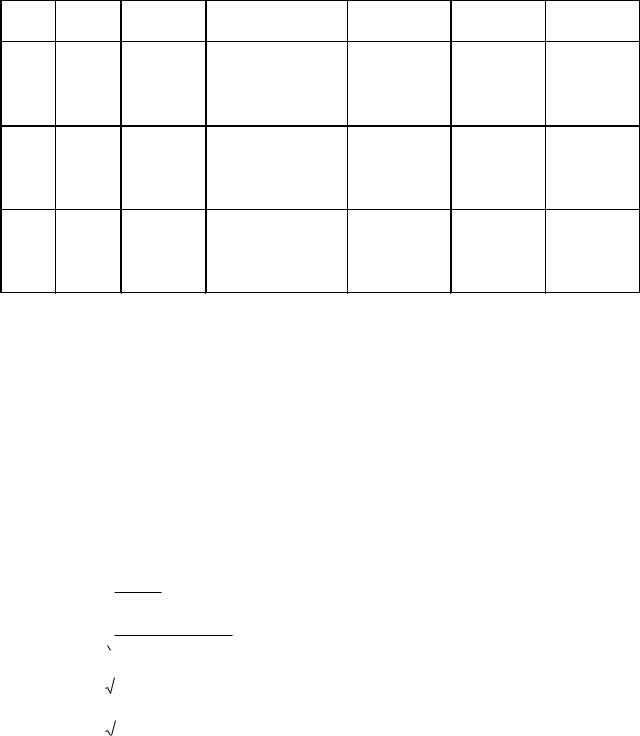



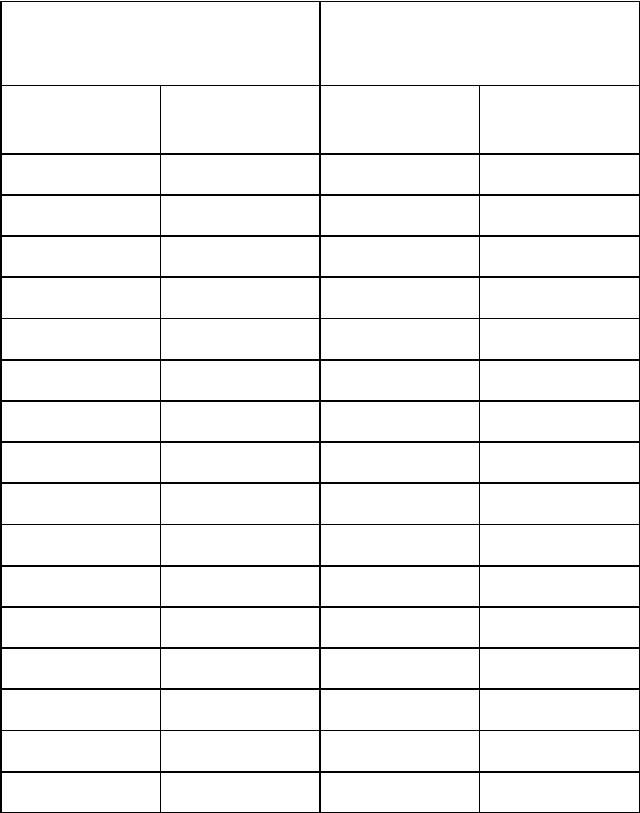
Решим задачу, поясняющую теорию. Пусть у нас имеется две выборки. Выборка №1, включающая группу из 20 наблюдаемых (n1=20), и выборка №2, включающая 17 наблюдаемых (n2=17). Нам нужно проверить различие двух методик кадровой работы с сотрудниками полиции. Составим таблицу.
Методика №1 |
Методика №2 |
||
Первая группа (n=20) |
Первая группа (n=17) |
||
Время, мес. |
Число |
Время, мес. |
Число |
|
увольнений |
|
увольнений |
3 |
2 |
5 |
1 |
5 |
1 |
8+ |
1 |
7 |
1 |
12 |
2 |
8 |
1 |
15 |
1 |
9+ |
1 |
16 |
1 |
11 |
2 |
23 |
1 |
13 |
1 |
27 |
2 |
15 |
1 |
29 |
1 |
16 |
1 |
32 |
2 |
20 |
2 |
33+ |
1 |
21 |
1 |
35 |
2 |
24+ |
1 |
39 |
1 |
27 |
1 |
40 |
1 |
30+ |
1 |
|
|
33 |
1 |
|
|
34+ |
1 |
|
|
206
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]


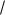 0,0138
0,0138 
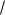 (0,0138
(0,0138