SalimovRB_matematika_gl_1-9_2011_web

Она симметрична с прямой (43) относительно Ox, проходит через точку O 0, 0 и через точку K a, b , симметричную с K относительно Ox. В силу

симметрии гиперболы относительно оси абсцисс ясно, что гипербола по отношению к прямой (44) расположена аналогично её расположению к прямой (43). Прямые (43) и (44) называются асимптотами.

При построении гиперболы целесообразно сначала начертить ее асимптоты. Точки A1 a, 0 и A2 a, 0 пересечения гиперболы с осью Ox называются

вершинами гиперболы. Расстояние между ними равно 2a , A1 A2 называется

действительной осью гиперболы; B1B2 2b и называется мнимой осью.

§ 15. Парабола

Параболой называется геометрическое место точек на плоскости, равноудалённых от заданной точки, называемой фокусом, и заданной прямой, называемой директрисой. Пусть F – фокус. Ось Ox проведём через F перпендикулярно директрисе (рис. 26).

Пусть p – расстояние от фокуса F до директрисы. Это число задано и называется параметром параболы. Начало координат возьмём в середине перпендикуляра,

уравнение x p / 2 . Пусть M x, y – произвольная точка

параболы, N – основание перпендикуляра, опущенного из точки M на директрису. Из рис. 26 видно, что расстояние

41

5354.ru

Запишем расстояние от F до M :

FM x p / 2 2 y 0 2 (46)

Для любой точки M параболы имеем MN FM (по определению). Подставим сюда выражения (45), (46) и получим уравнение параболы

p / 2 x x p / 2 2 y2 .

Упростим его, избавляясь от корня. Получим каноническое уравнение парабо-

лы

Исследуем форму параболы по уравнению (47). Так как это уравнение содержит y только во второй степени, то, как и в случае эллипса, Ox является осью симметрии параболы. Следовательно, вид параболы достаточно установить в верхней полуплоскости, где y 0 . Для таких значений y уравнение

точка M совпадает с 0, 0 . С увеличением x – абсциссы точки M – её ордината, равная 2 px , неограниченно растёт, и точка M уходит вверх и вправо.

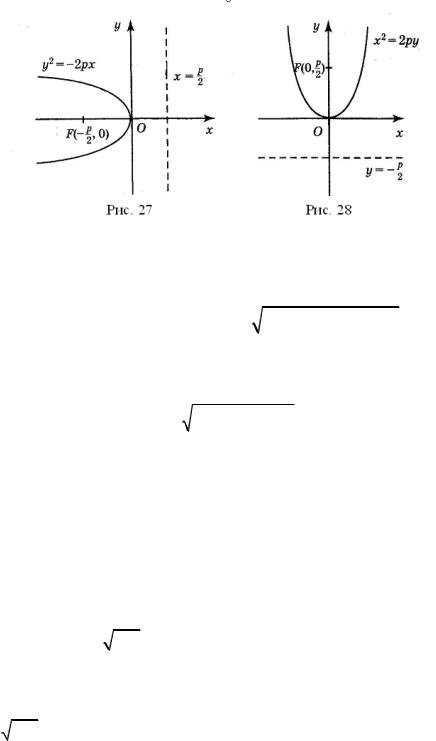
В силу симметрии остальная часть параболы вычерчивается сразу. Если Ox провести от F к директрисе, то получим параболу, изображенную на рис. 27. Легко проверить, что уравнение параболы в этом случае будет иметь вид Пусть теперь ось Oy направлена перпендикулярно к директрисе и

42

5354.ru

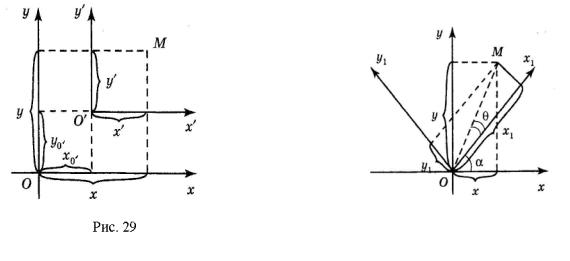
проходит через F . При этом уравнение параболы будет иметь вид x2 2 py

(см. рис. 28).

§ 16. Преобразование координат на плоскости

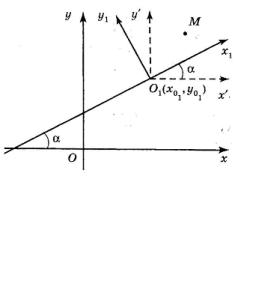
Параллельный перенос осей координат. Пусть Oxy – исходная система координат, O ' x ' y ' – новая система координат, полученная параллельным переносом исходной системы, как показано на рис. 29. Положение новой системы по отношению к старой определим, задав координаты O ' xo ' , yo ' нового начала O ' в старой системе координат, где xo' , yo' – заданные числа. Пусть x ' ,

Рис. 30

Поворот осей координат. Пусть Oxy – исходная система координат, а новая система координат получена поворотом исходной вокруг начала координат на угол , где – заданное число (см. рис. 30). Угол берётся со знаком «+», если отсчёт ведётся против хода часовой стрелки от оси Ox. Пусть x, y – координаты точки M в системе Oxy , x1, y1 – координаты точки M в системе Ox1 y1 . Пусть OM и – угол, образованный отрезком OM с осью Ox1 , причём, как и , этот угол берётся со знаком «+», если отсчёт ведётся от оси Ox1 против хода часовой стрелки. Из рис. 30 видно, что

Формулы (50) перепишем, использовав известные формулы тригонометрии

Эти формулы выражают старые координаты точки M x, y через её новые координаты в случае поворота осей координат.

Общий случай. Пусть Oxy – исходная система координат, O1 x1 y1 – новая

система координат (рис. 31). Положение новой системы по отношению к старой определим, задав:

координаты xo1 , yo1 нового начала O1 в старой системе координат;

угол , который образует ось O1x1 с Ox.

Так как система координат O1x ' y ' получена параллельным переносом Oxy , то координаты x, y точки M в исходной системе выражаются через координаты

44

5354.ru

Эти формулы выражают старые координаты x, y точки M через её новые координаты x1, y1 в новой системе.

Преобразования координат на плоскости применяются, в частности, для

уравнение эллипса в новой системе координат O1 x1 y1 . Это будет уравнение общего вида (после раскрытия скобок)

Ax12 2Bx1 y1 Cy12 2Dx1 2Ey1 F 0 .

Таким образом, перейдя к системе O1 x1 y1 , от канонического уравнения (54)

эллипса мы перешли к более сложному уравнению – уравнению второй степени общего вида. Можно показать, что, наоборот, от последнего уравнения в системе O1 x1 y1 , подобрав другую систему координат Oxy, можно получить ка-

ноническое уравнение, определяющее либо окружность, либо эллипс, либо

определяет лишь точку или не определяет никакого множества точек.

§ 17. Понятие о многомерном евклидовом пространстве

Известно, что положение точки на прямой определяется одним числом – её координатой, положение точки на плоскости определяется двумя числами

– координатами этой точки, а положение точки в пространстве – трёмя числами, её координатами. Обобщая эти представления, можно вести 4-мерное и т. д., n -мерное пространство. Таким путём можно построить n -мерную геометрию. Известно, что стереометрия основывается на системе аксиом – аксиоматике. Аналогично можно построить многомерную евклидову геометрию, взяв за основу аксиоматику, аналогичную аксиоматике стереометрии. Но ис-

45

5354.ru

торически многомерная геометрия была создана иначе, а именно, не на основании аксиом, аналогичных аксиомам стереометрии, а на основании так называемых координатных аксиом. Запишем их.

ствие положительное число, называемое расстоянием между этими точками и определяемое следующим образом:

MM x1 x1 2 x2 x2 2 xn xn 2 .

Геометрическими считаются лишь такие соотношения, которые связывают расстояния между точками и сохраняются при умножении всех расстояний на одно и то же число (как и при преобразовании подобия в стереометрии).

Теория, основанная на указанных аксиомах, называется n -мерной евклидовой геометрией. Множество точек M , для которых справедливы эти акси-

омы, называется n -мерным евклидовым пространством.

Пусть A, B – две точки в пространстве с координатами A x1A , x2A , , xnA и B x1B , x2B , , xnB . Вектором, у которого начало находится в точке A , а конец – в

точке B , назовём величину, обозначаемую AB ( AB a ), координаты которой равны разностям координат конца и начала (как в трёхмерном пространстве):

AB a x1B x1A , x2B x2A , , xnB xnA .

Вектор называется нулевым, если все его координаты равны нулю, в противном случае это ненулевой вектор.

Пусть даны два вектора a a1, a2 , , an и b b1,b2 , ,bn в n -мерном евклидовом пространстве. Они называются равными, если все их соответствующие координаты равны друг другу, т. е. ai bi для всех i 1, 2, , n .

Суммой этих векторов называется вектор, обозначаемый a b и опреде-

ляемый формулой a b a1 b1, a2 b2 , , an bn . Иначе говоря, при сложении векторов их соответствующие координаты складываются. Аналогично определяется разность векторов.

Произведением a на число называется вектор a a1, a2 , , an , т. е.

при умножении вектора на число на это число умножаются все его координаты.

46

5354.ru

векторами. Норма каждого из них равна единице, это видно из формулы (56).

a a1 e1 a2 e2 an en . Это есть разложение вектора a по базисным векторам в n -мерном пространстве.

Как и в трёхмерном пространстве, каждой точке M x1 , x2 , , xn будем ставить в соответствие её радиус-вектор r x1, x2 , , xn , концом которого является точка M , а началом – точка O 0, 0, , 0 .

Пусть в n -мерном пространстве заданы точка M0 своим радиус-вектором r0 и ненулевой вектор a . Прямой в этом пространстве называется множество

точек, радиус-векторы которых определяются формулой r r0 at , где t – скаляр (параметр), который принимает любые действительные значения.

Пусть в пространстве заданы точка M0 своим радиус-вектором r0 и два

ненулевых вектора a и b , для которых не выполняются условия коллинеар-

ности a1 / b1 a2 / b2 an / bn .

Плоскостью в n -мерном пространстве называется множество точек, ра-

диус-векторы которых определяются формулой r r0 at bs , где t , s – дей-

ствительные скалярные величины, принимающие любые действительные значения.

Аналогично можно ввести понятие сферы в n -мерном пространстве.

47

5354.ru

§ 18. Поверхности второго порядка. Сфера. Цилиндр

Поверхностью второго порядка в пространстве Oxyz называется по-

верхность, определяемая уравнением второй степени относительно текущих

координат a11x2 a22 y2 a33z2 2a12 xy 2a13 xz 2a23 yz 2a14 x 2a24 y 2a34 z a44 0.

Здесь a11, a22 , ... – действительные числа, называемые коэффициентами. В зависимости от коэффициентов это уравнение может определять поверхность

x0 , y0 , z0 , R – заданные числа (см. рис. 32). Раскрыв скобки и перенеся число

R2 в левую часть, получим

x2 y2 z2 2x0 x 2y0 y 2z0 z x02 y02 z02 R2 0.

Нетрудно проверить, что уравнение второй степени относительно x, y, z, в котором коэффициенты при x2 , y2 , z2 равны между собой, а члены с произве-

дениями координат отсутствуют, представляет собой уравнение сферы (если не имеет место случай, когда это уравнение не определяет поверхность).

Цилиндры второго порядка. Цилиндрической

называется поверхность, описываемая прямой, остающейся параллельной некоторому направлению и пересекающей данную линию. Последняя называется

направляющей цилиндрической поверхности, а прямая

– образующей.

Пусть, например, образующие цилиндрической поверхности параллельны оси Oz и направляющей служит эллипс (рис. 33) в плоскости Oxy с уравнением

48

5354.ru

Эта поверхность называется эллиптическим цилиндром. Пусть M (x, y, z) – произвольная точка этого цилиндра, а точка K(x, y) – проекция M на плоскость Oxy. Ясно, что абсциссы и ординаты точек M и K совпадают. Так как точка K лежит на эллипсе, то её координаты x и y удовлетворяют уравнению (57). Но тогда этому уравнению удовлетворяют координаты x и y точки M цилиндра. Значит, (57) есть уравнение цилиндра.

Итак, уравнение (57) на плоскости Oxy определяет эллипс, а в пространстве Oxyz – эллиптический цилиндр с образующей, параллельной Oz, направ-

плоскости Oxy получаем эллипс наибольших размеров. При | h | c значения a1 и b1 достигают наименьших значений a1 0 и b1 0. Это означает, что плоскости z c и z c имеют с эллипсоидом по одной общей точке (0,0,c) и (0, 0, c) соответственно. При | h | c эллипсоид с плоскостью z h общих точек не

При a b имеем эллипсоид вращения, поскольку в плоскости z h вместо эллипса получаем окружность. Эта поверхность получается при вращении

вокруг оси Oz эллипса ax22 cz22 1, расположенного в плоскости Oxz.

§ 20. Конус

Конусом второго порядка называется поверхность, определяемая уравнением

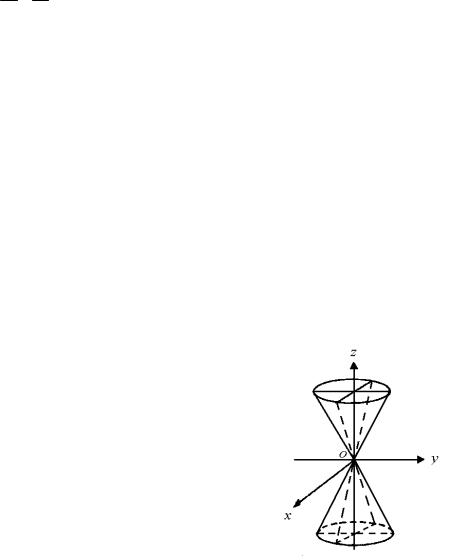
где a, b, c – заданные положительные числа (см. рис. 35). Исследовав форму

этой поверхности, как и эллипсоида, методом сечений, получим, что при сечении плоскостью z h ( h – постоянная) получается эллипс с полуосями a1 a | h |c и b1 b | h |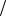c. Очевидно, что при h 0 a1 b1 0, т. е. конус (59) имеет с плоскостью Oxy одну общую точку – начало координат. С увеличением | h | значения a1 и b1 увеличиваются. Покажем теперь, что

при сечении поверхности (59) плоскостью с уравнением y kx ( k – постоянная), проходящей через Oz, получается пара прямых, проходящих через начало координат.

В самом деле, при таком сечении получается линия, определяемая системой уравнений

Но первое уравнение равносильно совокупности двух уравнений

50

5354.ru