1.Комбинаторика. История возникновения комбинаторики.
Дискретная математика возникла в результате развития и широкого распространения специфических методов исследования множеств, элементы которых могут быть перенумерованы. Простейшие из таких методов использовались еще в глубокой древности, когда мудрецы дальнего и ближнего Востока закладывали основы современной теории чисел. Выделяться же в самостоятельное научное направление дискретная математика начала с возникновением комбинаторного анализа, который сейчас именуется просто комбинаторикой. Именно с появлением этой дисциплины связывают историки зарождение дискретного анализа, ставшей впоследствии основой одного из крупнейших разделов современной математики.
Основоположниками комбинаторного анализа считаются французские математики Е.Паскаль и П.Ферма, опубликовавшие в XVII веке работы посвященные теории карточных игр. Полностью это научное направление сформировалось в исследованиях Г.Лейбница, Я.Бернулли и Л.Эйлера, В диссертации Г.Лейбница «Комбинаторное искусство» появился и закрепился сам термин «комбинаторный». Впрочем, отдельные элементы комбинаторики использовались еще в первой половине XVI века итальянским математиком Никколо Тарталья.
4. Задачи комбинаторики
Комбинаторикой или комбинаторным анализом называется раздел математики, посвященный решению задач выбора и расположения элементов некоторого дискретного множества в соответствии с заданным правилом.
Это правило определяет способ построения некоторой конструкции из элементов исходного множества, которая называется комбинаторной конфигурацией.
Основные задачи комбинаторики:
определение условий существования нужных конфигураций,
задание алгоритмов их построения,
оптимизация алгоритмов,
перечисление всех конфигураций.
Решать подобные задачи человеку приходится очень часто. Почти Ежедневно у себя дома он занимается комбинаторным анализом, даже не догадываясь об этом. Например, расставляя мебель в квартире, хозяин методом проб интуитивно решает задачу оптимального размещения в различных комнатах отдельных групп предметов из имеющегося мебельного набора.
Более сложные комбинаторные задачи приходится решать в различных областях проектной, конструкторской и производственной деятельности. Так проектируя промышленное, административное или жилое здание, проектировщик обязан в соответствии с техническим заданием оптимально по экономическим и функциональным критериям расположить все внутренние помещения, определить количество, размеры и положение оконных проемов, указать число, мощность и местоположение источников искусственного освещения и т.д.
2. Основные комбинаторные принципы (Андерсон, Джеймс а.)
Нам важнее нахождение и использование общих схем для подсчетов, чем решение отдельных задач. Наша цель – избегать простого перечисления элементов с последующим подсчетом, в особенности, если таких элементов очень много. Однако, данный метод можно использовать для небольшого количества объектов, если это поможет найти общую схему.
Представьте
себе, что человек, которому нечем больше
заняться, подбрасывает монету и кость
(в виде игрального кубика). На монете
может выпасть "орел" (H)
и "решка" (Т). При падении кости
возможные исходы представляют собой
1,
2, 3, 4, 5 и 6. Возможными исходами обоих
событий являются (Н, 1), (Н, 2), (Н, 3). (Н, 4),
(Н, 5), (Н, 6), (T,
1), (T,
2), (T,
3), (Т, 4). (Т, 5) и (Т, 6). Один из возможных
способов представить эти события –
построить дерево
подсчета, изображенное
на рис. 8.1.
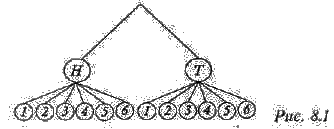
Для нахождения исхода (Н,2) идем по левой ветке к Н, а затем по ветке к 2. Очевидно, что таким образом представлены все исходы событий, и каждое из обведенных чисел изображает единственный исход. Если на монете выпал Н, то существуют шесть возможных исходов для кубика; и те же шесть возможных исходов, если выпала "решка" Т. Таким образом, можно найти общее количество исходов, умножая 2 х 6, т.е. умножая число возможных исходов для подбрасывания монеты на число возможных исходов для подбрасывания игральной кости. Следует обратить внимание, что исход подбрасывания монеты не влияет на возможный исход подбрасывания кости.
Аналогичным образом предположить, что выбирается сначала одна буква из 26-символьного алфавита, а затем – вторая, причем вторая буква может совпадать с первой. Для нахождения общего числа буквенных пар важно заметить, что имеются 26 вариантов выбора первой буквы, и для каждой выбранной первой буквы существуют 26 вариантов выбора второй. Следовательно, существуют 26 х 26 = 676 возможных способов выбора из алфавита буквенных пар. Если вторая буква не должна совпадать с первой, то после выбора первой буквы имеется только 25 вариантов выбора второй. Поэтому всего имеются 26 х 25 = 650 возможных вариантов выбора. Другой способ решения этой же задачи: вычесть из 676, общего числа возможных вариантов выбора буквенных пар из алфавита, число всех вариантов, в которых обе буквы совпадают. Их, понятно, 26, поэтому, вычитая 26 из 676, снова получаем 650.