Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

SalimovRB_matematika_gl_1-9_2011_web

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

3.69 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1911 12 13 14 15 16 17 18 19 > Следующая >>>

рому определению непрерывной функции lim V 0.	Подставив последние
x 0
три предела в (12), получим формулу (с) .Теорема доказана.
Следствие из утверждения ( b ) теоремы 3. Если c	– постоянная,V V (x)

–дифференцируемая функция, то (cV ) cV .

Всамом деле, когда U c const , имеем U c 0 , и формула ( b ) теоремы

2даёт c V c V c V c V .

§6. Производные тригонометрических и логарифмической

функций

Теоремы 4	и 5 (производные синуса и косинуса).		Если y sin x,	то
y cos x. Если	y cos x, то	y sin x. Или коротко	sin x cos x	и

cos x sin x.

Доказательство. Докажем первую теорему (вторая доказывается анало-

гично).
Производная функции			y f (x) sin x согласно			формуле (8)	равна
y lim sin(x x) sin x .		Числитель формулы справа можно разложить по из-
x 0	x
вестной	из тригонометрии		формуле	разности синусов: sin(x x) sin x
2sin( x / 2) cos(x x / 2).		Подставив это выражение в предыдущую формулу,
получим	y lim sin( x / 2) cos(x x / 2) .			Справа	предел	произведения	равен
	x 0	x / 2
произведению пределов, поэтому
			y lim sin( x / 2)		lim cos(x x / 2).		(13)
			x 0	x / 2	x 0

Но первый предел равен единице, т. к. представляет собой «первый замеча-

тельный предел», в котором x 2 0.			А второй предел, в силу непрерыв-
ности косинуса, при x 0 и x x / 2 x			равенcos x. Подставив эти пределы
в формулу (13), получим то, что требуется. Теорема доказана.
Теоремы 6 и 7 (производные тангенса и котангенса). Если y tg x,				то
y 1 cos2 x. Если	y ctg x, то	y 1 sin2	x. Или коротко: tg x 1 cos2 x	и
ctg x 1 sin2 x.

101

5354.ru

Доказательство. Докажем первую теорему (вторая доказывается аналогично). С учётом формулы ( c ) теоремы 3 имеем

cos

x sin

tg x

sin x

sin

x cos x sin x cos x

cos

cos x

Теорема 8 (производная логарифмической

функции).

Если y loga x,

то y 1 x ln a 1

x loga e. Или коротко: loga x

1/(x ln a) (loga e) / x.

Доказательство. Согласно определению производной

loga x lim

loga x x

loga x

x 0

В числителе воспользуемся тем, что разность логарифмов равна логарифму отношения, поэтому

loga x lim 1x loga 1 xx .

x 0

Выражение под знаком предела разделим и умножим на x, затем множитель 1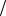 x вынесем за знак предела, так как он не зависит от x. Получим

x x

loga x

lim

loga 1

lim loga 1

x 0

x x

Так как логарифм – непрерывная функция, знаки предела и логарифма можно поменять местами, поэтому

	1				x x
loga x	x	loga lim	1		.

		x 0		x x

При фиксированном x 0 и x 0 имеем

реме 17 главы 4	lim	1 1/ x x	e.	Поэтому
	x 0
	x

x x x . Значит, согласно тео-loga x 1x loga e . Пришли к утвер-

ждению теоремы.

В частности, при a e имеем ln a ln e 1 и loga x loge x ln x. Тогда утверждение теоремы примет вид ln x 1/ x.

102

5354.ru

§ 7. Производная сложной функции

Теорема 9 (производная сложной функции). Если y		f U , а U x ,
т. е. y – сложная функция от x y f (x) , причём f U		и x	– диффе-
ренцируемые функции, то справедлива формула
yx f U U x	f U x		(14)
Доказательство. Приращению x аргумента	функции U x		отвечает

приращение U x x x , а последнему приращению аргумента U функции y f U отвечает приращение y f U U f U . Таким образом, приращению x аргумента x в конечном счёте отвечает приращение y рас-

сматриваемой сложной функции y,	зависящей от	x.	Поэтому производная
этой сложной функции будет равна
	yx lim	y .	(15)
	x 0	x
Учтём, что так как функция U x	является дифференцируемой, то, как бы-

ло доказано ранее, она является непрерывной, поэтому, согласно второму

определению непрерывности,			для функции U x	имеем lim U Иначе
				x 0
говоря, U 0,	если x 0. Теперь, умножив и поделив на U, запишем от-
	y	y	U
ношение y x	в виде x		x .
ношение y x	в виде x	U	x .
В этом соотношении перейдём к пределу при x 0				(при этом U 0 ), кро-

ме того, учтём, что предел правой части равен произведению пределов. В итоге получим

lim

U .

(16)

x 0

U 0

x 0

Так как функции y f U

и U f (x) являются дифференцируемыми, то су-

ществуют конечные пределы

(17)

lim

U ,

U 0

lim

x .

(18)

x 0

103

5354.ru

Согласно (16) из существования пределов (17) и (18) вытекает существование предела (15). Производные (15), (17) и (18) подставим в (16) вместо соответствующих пределов и придём к формуле (14). Теорема доказана.

	Например,	пусть дана сложная функция y cosU, U ln x, т. е.		y cos(ln x).
По	формуле	(14) имеем для производной	этой сложной	функции
yx	cosU u Ux	(sinU ) / x. Здесь U ln x, поэтому	yx [sin ln x ]/(x). Анало-

гично получается формула для дифференцирования сложной функции, состоящей из трёх и большего числа составляющих функций. Запишем формулу для дифференцирования сложной функции, состоящей из трех составляющих функций.

Пусть y f (U ), U (V ), V (x). Имеем сложную функцию y f { x ]}. Её производная будет равна

y x f U UV Vx f U (V ) ( x).

Коротко правило дифференцирования сложной функции можно записать так:

производная сложной функции равна произведению производных её составляющих по своим аргументам.

§ 8. Производные степенной и показательной функций. Логарифмическое дифференцирование

Теорема 10 (производная степенной функции). Если y xn , n 0 – лю-

бое действительное число, то y nxn 1 или коротко: (xn )x nxn 1.

Доказательство. Пусть x 0. От соотношения y xn , n 0 , возьмём натуральный логарифм: ln y n ln x. Далее продифференцируем эту функцию, при этом показатель степени n как постоянный множитель вынесем за знак про-

изводной: ln y x n ln x x . Отсюда

ln y x n / x.

(19)

Здесь производная левой части есть производная сложной функции. Так как логарифм зависит от y, который в свою очередь зависит от x , то по формуле

(14) имеем ln y x ln y y yx . Но ln y y 1 y , поэтому

ln y x	1	yx .	(20)
	y

104

5354.ru

Это выражение подставим в левую часть (19) и получим yx / y n / x или yx ny / x. Подставив сюда y xn , получим то, что требуется. Теорема доказана. При n 1 теорема дает (x)x 1.

Доказательство теоремы проведено для случая x 0. Без обоснования отметим, что утверждение теоремы справедливо и для x 0.

Замечание. При доказательстве теоремы соотношение y xn сначала прологарифмировали, взяв натуральный логарифм от него, а затем полученное соотношение продифференцировали по x. Операция взятия логарифма и последующего дифференцирования называется логарифмическим дифферен-

цированием, а выражение (20) называется логарифмической производной.

Теорема 11 (производная показательной функции). Если	y ax , то
y ax ln a. Или коротко: ax x ax ln a.
Доказательство теоремы аналогично предыдущему. При a e	теорема да-
ет (ex )x ex .

Наконец, отметим, что производные от степенно-показательных функций вида y [U x ]v x находятся с помощью логарифмического дифференцирования. Вычислим, например, производную функции y xx . Для этого прологарифмируем, а затем продифференцируем обе части равенства y xx . Получим

ln y ln xx или	ln y x ln x . Далее,	(ln y)'x (x ln x)'x . С учетом (20) имеем
yx' / y ( x ln x)'x ,	yx' y(1 ln x x(1/ x)). Отсюда yx' xx (ln x 1).

§ 9. Неявная функция и её производная

Функция y f x называется неявной, если она определена соотношени-

ем, не разрешенным относительно y :
F x, y 0,	(21)

где F x, y – известное выражение. Например, таковыми являются соотношения

x2 y2 1 0 ,	(22)
xy 1 ey 0 .	(23)
Если соотношение (21) удаётся разрешить относительно	y, то мы придём к

явному заданию. Например, из (22) следует y 1 x2 . Но такой переход не

105

5354.ru

y x2

x ( y)

y x2

x y ,

всегда возможен, например, в случае функции, заданной уравнением (23). Однако всегда можно найти производную неявной функции. Для этого достаточно соотношение (21) продифференцировать по x, помня, что в нём y есть

функция от x.

Сделаем это применительно к функции, определённой неявно

формулой (23). Соотношение (23) продифференцируем по

учитывая, что

слагаемое xy

– произведение двух функций, а слагаемое ey

– сложная функ-

ция. Получим 1 y x yx ey yx 0. Отсюда найдем искомую производную

yx y /( x ey ).

(24)

В этой формуле y

– значение функции, соответствующее взятому x , согласно

(23). В частности, из соотношения (23) видно, что значению

x 0

отвечает

значение y 0, т. к. при этих значениях соотношение (23)

выполняется. По-

этому

при

x 0

производная yx , согласно (24),

будет

равна

x 0

y 0

x e

x 0

§ 10. Обратная функция и ее производная

Пусть дана функция y f x . Выразим из этого соотношения x через y и получим где y – аргумент, а x – функция. Эта последняя функция называется обратной к функции y f x . Ясно, что на плоскости Oxy этим

функциям отвечает один график, так как они представляют собой разные формы записи одной и той же зависимости. Например, для функции обратной является x y. Здесь каждому значению y отвечают два значения x. В этом случае говорят, что функция x y является многозначной. В данном случае она двузначна. Ясно, что из этой двузначной функции можно получить две однозначные функции, а именно, x y и x y. Эти одно-

значные функции называются ветвями рассматриваемой многозначной функции. В дальнейшем всегда в случае многозначной обратной функции под обратной функцией будем понимать какую-либо выбранную нами однозначную её ветвь. Например, для функции в качестве обрат-

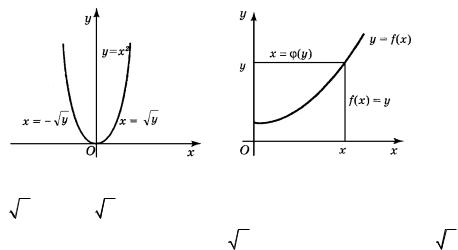
ной можно взять либо x y , либо x y по нашему усмотрению. Функции отвечает парабола (рис. 49).

106

5354.ru

	Рис. 49
Функциям x y и x	y отвечают соответственно правая и левая части
параболы, для которых x 0	(в случае x	y ) и x 0 (в случае x y ).

Отметим следующий геометрически очевидный факт: если график функции y f x является восходящей (нисходящей) кривой, т. е. с увеличением

абсциссы x точки кривой её ордината y f x увеличивается (уменьшается), то обратная к ней функция x ( y) существует и будет однозначной, так как каждому значению y из области значений функции y f x отвечает лишь одно значение x обратной функции x ( y).

В предыдущем примере для функции y x2 это условие нарушается, так как кривая y x2 состоит из двух частей: одна является нисходящей, а другая

восходящей.
Теорема 12 (о производной обратной функции). Если			x ( y) – функ-
ция, обратная по отношению к функции			то
	y f x , и ( y) 0,
		y	(25)
	f ( x) 1/
или коротко: yx 1/ xy .
Доказательство. Соотношение x ( y) определяет функцию, обратную к

y f	x , поэтому x f x Полученное соотношение продифференцируем
по x,	помня, что в правой части стоит сложная функция. Тогда будем иметь
1 y yx . Отсюда yx 1/ y или yx 1/ xy .

§ 11. Производные обратных тригонометрических функций

Функция y Arcsin x является обратной по отношению к функции x sin y. График функции x sin y совпадает с графиком функции y Arcsin x . Для любого x из интервала 1 x 1 на графике функции y Arcsin x (рис. 50) имеется бесчисленное множество точек с абсциссой x, их ординаты – значения функции. Следовательно, эта функция является бесконечнозначной. Возьмём ту

107

5354.ru

часть графика, где 2 y 2 ; на этом участке для каждого x из интервала [ 1; 1] имеется лишь одна точка с абсциссой x. В дальнейшем под функцией

y Arcsin x

всегда будем понимать ветвь функции, значения которой лежат в

интервале / 2 y / 2

и обозначать её y arcsinx .

Теорема 13.

Если

y arcsin x,

то

y 1

1 x2

или

коротко:

arcsin x 1/

1 x2 .

Доказательство.

Производная функции

x sin y

равна

xy cos y. Так как

функция y arcsin x – обратная к x sin y, то согласно (25) имеем

yx 1/ cos y.

(26)

Мы нашли искомую производ-

ную, но пока она выражена че-

рез y, а не через x. Но x sin y,

следовательно,

cos y

нужно

выразить через sin y x.

Как из-

вестно,

cos y

1 sin2

но

функция

y arcsin x принимает

значения

из

интервала

2 y 2. Для таких y,

как

мы

знаем,

cos y 0,

следова-

Рис. 51

Рис. 50

тельно, в предыдущей формуле

мы должны оставить знак «+». Таким образом, cos y

1 sin2

y . Так как

sin y x, то cos y

1 x2 . Подставив это выражение в (26), получим утвержде-

ние теоремы 13.

Функция

y Arccos x

– обратная по отношению к функции x cos y (см.

Рис. 52

Рис. 53

108

5354.ru

рис. 51) В дальнейшем всегда под функцией y arccos x будем понимать одно-

значную ветвь	функции	y Arccos x ,	значения которой лежат в		интервале
0 y . Для этой функции справедлива следующая
Теорема 14.	Если	y arccos x ,	то yx 1	1 x2 или	коротко:

(arccos x)x 1/

1 x2 .

Доказательство проводится аналогично предыдущему.

Функция y Arc tg x является обратной по отношению к функции x tg y

(см. рис. 52). Выберем её однозначную ветвь, для которой				2 y 2. В
дальнейшем эту ветвь будем обозначать y arctg x . Для нее справедлива
Теорема 15. Если	y arctg x, то	yx 1 1 x2	или	коротко:

arc tg x x 1/(1 x2 ).

Доказательство проводится по аналогии с доказательством теоремы 13. Функция y Arcc tg x является обратной по отношению к функции x ctg y . Выберем её однозначную ветвь, значения которой лежат в интервале 0 y

(рис. 53). Обозначим эту ветвь y arcctg x. Для этой функции справедлива

Теорема 16. Если y arcctg x, то yx 1 1 x2 или коротко:

arcctg x x 1/(1 x2 ).

Доказательство проводится по той же схеме, что и в случае теоремы 13.

§12. Функция, заданная параметрически,

иее дифференцирование

Даны две дифференцируемые функции

x t , y t . (27)

Аргумент t будем называть параметром, пусть он изменяется в интервале

	t .
	На плоскости Oxy возьмём точку M , коорди-
	наты x,	y кото-рой вычисляются	по формуле
	(27). Если t изменяется, то изменяются и коорди-
	наты x,	y , и точка M опи-сывает некоторую ли-
	нию (см. рис. 54). В этом случае соот-ношения
Рис. 54	(27) называют парамет-рическими		уравнениями
указанной линии. Из первого уравнения (27) выразим t через			x и получим

109

5354.ru

функцию t x , обратную к функции x (t). Это выражение для t подста-

вим во второе уравнение (27) вместо t	и тогда получим
	y x	(28)
Таким образом, оказывается, что y	зависит от x, т. е.	y является функци-

ей от x. К этой функции мы пришли, исходя из формул (27), следовательно,

эти формулы определяют функцию y от x. Функция,
определяемая из (27), называется параметрически
заданной, а задание её с помощью этих формул
называется параметрическим заданием функции.
В качестве примеров приведем параметрические
уравнения окружности и эллипса.
На плоскости Oxy возьмём окружность радиуса r
с центром в начале координат, M x; y – произволь-	Рис. 55
		изме-
ная точка окружности (рис. 55). Вектор OM образует с осью Ox угол t,		изме-

ряемый в радианах. Этот угол счи-тается положительным, если он отсчитывается против хода часовой стрелки от оси Ox . Из рис. 55 видно, что

x r cos t, y r sin t.

Эти соотношения представляют собой параметрические уравнения окружности, так как при изменении t в интервале 0 t 2 точка M описывает полную окружность.

Теперь возьмем на плоскости Oxy эллипс с уравнением

x2 / a2 y2 / b2 1.	(29)
Уравнения
x a cost, y bsin t,0 t 2 ,	(30)

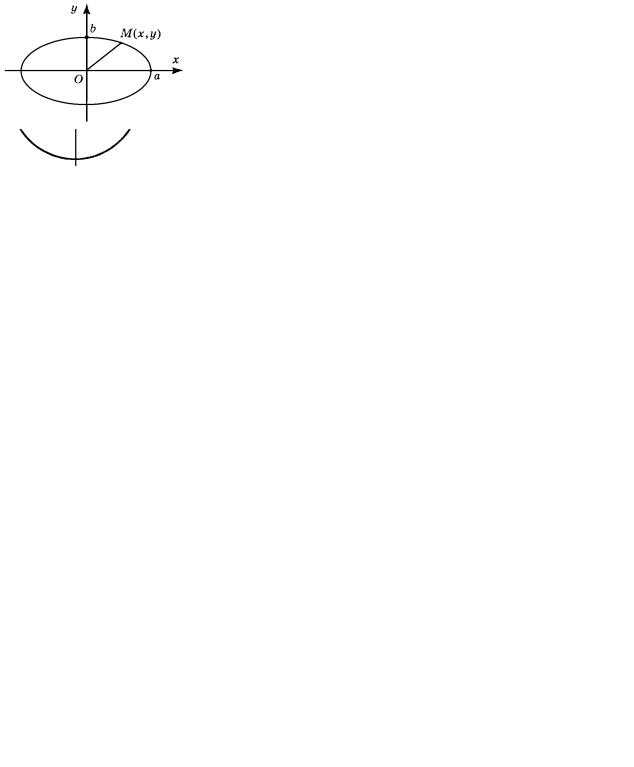
представляют собой параметрические уравнения указанного эллипса. В самом деле, точка M x; y , координаты которой вычисляются по формулам

(30), лежит на эллипсе, так как её координаты (30) удовлетворяют уравнению эллипса (29). Кроме того, точка M при изменении t в указанном интервале описывает полный эллипс

(рис. 56).

Выведем теперь формулу для производной yx функции y от x, определяемой формулами (27).

Рис. 56 Про-дифференцируем по x соотношение (28) и

110

5354.ru

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1911 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.05.2015371.27 Кб10rulturologiy 2.pdf
#
14.11.2018293.89 Кб4russkij-yaz.-egye-chast-s-yenciklopediya.doc
#
17.03.2016150.23 Кб9rutrvar56.pdf
#
17.03.2016311.15 Кб4ryady_metod_ukazaniya_kgasu_5354.pdf
#
12.05.20153.88 Mб42SalimovRB_matematika_gl_1-20_2011_web.pdf
#
12.05.20153.69 Mб71SalimovRB_matematika_gl_1-9_2011_web.pdf
#
11.05.2015988.67 Кб44Sbornik_testov_s_otvetami_marketing.doc
#
12.05.20159.79 Mб13SGH_i900_service_manual-spaces_ru.pdf
#
12.05.2015526.35 Кб48Shavali_Burova_109_13.pdf
#
11.05.2015710.66 Кб23Shpargalka_po_pravookhranitelnym_organam.doc
#
27.09.2019520.19 Кб15shpora1.doc