
SalimovRB_matematika_gl_1-9_2011_web
.pdf
исследуем эту точку с помощью достаточного признака экстремума: при x 0 имеем f x 2x 0, при x 0 имеем f x 2x 0, т. е. f x
изменяет знак с «-» на «+», поэтому x 0 есть точка минимума функции
fx ;
находим минимальное значение функции f 0 0.
Если критическая точка является точкой разрыва функции f x и в ней
функция обращается в бесконечность, то эта критическая точка не будет точкой экстремума функции, если даже при переходе через неё изменяется знак производной f x . Например, для функции
f x 1/ x2 |
точка x 0 |
является критической |
|
точкой, |
так как |
в ней производная |
|
f x 2 / x3 не существует. Знак этой произ- |
|
||
водной изменяется с «+» на «-». При этом |
|
||
точка x 0 не является точкой максимума, |
|
||
так как в |
ней функция имеет разрыв: при |
|
|
x 0 f x . График этой функции пока- |
Рис. 67 |
||
зан на рис. 67. |
|
|
|
Теорема 5 (второй достаточный признак экстремума функции). Пусть
x0 – критическая точка дважды дифференцируемой функции f x , |
т. е. |
f x0 0. Тогда, если f x0 0, то x0 является точкой экстремума f |
x , а |
именно, точкой максимума при f x0 0 и точкой минимума при f x0 0. |
|
Доказательство. Докажем теорему для случая, когда f x0 0. Нужно |
|
показать в этом случае, что критическая точка x0 – точка минимума. При до-
казательстве дополнительно предположим, что |
f x |
непрерывна в точке x0 . |
|||||||||||
Это означает, что lim f x f x0 . |
|
|
|
|
|
|
|
|
|
|
|||
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
Возьмём число , |
равное f x0 / 2. |
Это число положительное согласно |
|||||||||||
условию. Для этого числа согласно определению предела функции |
f x |
при |
|||||||||||
x x0 найдётся |
такое число |
, |
что |
для |
всех точек |
интервала |
|||||||
x0 x x0 |
будет выполняться неравенство |
|
f x f x0 |
|
f x0 / 2 |
или |
|||||||
|
|
||||||||||||
равносильное |
ему |
неравенство |
f x0 / 2 |
|
f x f x0 f x0 / 2, |
т. е. |
|||||||
f x0 / 2 f x |
3 f x0 / 2. Итак, для всех |
x |
из интервала x0 x x0 |
||||||||||
131
5354.ru

выполняется неравенство 0 f x0 / 2 f x . Значит, f x 0 |
или f x 0. |
Отсюда ясно, что в указанном интервале производная f x |
возрастает, так |
как её производная f x f x 0 . Поэтому большему значению аргумента
x отвечают |
большие значения |
функции: f x f x0 0 при |
x x0 , |
||
f x |
f x0 0 |
при x x0. Итак, знак f x изменяется с «-» на «+» при пере- |
|||
ходе x |
через |
x0 |
с увеличением x. |
Согласно первому достаточному признаку |
|
экстремума приходим к выводу, что x0 – точка минимума. Вторая часть теоремы доказывается аналогично.
Пример 2. Найдём экстремум функции |
y sin x в |
интервале |
0 x . |
|||
Здесь |
f x sin x, |
f x cos x, |
f x sin x. |
При исследовании |
функции |
|
y sin x воспользуемся вышеуказанной схемой: |
|
|
|
|||
|
f x cos x обращается в нуль только в точке x |
2 интервала 0 x |
||||
|
; |
|
|
|
|
|
|
исследуем эту точку с помощью второго достаточного признака экс- |
|||||
|
тремума, здесь f 2 sin 2 1 0 ; следовательно, x 2 |
– точка |
||||
|
максимума; |
|
|
|
|
|
|
находим максимальное значение f 2 sin 2 1. |
|
|
|||
Рассмотрим одну из задач на нахождение наибольшего значения функции в интервале.
Дан квадратный жестяной лист со стороной a. По углам листа вырезают одинаковые квадраты и, сгибая лист по линиям выреза, образуют коробку. Какова должна быть длина x сторон вырезанных квадратов, чтобы объём V коробки был наибольшим?
Основанием коробки служит квадрат со стороной a 2x, высота коробки равна x, поэтому объём коробки равен
V a 2x 2 x. |
(2) |
Ясно, что в (2) аргумент x изменяется в интервале 0 x a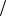 2. Нужно найти точку, в которой функция принимает наибольшее значение в этом интервале. На концах интервала, т. е. при x 0 и x a
2. Нужно найти точку, в которой функция принимает наибольшее значение в этом интервале. На концах интервала, т. е. при x 0 и x a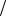 2 , функция (2) обращается в нуль, а внутри интервала принимает положительные значения. Следовательно, наибольшее значение функция принимает внутри интервала 0, a
2 , функция (2) обращается в нуль, а внутри интервала принимает положительные значения. Следовательно, наибольшее значение функция принимает внутри интервала 0, a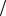 2 . Найдём в этом интервале точки максимума рассматриваемой функции. Производная
2 . Найдём в этом интервале точки максимума рассматриваемой функции. Производная
132
5354.ru

Vx a 2x a 6x этой функции обращается в нуль в единственной точке x a / 6 интервала  Ясно, что она является точкой максимума функции
Ясно, что она является точкой максимума функции
(2), в которой эта функция принимает наибольшее значение в интервале0, a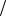 2 .Таким образом, получен ответ: x a / 6.
2 .Таким образом, получен ответ: x a / 6.
§ 4. Выпуклость линии. Точки перегиба кривой
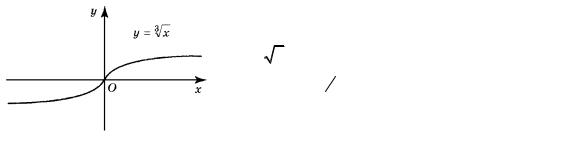
Кривая |
y f x называется выпуклой вверх в |
|
интервале a, b , если она лежит ниже любой сво- |
||
ей касательной в точках, абсциссы которых лежат |
||
в этом интервале (см. рис. 68). |
|
|
Кривая |
y f x называется |
выпуклой вниз |
(вогнутой) |
в интервале a, b , |
если она лежит |
выше любой своей касательной в точках, абсцис- |
Рис. 68 |
|
|
сы которых лежат в этом интервале (см. рис. 69). |
|
Точка кривой, отделяющая выпуклую вверх |
|
часть от выпуклой вниз, называется точкой пере- |
ги- |
ба. Ясно, что касательная к кривой в точке пере- |
гиба |
пересекает кривую, т. к. выпуклая вверх часть ле- |
жит |
ниже касательной, а выпуклая вниз – выше каса- |
|
тельной (см. рис. 70). |
|
Здесь и далее будем считать, что функция |
Рис. 69 |
y f (x) дважды дифференцируема всюду в обла- |
|
сти определения. |
|
Известно, что вычисленная в точке x производная |
f x равна тангенсу |
угла , образованного с осью Ox касательной к кривой в её точке с абсцис- |
|
сой x. Для выпуклой вверх кривой (см. рис. 68) с увеличением x угол убывает, следовательно,
убывает |
f x tg , |
значит, |
производная |
|
f x f x 0 согласно необходимому |
при- |
|||
знаку убывания функции. Аналогично убедимся |
||||
в том, что если кривая |
y f x |
выпуклая вниз, |
||
то f x 0. Итак, пришли к теореме. |
Рис. 70 |
|||
133
5354.ru
Теорема 6 (необходимые признаки выпуклости кривой). Если кривая y f x является выпуклой вверх на a, b , то в этом интервале f x 0 ; ес-
ли кривая y f x является выпуклой вниз на a, b , то в этом интервале
f x 0.
Теорема 7 (достаточные признаки выпуклости кривой). Если f x 0
всюду |
в интервале |
a, b , то в этом интервале |
кривая y f x выпуклая |
вверх. |
Если f x 0 |
всюду в интервале a, b , то |
в этом интервале кривая |
y f x выпуклая вниз.
Доказательство. Докажем первую часть теоремы. Пусть f x 0 всюду в интервале a, b . Тогда, согласно достаточному признаку убывания функ-
ции, в этом интервале f x |
убывает с увеличением x. Значит, |
f x tg |
убывает всюду в интервале |
a, b . Следовательно, кривая y f x |
является |
выпуклой вверх, что очевидно геометрически. Теорема доказана. |
|
|
Теорема 8 (необходимый признак точки перегиба). Если x0 – абсцисса точки перегиба кривой y f x , то f x0 0.
Доказательство. Точка перегиба отделяет выпуклую вверх часть от выпуклой вниз, следовательно, она одновременно принадлежит обеим указанным частям кривой. Будем считать, что вторая производная существует
и непрерывна в точке x0 . Для выпуклой вверх части кривой y f x , согласно
необходимому |
признаку |
выпуклости |
кривой, |
f x 0, |
поэтому |
||
lim f x f x0 0. |
Для выпуклой вниз части кривой |
y f x , согласно не- |
|||||
x x0 |
|
|
|
|
|
|
|
обходимому |
|
признаку |
выпуклости |
кривой, |
f x 0, |
поэтому |
|
lim f x f x0 0. |
Но эти два соотношения должны выполняться одновре- |
||||||
x x0 |
|
|
|
|
|
|
|
менно, следовательно, f x0 0. Теорема доказана. |
|
|
|||||
Абсциссой точки перегиба может служить и |
|
|
|||||
значение x0 , |
при котором f x не существует. |
|
|
||||
Покажем это на примере кривой y 3 x. |
Здесь |
|
|
||||
f (x) 3 x, |
f x (1/ 3) x 2 3 , |
f x (2 / 9) x 53 . |
|
|
|||
Отметим, что |
при |
x 0 |
вторая производная |
|
|
||
f x не существует, т. е. не существует |
f 0 . |
Рис. 71 |
|
||||
|
|
|
|
|
|
|
|
134
5354.ru

Кроме того, видим, что f x 0 при x 0 , а при x 0 имеем f x 0. Зна-
чит, по теореме 7 при x 0 кривая выпуклая вниз, при x 0 - выпуклая вверх. Это означает, что x 0 есть абсцисса точки перегиба рассматриваемой кривой. Это также очевидно из графика функции (см. рис. 71).
Теорема 9 (достаточный признак точки перегиба). Точка(x0 , y0 ) кривой y f (x) является точкой перегиба, если f (x) обращается в нуль или не существует при x x0 и знак второй производной f x изменяется при переходе x через x0 (с увеличением x ). При перемене знака с «-» на «+» участок
выпуклости вверх сменяется участком выпуклости вниз, а при перемене с «+» на «-» участок выпуклости вниз сменяется участком выпуклости вверх.
Доказательство. Пусть знак f x |
изменяется с «-» на «+» при переходе |
|
x через x0 |
с увеличением x, т. е. при x x0 имеем f x 0, а при x x0 полу- |
|
чим f x |
0. Тогда, согласно достаточному признаку выпуклости кривой, |
|
слева от x0 |
лежит участок выпуклости вверх кривой, а справа от x0 – участок |
|
выпуклости вниз. Следовательно, x0 |
– абсцисса точки перегиба кривой |
|
y f x . Вторая часть теоремы доказывается аналогично. Для нахождения точек перегиба кривой y f x требуется:
найти точки, в которых f x обращается в нуль или не существует;
каждую такую точку исследовать с помощью достаточного признака точки перегиба;
найти ординаты точек перегиба, подставив их абсциссы в выражение y f x вместо x.
Пример. Найти точку перегиба линии y x3. Здесь |
f x x3 , |
f x 3x2 , |
|
f x 6x. Далее, |
|
|
|
производная f x 6x существует всюду и обра- |
|
|
|
щается в нуль в единственной точке x 0 ; |
|
|
|
исследуем точку x 0 с помощью |
достаточного |
|
|
признака точки перегиба: при x 0 имеем |
f x 6x 0, а |
|
|
при |
x 0 |
f x 6x 0, т. е. знак «-» изменяется на «+», |
|
||
следовательно, x 0 есть абсцисса точки перегиба; |
|
Рис. 72 |
|||
|
найдём ординату точки перегиба, подставив |
x 0 в |
|||
|
|||||
135
5354.ru

уравнение кривой, получим y 0.
Итак, точкой перегиба кривой является точка 0; 0 . Эта кривая имеет график, представленный на рис. 72.
§ 5. Асимптоты кривой
Прямая называется асимптотой кривой, если расстояние от точки этой кривой до прямой стремится к нулю, когда указанная точка неограниченно удаляется от начала координат. Рассмотрим два вида асимптот.
Вертикальные асимптоты. Дана кривая с урав- |
||||||||||||||
нением y |
|
|
|
|
|
x x |
|
|
|
|
|
|
0 |
– заданное |
f |
|
x |
|
. Если lim |
f |
|
x |
|
, |
x |
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
число, то кривая имеет вертикальную асимптоту с |
||||||||||||||
уравнением |
|
x x0 . |
Здесь |
график |
функции будет |
|||||||||
иметь вид, указанный, например, на рис. 73. |
||||||||||||||
На кривой |
|
y f x возьмём точку M с абсцис- |
||||||||||||
сой x и ординатой |
f x . Пусть точка N |
– основание |
||||||||||||
перпендикуляра, опущенного из точки |
Рис. 73 |
|||||||||||||
M на пря- |
||||||||||||||
мую x x0 . Тогда расстоя-ние от точки M до прямой с уравнением x x0 рав-
но MN x x0 . |
|
|
По условию |
при x x0 , когда |
x x0 MN стремится к нулю, имеем |
f x , а точка |
M кривой неограниченно удаляется от начал координат. |
|
Иначе говоря, когда точка M неограниченно удаляется от начала координат, |
||
расстояние MN стремится к нулю. Это значит, что прямая с уравнением x x0 есть асимптота линии y f x .
Наклонные |
асимптоты. |
Пусть |
кривая |
|
||
y f x имеет наклонную асимптоту с уравнени- |
|
|||||
ем y kx b, |
где k |
– угловой коэффициент асимп- |
|
|||
тоты, т. е. |
k tg |
угол образован с осью Ox |
|
|||
асимптотой (рис. 74). На кривой |
y f x |
возьмём |
|
|||
точку M с координатами x, y , |
y f ( x). |
На пря- |
|
|||
мой y kx b (асимптоте рассматриваемой кривой) |
Рис. 74 |
|||||
возьмём точку M1 |
с той же абсциссой, |
что и у |
||||
|
||||||
точки M . Её ордината равна kx b. Поэтому
136
5354.ru

MM1 f x kx b . |
(3) |
Так как мы рассматриваем наклонную асимптоту, то считаем, что угол не равен 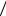 2. Это означает, что cos Пусть точка N – основание перпендикуляра, опущен-ного из точки M на асимптоту. Получили прямоугольный треуголь-ник NMM1 . Из него найдем выражение MN MM1 cos поэтому, учитывая, что cos , будем иметь
2. Это означает, что cos Пусть точка N – основание перпендикуляра, опущен-ного из точки M на асимптоту. Получили прямоугольный треуголь-ник NMM1 . Из него найдем выражение MN MM1 cos поэтому, учитывая, что cos , будем иметь
|
MM1 NM / cos . |
(4) |
|
Прямая y kx b |
есть асимптота линии y f x , |
следовательно, расстоя- |
|
ние MN от точки M до прямой стремится к нулю, когда точка M неограни- |
|||
ченно удаляется от |
начала координат, т. е. её абсцисса x стремится к беско- |
||
нечности. |
|
|
|
Итак, MN 0 при x , значит, согласно (4) |
MM1 0 при x , |
т. е. |
|
lim MM1 0. Подставим сюда вместо MM1 выражение (3) и получим |
|
||
x |
|
|
|
|
lim f x kx b 0. |
(5) |
|
|
x |
|
|
Из (5) видно, что выражение под знаком предела – бесконечно малая функ-
ция, которую |
обозначим |
через p(x) . Тогда p( x) f x kx b |
или |
f (x) kx b p(x), |
где p(x) |
при x . Это соотношение поделим на x, |
пе- |
рейдем к пределу при x и учтем, что предел суммы есть сумма пределов. Получим
|
|
|
lim |
f x |
lim k lim b |
lim |
p(x) |
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x |
|
x |
x x |
|
x |
|
x |
|
|
|
|
|
|
|
|
|||||||
Поскольку 1 x 0 при |
x , |
|
произведение постоянной b на 1 x есть беско- |
||||||||||||||||||||||
нечно малая величина, а её предел равен нулю. Аналогично |
lim( p(x) / x) 0. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
Предел постоянной k |
равен k, |
поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k lim[ f x / x]. |
|
|
(6) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||
Соотношение (5) запишем так: |
lim |
f x kx b |
0. |
Учтём, что слева предел |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разности равен разности пределов и |
limb b. |
Поэтому |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
f |
|
x |
|
kx |
|
lim b 0, lim |
|
f |
|
x |
|
kx |
|
b 0, |
|
|
|
|||||||
x |
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b lim |
f |
|
x |
|
kx |
|
. |
(7) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||
137
5354.ru
Итак, мы показали, что если линия y f x имеет наклонную асимптоту y kx b, то обязательно существуют два конечных предела (6) и (7) для чисел k и b, входящих в уравнение асимптоты. И наоборот, если для линии y f x существуют два конечных предела (6), (7), то эта линия имеет наклонную асимптоту y kx b. В этом можно убедиться, проведя изложен-
ные выше рассуждения в обратном порядке. |
|
Пример. Возьмём кривую с уравнением y f x , где |
f x x2 /(1 x). Эта |
кривая имеет вертикальную асимптоту с уравнением x 1. В самом деле,
lim[x2 /(1 x)] .
x 1
Найдём наклонную асимптоту этой линии. Вычислим сначала предел (6): |
|||||
k lim |
f x |
lim |
x |
. Последний предел найдём по правилу Лопиталя, так как |
|
x |
1 x |
||||
x |
x |
|
|||
здесь и числитель, и знаменатель стремятся к бесконечности. Получим
lim |
x |
lim |
x |
lim1 1. |
Итак, |
k 1. Теперь найдём предел (7): |
|||||||
1 x |
1 x |
||||||||||||
x |
x |
x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
f x kx |
|
x2 |
|
|
x |
|||
|
|
|
b lim |
lim |
|
x |
1 lim |
|
. |
||||
|
|
|
1 x |
|
|||||||||
|
|
|
|
x |
|
|
x |
|
x |
1 x |
|||
Последний предел равен 1, следовательно, b 1. Зная k и b , запишем уравнение наклонной асимптоты y x 1.
§6. Общая схема исследования функций
ипостроения графиков
Общая схема исследования функции y f x заключается в следующем:
находим область определения функции и ее точки разрыва;отыскиваем сначала критические точки, в которых производная
обращается в нуль или не существует; затем находим интервалы возрастания
и убывания функции, в которых f x сохраняет знак, |
точки максимума и |
минимума, максимальное и минимальное ее значения; |
|
определяем точки, в которых вторая производная |
f x обращается в |
нуль или не существует, затем находим интервалы выпуклости вверх и вы-
пуклости вниз функции f x , в которых |
f x сохраняет знак, и точки пере- |
гиба; |
|
138
5354.ru
отыскиваем асимптоты кривой.
При построении графика целесообразно сначала изобразить асимптоты. Пример. Исследуем функцию y f (x) x2 /(1 x) . Имеем
f x x x 2 1 x 2 , f x 2 1 x 3 . Далее следуем вышеуказанной схеме.
Функция определена всюду, кроме точки x 1, |
которая является точкой |
||
разрыва, и f x при |
x 1. Областью определения является совокуп- |
||
ность интервалов ; 1 , |
1; . |
Производная f x обращается в нуль в |
|
точках x 2 и x 0 и не существует в точке x 1. |
Итак, критическими точ- |
||
ками являются x1 2, x2 1, x3 0. |
Ими определяются интервалы возраста- |
||
ния и убывания функции: |
; 2 , |
2; 1 , 1; 0 , |
0; . На них соответ- |
ственно f x 0, f x 0, |
f x 0, |
f x 0, т. е. |
f x сначала возрастает, |
потом убывает, опять убывает и снова возрастает. Точка x1 2 является точкой максимума, так как знак первой производной изменяется с «+» на «-»; ymax f x x 2 4. Точка x2 1 не является точкой
экстремума, так как она – точка разрыва функции. Точка x3 0 – точка минимума функции f x , так как при переходе через неё первая производная изменяет знак с «-» на «+», и ymin f x x 0 0.
Вторая производная f x не существует в точке |
|
|
x 1; на интервале ; 1 |
она отрицательна, зна- |
|
чит, кривая выпукла вверх, |
а на интервале 1; |
|
кривая выпукла вниз, так как здесь f x 0. Точка |
|
|
x 1 не является абсциссой точки перегиба, по- |
|
|
скольку функция в этой точке не определена. Кри- |
|
|
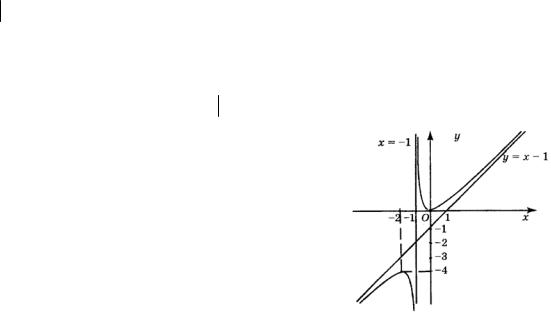
вая имеет асимптоты: вертикальную x 1 и наклон- |
Рис. 75 |
|
ную y x 1. График исследуемой функции пред- |
||
ставлен на рис. 75.
139
5354.ru
ГЛАВА 8. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ
§ 1. Производная длины дуги кривой
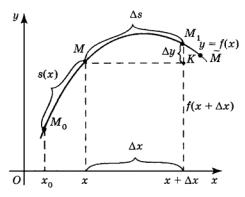
Пусть в плоскости Oxy задана кривая y f x (рис. 76), точка M 0 с абсциссой x0 – фиксированная точка кривой, а точка M с абсциссой x – переменная точка. Введём понятие длины дуги части M0 M заданной кривой. Дугу
M0M
разделим на n частей точками M1, M2 , ... , Mn 1. Каждые две соседние точки, включая M0 , M , соединим хордой и получим ломаную M0 M1M2 ... M , соеди-няющую точки M 0 и M и состоящую из n звеньев. Длину ломаной обозначим через ln. Число n всех звеньев устре-
мим к бесконечности так, чтобы длины звеньев стремились к нулю. При этом вышеуказанная ломаная по форме будет приближаться к дуге
Рис. 76 |
|
|
Поэтому за длину дуги кривой M0 M |
есте- |
|
M0M. |
|||
ственно принять |
s lim ln . |
Так как M – переменная точка с абсциссой x, |
то с |
|
|
n |
|
|
|
изменением положения точки M (с изменением абсциссы x этой точки) дли-
на дуги s |
изменяется. Следовательно, эта дуга есть функция от x |
– абсциссы |
||||||
точки M . |
Обозначим ее s s x . |
|
|
|
|
|
|
|
На кривой возьмём точку M1 с абсциссой x x. |
На рис. 76 показан слу- |
|||||||
чай, когда x 0. |
Длина дуги кривой |
|
получается из функции s x |
заме- |
||||
M0M1 |
||||||||
ной x на x x, |
т. е. заменой абсциссы x |
точки M на абсциссу |
x x |
точки |
||||
M1. |
|
|
|
|
|
|
|
|
Итак, |
длина дуги кривой |
|
есть |
s x x . Длина |
дуги |
|||
M0M1 |
||||||||
|
|
|
|
|
|
s x в точке |
x, соответ- |
|
MM1 s x x s x s – это приращение функции |
||||||||
ствующее приращению x. Поэтому |
|
|
|
|
|
|
||
|
|
|
|
lim |
s s x . |
|
(1) |
|
|
|
|
|
x 0 |
x |
|
|
|
140
5354.ru
