SalimovRB_matematika_gl_1-9_2011_web

(18) отвечает вектор r , конец M которого лежит на прямой. При изменении t

Как известно, при умножении вектора на число умножаются на это число все проекции вектора на оси координат, поэтому ta tm,tn,tp . При сложении

Эти соотношения называют параметрическими уравнениями рассматривае-

мой прямой. Каждому значению параметра t на прямой отвечает определённая точка M , координаты x, y, z которой вычисляются по формуле (19). При

изменении t точка M с указанными координатами движется по прямой, и её координаты изменяются согласно (19).

§ 6. Канонические уравнения прямой. Уравнения прямой, проходящей через две заданные точки

Из каждого уравнения в (19) выразим t , полученные выражения приравняем и тогда будем иметь

Эти соотношения называют каноническими уравнениями рассматриваемой прямой; здесь – заданные координаты точки M0 прямой; x, y, z – текущие координаты, т. е. координаты произвольной точки M прямой; m, n, p – заданные числа, равные проекциям на оси координат направляющего вектора a прямой. Из формулы (20) можно получить уравнения

31

5354.ru

Ясно, что каждое из них, как уравнение первой степени относительно текущих координат в пространстве Oxyz, определяет плоскость. Пересекаясь, эти плоскости определяют рассматриваемую прямую. Соотношение (20) исполь-

случае числители дробей, знаменатели которых равны нулю, мы также будем считать равными нулю, т. е. x x0 0, y y0 0 . Эти два уравнения определя-

ют рассматриваемую прямую, причём каждое из них определяет плоскость, а прямая является линией их пересечения.

Уравнения прямой, проходящей через две заданные точки. Даны две точки M1 x1, y1, z1 , M 2 x2 , y2 , z2 , лежащие на прямой. Координаты этих точек

заданные числа. Нужно записать уравнения прямой, проходящей через эти

две точки.

Вектор M1M2 x2 x1, y2 y1, z2 z1 лежит на рассматриваемой прямой, по-

этому его можно взять в качестве ее направляющего вектора. В качестве начальной точки прямой можно взять любую из указанных точек, например, M1 . Тогда уравнения (20) запишутся так:

§ 7. Угол между двумя прямыми, условия параллельности и перпендикулярности

Пусть в пространстве Oxyz две прямые заданы уравнениями

32

5354.ru

§ 9. Общее уравнение прямой на плоскости, угол между прямыми

Мы знаем, что уравнение первой степени

(26)

в пространстве Oxyz определяет плоскость, параллельную оси Oz, причём её нормальный вектор N A, B, 0 . Пусть эта плоскость пересекается с плоскостью Oxy по прямой PQ (рис. 21) и M x, y, 0 – произвольная точка этой пря-

мой. Так как точка M лежит на плоскости с уравнением (26), то координаты этой точки в пространстве удовлетворяют этому уравнению. Таким образом, координаты x, y произвольной точки M прямой PQ удовлетворяют (26). Следовательно, это и есть уравнение указанной прямой PQ .

Итак, уравнение (26) в пространстве Oxyz определяет плоскость, параллельную оси Oz. Это же уравнение на плоскости Oxy определяет прямую, являющуюся линией пересечения указанной плоскости с плоскостью Oxy .

Уравнение (26) называется общим уравнением прямой на плоскости.

В дальнейшем у точки M этой прямой и у нормального вектора N этой прямой третьи нулевые координаты записывать не будем. Прямую будем изображать в плоскости Oxy (рис. 22).

ра N прямой на оси координат. По аналогии с общим уравнением плоскости можно рассмотреть частные случаи общего уравнения прямой, когда те или иные коэффициенты этого уравнения обращаются в нуль.

Пусть на плоскости Oxy две прямые заданы уравнениями

34

5354.ru

Условие параллельности прямых. Если A1 / A2 B1 / B2 , то прямые (27),

(28) параллельны, так как коллинеарны их нормальные векторы. С учётом формулы (29) записанное выше условие параллельности прямых можно представить в виде k1 k2 .

Условие перпендикулярности прямых. Если имеет место равенство

A1 A2 B1B2 0 , то прямые (27) и (28) перпендикулярны. С учётом формулы (29) условие перпендикулярности прямых запишем так: k1 1/ k2 .

§ 11. Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом.

Уравнение прямой, проходящей через две заданные точки

Пусть дана точка M1 x1, y1 , лежащая на прямой, и известен угловой коэф-

фициент k этой прямой. Нужно записать ее уравнение.

Так как эта прямая проходит через точку M1 x1, y1 , то ее координаты удовлетворяют уравнению (30), т. е. y1 kx1 b . Полученное соотношение вычтем из (30) и придем к уравнению прямой, проходящей через точку M1 x1, y1 :

Пусть теперь даны две точки M1 x1, y1 и M 2 x2 , y2 . Нужно записать урав-

нение прямой, проходящей через них. Здесь можем воспользоваться уравнением (31). Величина k пока не известна. Учтём, что прямая проходит также через точку M2 , поэтому координаты этой точки должны удовлетворять

уравнению (31), т. е. y2 y1 k x2 x1 . Исключим k из последних двух урав-

нений. Для этого нужно соотношение (31) почленно поделить на последнее. Получим искомое уравнение ( y y1 ) /( y2 y1 ) (x x1 ) /(x2 x1 ).

§ 12. Кривые второго порядка. Окружность

Кривой второго порядка называется линия на плоскости Oxy, определяемая уравнением второй степени относительно текущих координат x , y вида

36

5354.ru

менно не обращаются в нуль, поскольку в противном случае (32) обращается в уравнение первой степени.

Рассмотрим отдельные случаи уравнения (32) и соответствующие им кривые.

Окружность. Как мы уже знаем, окружность радиуса R с центром в точ-

В уравнении (34) коэффициенты при квадратах текущих координат равны друг другу. Кроме того, в этом уравнении отсутствует член, содержащий произведение текущих координат. Легко проверить, что если в уравнении (32) A C , B 0 , то оно будет определять окружность в плоскости Oxy (если уравнению отвечает множество точек). Чтобы убедиться в сказанном, достаточно уравнение (32) поделить на A C , после чего в левой части выделить полные

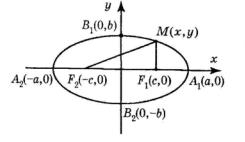
§ 13. Эллипс

определению эллипса сумма расстояний от любой точки эллипса до фокусов равна 2a , т. е.

37

5354.ru

Из треугольника F1MF2 видно, что 2a 2c . Запишем расстояния через координаты:

F1M x c 2 y 0 2 , F2 M x c 2 y 0 2 . (36)

Эти выражения подставим в (35) и получим

x c 2 y2 x c 2 y2 2a .

Последнему соотношению удовлетворяют координаты любой точки эллипса, следовательно, это соотношение – уравнение эллипса. Нужно его упростить. Второй корень перенесём из левой части вправо и возведём обе части уравнения в квадрат. Тогда будем иметь

x c 2 y2 2 2a x c 2 y2 2 ,

x2 2xc c2 y2 4a2 4a x c 2 y2 x2 2xc c2 y2 .

После приведения подобных членов в правой части оставим корень с множителем, остальные слагаемые перенесём влево и полученное выражение возведём в квадрат. Обозначим b2 a2 c2 (так как a c ), считая b 0. После простых преобразований получим соотношение

Такое уравнение эллипса называется каноническим. Имея уравнение (37), выясним форму эллипса.

Пусть M x, y – произвольная точка эллипса. На плоскости Oxy возьмём точку M ' x, y , имеющую ту же абсциссу x , что и точка М, а ординату y ,

отличающуюся от ординаты точки М только знаком. Точка M ' симметрична M относительно оси Ox. Уравнение (37) содержит y только во второй степе-

ни и y 2 y2 . Точка M x, y лежит на эллипсе, поэтому её координаты удо-

влетворяют уравнению эллипса, но тогда этому уравнению удовлетворяют координаты точки M ' , так как абсцисса точки М равна абсциссе M , а ординаты различаются лишь знаком. Получаем, что точка M лежит на эллипсе, но сказанное относится к произвольной точке M эллипса, следовательно, эллипс будет симметричным относительно оси Ox. Так как в (37) x содержится

38

5354.ru

только в квадрате, рассуждая аналогично, покажем, что ось Oy также является осью симметрии эллипса, следовательно, начало координат O – центр симметрии эллипса. В силу симметрии форму эллипса достаточно выяснить для

Получили выражение для ординаты y точки M эллипса с абсциссой x. Когда абсцисса точки M принимает значение x 0 , то согласно (38) ее ордината y b . Точка M находится на Oy в точкеB1 0,b . С увеличением абсциссы точки M ордината этой точки согласно (38) уменьшается. Точка M опускается и

§ 14. Гипербола

Знак «+» берётся, когда левая часть положительна, а знак «-» – когда левая часть отрицательна. Расстояния F1M и F2 M , как и раньше, выражаются формулами (36). Подставим (36) в (39):

39

5354.ru

Получили уравнение гиперболы. Как видно из рис. 25, 2c есть длина стороны F1F2 треугольника F1F2 M , и она больше 2a , поэтому b2 c2 a2 , b – действи-

тельное число, которое будем считать положительным. Уравнение (40) упростим, убрав корни так же, как в уравнении эллипса. Получим каноническое уравнение гиперболы

Исследуем форму гиперболы, исходя из уравнения (41) (как и в случае эллипса). Так как (41) содержит x и y только во второй степени, то Ox и Oy являются осями симметрии гиперболы (аналогично случаю эллипса), поэтому точка пересечения этих осей – начало координат – центр симметрии

гиперболы. Ясно, что для установления вида гиперболы достаточно рассмотреть картину в первой четверти плоскости, где x 0 и y 0 . Для таких значе-

40

5354.ru