
SalimovRB_matematika_gl_1-9_2011_web
.pdf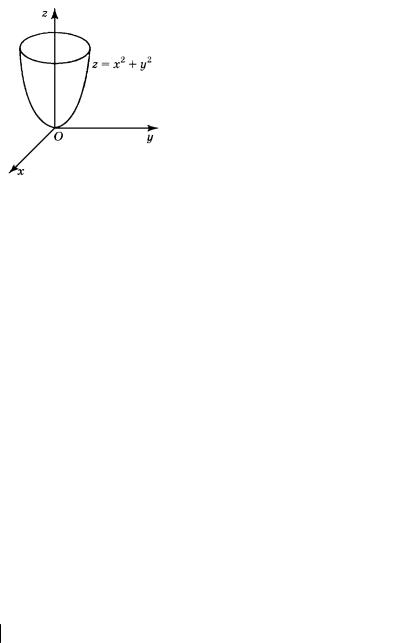
дном, обращенным вниз. Например, 0, 0 |
– точка |
|
|
|
||||
минимума функции z x2 y2 . В самом деле, значение |
|
|
|
|||||
функции в этой точке меньше её значений в любой |
|
|
|
|||||
другой точке x, y . График этой функции представ- |
|
|
|
|||||
лен на рис. 95. |
|
|
|
|
|
|
|
|
Точки максимума и минимума называются |
|
|
|
|||||
точками экстремума функции, а значения функции в |
|
|
|
|||||
них – экстремальными значениями (минимальными и |
|
Рис. 95 |
|
|||||
максимальными). |
|
|
|
|
|
|
|
|
Теорема 3. Если x0 , y0 – точка экстремума функции |
z f x, |
y , то в |
||||||
этой точке производные f (x, y) |
|
, |
f (x, y) |
|
равны нулю или не суще- |
|||
|
|
|||||||
x |
x x0 |
|
y |
x x0 |
|
|
|
|
|
y y0 |
|
|
y y |
|
|
|
|
ствуют. |
|
|
|
0 |
|
|
|
|
|
x0 , y0 есть |
|
|
|
|
|||
Доказательство. Дано, что |
точка |
экстремума |
функции |
|||||
z f x, y . Это означает, что при фиксированном |
y y0 |
z f |
x, y0 – функция |
|||||
одного переменного x – в точке x x0 имеет экстремум. Следовательно, согласно необходимому признаку экстремума функции одной переменной, про-
изводная |
zx fx x, y0 в |
точке x x0 равна нулю или не существует. |
Однако |
|||||
последняя |
производная |
является |
частной производной |
по x |
от функции |
|||
z f x, y , |
так как y y0 . Итак, |
z / x f x, y0 / x при |
x x0 |
обращается в |
||||
нуль или не существует, следовательно, частная производная |
f x, |
y / x |
|
x x0 |
||||
|
||||||||
|
|
|
|
|
|
|
|
y y0 |
обращается в нуль или не существует. Аналогично можно показать, что част-
ная производная f x, y / y x x0 равна нулю или не существует.
y y0
Пример. Функция z f x, y x2 |
y2 |
имеет минимум в начале координат и |
её частные производные f x, y / x |
2x, |
f x, y / y 2 y обращаются в нуль в |
точке 0, 0 .
Точки, в которых обе частные производные функции z f (x, y) обращаются в нуль или не существуют, называются критическими точками. Согласно предыдущей теореме точка экстремума функции z f (x, y) является ее критической точкой. В то же время не всякая критическая точка является точкой экстремума.
171
5354.ru
Например, |
для функции z f x, y x2 |
y2 |
имеем f x, y / x 2x, |
f x, y / y 2 y. |
Обе эти производные в точке |
0, 0 |
обращаются в нуль, но |
она не является точкой экстремума рассматриваемой функции. В самом деле, эта функция в точке 0, 0 принимает значение, равное нулю. Но это значение
не является ни максимальным, ни минимальным, так как для всех точек оси Ox, для которых y 0, функция принима-ет значения
z x2 0, а для всех точек оси Oy, для которых x 0, |
|
|
функция принимает значения z y2 0. |
Иначе гово- |
|
ря, рассматриваемая функция вблизи |
точки 0, 0 |
|
принимает значения как большие, так и меньшие ну- |
|
|
ля. Поэтому её значение в точке 0, 0 , равное нулю, |
|
|
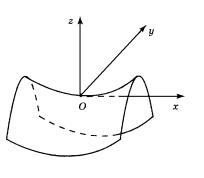
не является ни максимальным, ни минимальным. Это |
Рис. 96 |
|
очевидно геометрически, так как график рассматриваемой функции является гиперболическим параболоидом (рис. 96).
На вопрос, будет ли критическая точка точкой экстремума, отвечает достаточный признак экстремума функции двух переменных z f x, y .
§ 15. Достаточный признак экстремума Схема исследования на экстремум функции двух переменных
Теорема 4. Пусть x0 , y0 |
– критическая точка функции z f x, y , когда |
|||||||||||||||||
f (x, y) |
|
0, |
f (x, y) |
|
0. |
Обозначим |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||||
x |
|
|
x x0 |
y |
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y0 |
|
|
y y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
2 f x, y |
|
|
, B |
2 f x, y |
|
, C |
2 f x, y |
|
. |
||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
x y |
|
y2 |
|
|||||
|
|
|
|
|
|
|
|
x x |
|
|
|
x x |
|
x x |
||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
Тогда: |
|
|
|
|
|
|
|
|
y y0 |
|
|
|
|
y y0 |
|
|
y y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
если AC B2 |
0, |
то x0 , |
y0 есть точка экстремума функции z f x, y , |
||||||||||||||
причём точка максимума при A 0 |
и точка минимума при A 0; |
|||||||||||||||||
|
если AC B2 |
0, |
то x0 , |
y0 не является точкой экстремума. |
||||||||||||||
|
если AC B2 0, то требуются дополнительные исследования. |
|||||||||||||||||
Теорема принимается без доказательства.
Из изложенного вытекает следующая схема исследования функции z f x, y на экстремум:
172
5354.ru
найти критические точки этой функции (т. е. точки x0 , y0 , в которых
первые частные производные функции обращаются в нуль или не существуют); каждую найденную критическую точку исследовать с помощью доста-
точного признака экстремума; |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
найти экстремальные значения функции z f (x, y) , подставив вместо x |
|||||||||||||||||
и y |
координаты точки максимума или минимума. |
|
|
|
||||||||||||||
|
Пример. |
Исследуем |
|
на |
|
экстремум |
|
функцию z f (x, y), где |
||||||||||
f x, y x3 y3 3xy. Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
z |
3x |
2 |
3y, |
z |
3y |
2 |
3x, |
2 z |
|
6x, |
|
2 z |
3, |
2 z |
6 y. |
||
|
x |
|
y |
|
x2 |
|
x y |
y2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Поступим согласно указанной выше схеме. |
|
|
|
|
|
|
|
|||||||||||
Найдем критические точки функции: |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
3y 0, |
|
|
|
2 |
y 0, |
|
|
||||
|
|
|
|
|
3x |
|
|
|
x |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0. |
|
|
||
|
|
|
|
|
3y2 3x 0, |
|
|
y2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получили систему двух уравнений с двумя неизвестными для нахождения координат критических точек. Из второго уравнения выразим x y2 и подста-
вим в первое уравнение. Тогда или Приравняв
нулю первый, а затем второй множители (третий множитель в нуль не обращается), получим два корня: y1 0 и y2 1. Этим двум значениям отвечают соответствующие значения x1 0 и x2 1. Итак, получили две критические
точки 0; 0 и 1; 1 .
С помощью достаточного признака экстремума нужно исследовать каждую из этих критических точек. Исследуем сначала вторую точку 1; 1 .
Здесь имеем
A |
2 |
f x, y |
|
|
|
|
6x |
|
|
6, B |
|
2 f x, y |
|
3, |
||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
x2 |
|
|
|
x 1 |
|
x 1 |
|
x y |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
||||||
|
|
|
|
|
|
y |
1 |
|
|
|
|
|
|
|
|
|
|
|
y 1 |
|
|
|
|
C |
|
2 f x, y |
|
6 y |
|
|
6. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
y2 |
|
|
|
|
y 1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 1 |
|
|
|
|
|
|
Таким образом, AC B2 27 0, |
следовательно, точка 1;1 – точка экстремума, |
|||||||||||||||||||
а именно, точка минимума, так как A 6 0 . |
|
|
|
|
|
|
||||||||||||||
5354.ru |
173 |
|

Найдём теперь минимальное значение функции в точке |
1; 1 . Подставим |
||
координаты этой точки в выражение для функции z x3 y3 |
3xy и получим |
||
zmin z |
|
x 1 13 13 3 1. |
|
|
|
||
|
|
y 1 |
|
Другая критическая точка (0,0) исследуется аналогично. Она не является точкой экстремума.
§ 16. Нахождение наибольшего и наименьшего значений функции двух переменных в замкнутой области
Пусть в конечной области D с границей L плоскости Oxy задана непрерывная функция z f x, y и найдены значения функции в ее критических точках, лежащих в области D. Эти значения обозначим z1, z2 , ..., zn . Аналогич-
но случаю функции одного аргумента рассматриваемая функция своё наибольшее и наименьшее значения в области D может принять в точках её границы L. Поэтому при нахождении указанных значений надо рассматривать также значения функции в точках границы L области D и среди последних выделить наибольшее и наименьшее значения, которые обозначим соот-
ветственно M L , mL . С учетом теоремы 1 § 6 настоящей главы заключаем, что наибольшее значение функции z f x, y в замкнутой области D будет равно наибольшему из чисел z1, z2 , ..., zn , M L , а наименьшее значение – наименьшему
из чисел z1, z2 , ..., zn , mL .
Нахождение значений ML и mL сводится к отысканию наибольшего и наименьшего значений функции одного аргумента.
|
|
|
|
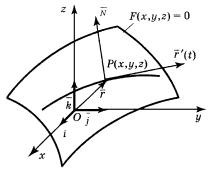
Проиллюстрируем сказанное на примере области D, |
||||||||||||||
|
|
|
|
граница L которой состоит из двух частей L1 |
и L2 , за- |
|||||||||||||
|
|
|
|
данных |
соответственно |
уравнениями |
|
y x , |
||||||||||
|
|
|
|
a x b, |
и x y , |
c y d, где x , |
x |
– одно- |
||||||||||
|
|
|
|
значные непрерывные функции (см. рис. 97). Здесь |
||||||||||||||
Рис. 97 |
|
|
|
(a) c, (b) d, |
c a, d b. Так как |
y |
x есть |
|||||||||||
|
|
|
ордината точки с абсциссой x кривой L1, значения |
|||||||||||||||
|
|
|
|
|||||||||||||||
функции f x, |
y |
|
на L1 |
представляют собой значения функции одного аргу- |
||||||||||||||
|
|
|
|
b. Аналогично значения функции f |
|
|
|
|
|
2 |
||||||||
мента f x, x |
, |
a x |
|
x, |
y |
|
на L есть |
|||||||||||
значения функции аргумента |
y : |
f y |
, y , |
c |
|
y |
|
d. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
174
5354.ru

Пусть |
M L |
и mL |
– соответственно наибольшее и наименьшее значения |
|||
|
1 |
1 |
|
|
|
|
функции |
f x, x |
в интервале a x b, а |
M L |
и mL |
– соответственно |
|
|
|
|
|
2 |
2 |
|
наибольшее и наименьшее значения функции |
f y , y в интервале c y d. |
|||||
|
|
|
|
|
|
|
Эти числа находятся известным нам способом (§ 2 главы 7). Ясно, что mL есть наименьшее из чисел mL1 , mL2 , а ML – наибольшее из чисел M L1 и M L2 .
Аналогично поступаем в случае, когда кривую L можно разбить на части указанного вида, число которых больше двух.
Пример. Требуется найти наибольшее и наименьшее значения функции z x2 y2 в круге, ограниченном окружностью x2 y2 1.
Как уже отмечалось, эта функция, график которой изображен на рис. 96, не имеет экстремумов, так как ее единственная критическая точка (0,0) не яв-
ляется точкой экстремума (см. § 14). Следовательно, наибольшее и наименьшее значения она принимает в точках границы –
окружности x2 y2 1. |
Последнее уравнение запишем в виде |
|
y |
1 x2 при y 0; |
y 1 x2 при y 0. |
Эти уравнения определяют две полуокружности, из которых состоит исход-
ная окружность. В точках первой полуокружности ( y 0) |
функция z x2 y2 |
|
принимает значения z x2 (1 x2 ), т. е. z 2x2 1, |
1 x 1. |
Такие же значения |
эта функция принимает в точках второй полуокружности. Следовательно, достаточно найти наибольшее и наименьшее значения функции z 2x2 1 в интервале 1 x 1. Ее производная z 4x обращается в нуль при x 0, это единственная критическая точка рассматриваемой функции в интервале [ 1,1]. Она является точкой минимума согласно теореме 5 § 3 главы 7, так как z 4 0. Минимальное значение функции равно z |x 0 1. Ясно, что значения функции z 2x2 1 на концах интервала [ 1,1], равные 1, являются ее наибольшими значениями. Итак, наибольшее и наименьшие значения функции z x2 y2 в круге x2 y2 1 равны соответственно 1 и 1.
§ 17. Касательная плоскость и нормаль к поверхности
Прямая называется касательной к поверхности в точке P x, y, z этой по-
верхности, если указанная прямая является касательной в точке P к какойлибо линии, лежащей на поверхности и проходящей через точку P. Так как
175
5354.ru
через точку P проходит бесчисленное множество линий, лежащих на поверхности, то ясно, что касательных прямых к поверхности в точке P бесчисленное множество. В связи с этим докажем следующее утверждение.
Теорема 5. Пусть в пространстве Oxyz поверхность задана уравнением
F(x, y, z) 0 |
(39) |
и точка P с координатами x, y, z этой поверхности такова, что вычисленные в ней частные производные F / x, F / y, F / z от левой части уравне-
ния (39) не обращаются в нуль одновременно. Тогда все касательные прямые к поверхности в точке P лежат в одной плоскости.
Доказательство. Пусть поверхность, задан- |
|
|
ная уравнением (39), имеет вид, указанный на |
|
|
рис. 98. Пусть L – произвольная линия, лежащая |
|
|
на поверхности и проходящая через ее точку |
|
|
P x, y, z . Параметрические уравнения этой ли- |
Рис. 98 |
|
нии запишем так: |
||
|
||
x x t , |
y y t , z z t . (40) |
(здесь t – параметр). От параметрических уравнений L перейдём к векторному уравнению r r(t), где r xi y j zk,
|
r t x t |
i y t j z t k. |
(41) |
Здесь r r(t) |
– радиус-вектор точки P x, y, z . |
Мы знаем, что производная от |
|
функции (41), r t x t i y t j z t k, вычисленная для точки P, |
отвечаю- |
||
щей выбранному значе-нию параметра t, есть вектор с началом в точке P, направленный по касательной к линии L. Будем считать, что кривая L вы-
брана так, что r t 0. С другой стороны, вычислим частные производные от левой части уравнения (39) для точки P. Построим вектор N с началом в точ-
ке P, |
проекции на оси координат которого равны этим частным производ- |
||||
ным: |
N F / x, F / y, F / z . По условию теоремы проекции этого вектора |
||||
не обращаются в нуль одновременно, следовательно, длина вектора |
|
N |
|
0. Но |
|
|
|
||||
кривая L лежит на поверхности, поэтому координаты любой её точки, определённые по формулам (40), удовлетворяют уравнению (39), т. е. для всех t F x t , y t , z t 0. Это соотношение продифференцируем по t , учитывая,
176
5354.ru
что левая часть – сложная функция, в которой F – функция трёх переменных. Поэтому
|
|
|
|
|
|
|
|
F |
xt F yt |
F zt |
0. |
(42) |
|
|
|
|
|
|
|
|
x |
y |
z |
|
|
Соотношение (42) справедливо для любой точки линии L и в том числе для |
||||||||||||
значения t, отвечающего точке P. |
Возьмём скалярное произведение векторов |
|||||||||||
N и r t , |
построенных в точке P. |
Оно равно сумме произведений одноимён- |
||||||||||
ных |
проекций |
|
соответствующих |
векторов |
N |
и |
r (t) : |
|||||
|
|
F |
|
F |
|
F |
|
В силу (42) правая часть последней форму- |
||||
N, r |
(t) |
x |
x (t) |
y |
y (t) |
z |
z (t). |
|||||
|
|
|
|
|
|
|
|
|
|
|||
лы равна нулю. Итак, скалярное произведение (N , r (t)) 0, а поскольку длины
векторов не равны нулю - векторы перпендикулярны. Итак, N r t , |
но L – |
любая кривая, лежащая на поверхности и проходящая через точку P. |
Таким |
образом, любая касательная прямая к поверхности перпендикулярна векторуN. Это означает, что все касательные прямые к поверхности в точке P перпендикулярны N – одному и тому же вектору. Следовательно, все касательные прямые лежат в одной плоскости. Теорема доказана.
Указанная плоскость называется касательной плоскостью к поверхности в точке P. Мы показали, что вектор N с началом в точке P, проекции которого F / x, F / y, F / z суть частные производные, вычисленные в точке P,
есть вектор, перпендикулярный к касательной плоскости поверхности в точке P, т. е. является нормальным вектором этой плоскости.
Прямая, проходящая через точку P и перпендикулярная к касательной плоскости в ней, называется нормалью к поверхности в точке P.
§18. Уравнение касательной плоскости и нормали
кповерхности
Пусть поверхность задана уравнением (39) и P0 x0 , y0 , z0 – фиксированная точка этой поверхности, т. е. её координаты x0 , y0 , z0 – заданные числа. Вычислим частные производные F x , F
x , F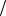 y , F
y , F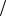 z и найдём их значения в точке
z и найдём их значения в точке
P0 :
177
5354.ru
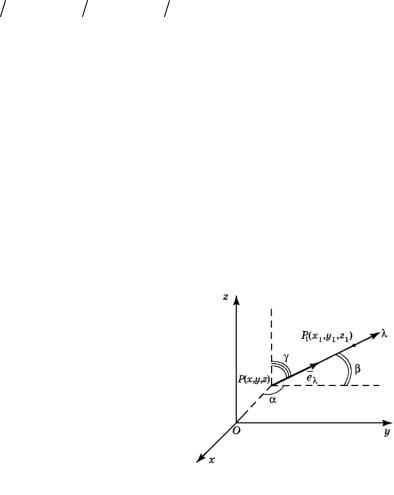
|
F |
|
F |
|
|
|
|
F |
|
|
F |
|
|
|
|
F |
|
F |
|
x x . |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
x x |
, |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
x P |
|
x |
|
y y0 |
|
|
y |
P |
|
y |
x x0 |
|
|
z P |
|
z |
|
y y0 |
|
|
0 |
|
0 |
|
|
|
|
|
y y |
|
|
0 |
|
0 |
||||||
|
|
|
|
|
z z0 |
|
|
|
0 |
|
|
z z |
0 |
|
|
|
|
|
|
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Получили определённые числа, которые являются проекциями нормального
вектора |
|
|
F |
|
|
F |
|
F |
|
|
|
касательной плоскости к поверхности в |
||||||||||
N |
|
|
|
, |
|
|
|
, |
|
|
|
|
||||||||||
|
|
|
x |
P |
|
y |
|
z |
P |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
P0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
||
точке P0 . |
Зная проекции этого вектора и координаты x0 , y0 , z0 |
точки P0 , сразу |
||||||||||||||||||||
запишем уравнение касательной плоскости: |
|
|
|
|
||||||||||||||||||
|
|
|
|
F |
x x |
|
F |
y y |
|
F |
z z 0. |
|
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
x P0 |
|
|
|
y P |
|
|
z P0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Зная координаты точки P |
и проекции вектора N |
для точки P , являющегося |
||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
направляющим вектором нормали к поверхности в точке P0 , |
запишем кано- |
|||||||||||||||||||||
нические уравнения этой нормали |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
y y0 |
|
|
z z0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||
|
|
|
|
|
|
|
F x P |
F y P |
F z P |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
В качестве примера возьмём сферу с центром в начале координат и урав-
нением x2 y2 |
z2 3 0. В точке P 1, 1, 1 сферы запишем уравнение касатель- |
|||||||||||||
ной плоскости и уравнение нормали. Итак, x0 1, |
|
y0 1, |
z0 1. |
|
||||||||||
|
F |
2x |
|
|
F |
|
|
|
|
F |
2z |
|
|
2. |
|
|
|
|
|
|
|||||||||
|
|
|
x x0 2, |
|
2 y |
|
y y0 2, |
|
|
|
z z0 |
|||
|
|
|
||||||||||||
|
|
|
|
|||||||||||
|
x P |
|
|
|
y |
P |
|
z P |
|
|
|
|
||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Решение данной задачи до конца предлагается довести самостоятельно.
§ 19. Производная по направлению
Пусть в системе координат Oxyz задано скалярное поле, т. е. функция трёх переменных U P U x, y, z , и P x, y, z – произвольная точка пространства. Проведем через нее ось , направ-
ление которой определяется единичным векто- |
|||
ром e (см. рис. 99). Пусть ось |
образует с ося- |
||
ми координат Ox, |
Oy, Oz углы |
, |
соответ- |
ственно, тогда |
e cos cos , cos . |
Пусть |
|
P1 x1 , y1 , z1 – произвольная точка оси , а расстояние
Рис. 99
PP1 Проекции векто-
178
5354.ru

ра PP1 на оси координат равны разностям координат конца и начала этого вектора:
|
(x1 x, y1 y, z1 z). |
(43) |
PP1 |
С другой стороны, проекции этого вектора равны его длине умноженной
на |
косинус |
угла между |
соответствующей осью и |
вектором, |
поэтому |
|
cos |
cos , cos . |
Последние проекции равны соответствующим |
||
PP1 |
|||||
проекциям в (43). Таким образом, |
|
|
|||
|
|
|
x1 cos x, y1 cos y, |
z1 cos z. |
(44) |
Следовательно, с учётом (44) имеем |
|
|
|||
|
|
|
U (P1 ) U (x cos , y cos , z cos ). |
(45) |
|
|
Пусть P |
– фиксированная точка, x, y, z – заданные числа и – фиксиро- |
|||
ванная ось, т. е. , – фиксированные величины. Пусть изменяется только
и точка |
P1 перемещается по оси относительно фиксированной точки P. |
|||||||||||||
При этом, как видно из формулы (45), значение U в точке P1 зависит только |
||||||||||||||
от одной переменной , следовательно, |
отношение [U P1 U P ]/ зависит |
|||||||||||||
только от одной переменной Предел этого отношения при |
0 (когда |
|||||||||||||
P1 P |
по |
оси ) называется производной по направлению |
|
от функции |
||||||||||
U P |
|
U x, y, z в точке |
P |
и обозначается |
U / |
|
U |
x, y, z . |
Итак, производ- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ная по направлению |
|
|
|
|
U P1 U P |
|
|
|
||||||
|
|
|
|
|
U |
lim |
. |
|
(46) |
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
Мы знаем, что для полного приращения функции трёх переменных справедливо представление
Ux x, y y, z z U x, y, z
U x U y U z 1 x 2 y 3 z,x y z
где 1, 2 , 3 – бесконечно малые функции, стремящиеся к нулю, когда x 0,y 0, z 0 одновременно. Это представление получено в предположении,
что частные производные U x , U y , |
U z непрерывны. В последней |
формуле положим x cos , y cos , |
z cos . Тогда |
179
5354.ru
|
U (x cos , y cos , z cos ) U (x, y, z) U |
cos |
|
||||
|
|
|
|
|
x |
|
|
|
U cos |
U cos 1 cos 2 cos 3 cos . |
|
||||
|
y |
z |
|
|
|
|
|
Левая часть этой формулы равна U P1 U P . |
Таким образом, получили вы- |
||||||
ражение для U P1 U P . |
Подставим его в числитель формулы (46) и сокра- |
||||||
тим на . |
При этом под знаком предела величины 1, 2 , |
3 стремятся к нулю |
|||||
при 0 |
(когда x 0, |
y 0, |
z 0 одновременно). Тогда (46) даст фор- |
||||
мулу для вычисления производной по направлению в точке P : |
|
||||||
|
|
U |
|
U |
U |
U |
(47) |
|
|
U x, y, z |
x |
cos y cos z cos . |
|||
|
|
|
|
|
|
|
|
Из неё видно, что эта производная зависит от:
координат x, y, z точки P, так как эти координаты входят в выражения для частных производных правой части формулы (47);
направления оси , т. е. от углов , , так как они входят в правую
часть формулы (47).
При фиксированных P и производная по направлению dU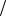 характеризует поведение функции при движении по оси . Когда dU
характеризует поведение функции при движении по оси . Когда dU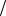 0, в положительном направлении оси функция U возрастает, причём тем быстрее, чем больше эта производная. В сказанном легко убедиться на основании (46).
0, в положительном направлении оси функция U возрастает, причём тем быстрее, чем больше эта производная. В сказанном легко убедиться на основании (46).
§20. Градиент функции и его связь
спроизводной по направлению
Пусть в пространстве Oxyz задано скалярное поле, т. е. функция U P U x, y, z , где x, y, z – координаты точки P. От этой функции найдём частные производные U x , U
x , U 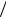 y , U
y , U 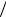 z. Эти производные вычислим для точки P x, y, z и построим вектор с началом в точке P, обозначаемый gradU
z. Эти производные вычислим для точки P x, y, z и построим вектор с началом в точке P, обозначаемый gradU
и называемый градиентом функции в точке P, проекции которого равны только что вычисленным частным производным. Итак, градиент функции U x, y, z в точке P равен
gradU |
U |
|
|
U |
|
U |
|
(48) |
x |
i |
y |
j |
z |
k. |
|||
|
|
|
|
|
|
Длина этого вектора определяется формулой
180
5354.ru
