
ТЕСТЫ по математике
.pdfМинистерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта ГОУ ВПО «Дальневосточный государственный университет путей сообщения»
Кафедра «Прикладная математика»
Е.П. Суляндзига, Г.А. Ушакова
ТЕСТЫ ПО МАТЕМАТИКЕ:
ПРЕДЕЛ, ПРОИЗВОДНАЯ, ЭЛЕМЕНТЫ АЛГЕБРЫ И ГЕОМЕТРИИ
Учебное пособие
Хабаровск Издательство ДВГУПС 2009
3
ВВЕДЕНИЕ
Всякое человеческое познание начинается с созерцаний, переходит от них к понятиям и заканчивается идеями.
И. Кант, “Критика чистого разума”
Предлагаемое учебное пособие можно рассматривать как сборник задач. Задачи охватывают традиционные темы – основы математического анализа: функцию, ее предел и производную. Присутствуют задачи по основам линейной алгебры и аналитической геометрии. Поскольку предел и производная функции являются более трудными, и кроме того, эти темы являются фундаментальными для интегрального исчисления, то им уделено наибольшее внимание: подробно разобраны решения типовых задач.
Теория пределов − это введение в теорию дифференцирования функции. Авторы надеются, что с помощью вербального аппарата им удалось рассказать о неопределенностях и правилах их раскрытия.
При нахождении производной сложной функции слишком трудно дается студентам установление порядка следования функций, образующих сложную функцию. Несомненно, этот материал надо увидеть в устном изложении преподавателя. Хочется верить, что при вдумчивом подходе читатель сможет самостоятельно разобраться и с дифференцированием сложной функции.
Собранный в учебном пособии материал неоднократно использовался на практических занятиях.
4
Repetitio est mater studiorum (лат.)
Повторение – мать обучения
Я занимался до сих пор решением ряда задач, ибо при изучении наук примеры полезнее правил.
И. Ньютон. “Всеобщая арифметика”
1.ПРЕДЕЛ. НЕОПРЕДЕЛЕННОСТИ И ПРАВИЛА ИХ РАСКРЫТИЯ
Функция α(x) называется бесконечно малой при x , стремящемся к некоторой заданной величине a : x → a , если предел α (x) при указанном
стремлении переменной x есть ноль: lim α (x) = 0.
x→a
Функция β(х) называется бесконечно большой при x , стремящемся
кнекоторой величине a , если при неограниченном приближении аргумента x к величине a абсолютные значения функции β(х) становятся и остаются гораздо большими как угодно большого наперед заданного
числа. Говорят, что в этом случае пределом функции β(х) является
бесконечность, и обозначается этот факт как lim β (x) = ∞ .
x→a
Бесконечно малая и бесконечно большая функции находятся в обратной зависимости:
1) если α(x) бесконечно малая функция при x → a , lim α (x) = 0,
x→a
то |
|
|
1 |
бесконечно большая функция при x → a : lim |
|
1 |
|
= ∞; |
|
α |
(x) |
|
|
|
|||||
|
x→aα (x) |
|
|||||||
|
2) если β(х) бесконечно большая функция при x → a , |
lim β (x)= ∞ , |
|||||||
|
|
|
|
|
|
|
x→a |
||
то |
|
|
1 |
бесконечно малая функция при x → a : lim |
|
1 |
|
= 0. |
|
|
β |
(x) |
|
|
|
||||
|
|
x→a β (x) |
|
|
|||||
Известно, что сумма и произведение бесконечно больших функций при стремлении аргумента x к некоторому фиксированному наперед
заданному значению |
a есть |
бесконечно большие функции. Теперь, |
||||
следуя |
|
|
|
|
общепринятым обозначениям, запишем: |
|
∞ + ∞ = ∞; ∞ ∞ = ∞; |
1 |
= ∞; |
1 |
|
= 0; 0 0 = 0. |
|
0 |
∞ |
|||||
|
|
|
||||
Но если здесь все ясно, то отношение бесконечно больших функций, разность бесконечно больших функций, отношение бесконечно малых
5
функций, а также произведение бесконечно малой функции на бесконечно большую функцию есть неопределенности. Названные
неопределенности обозначаем |
∞ |
, ∞ − ∞, |
0 |
, 0 ∞ соответственно. |
|
∞ |
0 |
||||
|
|
|
Надо заметить, что каждая из перечисленных неопределенностей
имеет свои правила раскрытия. |
|
|
Правило раскрытия неопределенности |
∞ |
|
|
∞ |
|
Рассмотрим это правило на вычислении lim |
Pn (x) |
, где функцией |
|
||
x→∞ Qm (x) |
|
|
является отношение двух многочленов, т.е. рациональная функция. Исследуем отношение двух многочленов при условии, что аргумент x
становится и остается как угодно большим, т.е. x → ∞ . Заметим, что степень многочлена определяется старшей степенью переменной x . Приняты обозначения для многочленов степеней n и m соответственно:
Pn (x)= a0 + a1x + a2x2 + ...+ an−1xn−1 + anxn, Qm (x) = b0 + b1x + b2x2 + ...+ bm−1xm−1 + bmxm.
|
Ориентируясь только на старшие степени n или m многочленов Pn (x) |
|||||||||||||
и Q (x), можно утверждать, что lim |
P (x)= ∞, |
lim Q |
(x)= ∞ . |
|
|
|||||||||
|
m |
|
|
|
x→∞ |
n |
|
x→∞ m |
|
|
|
|
||
|
Пример 1. Найти |
lim |
5x3 − 4x2 + x −1 |
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x→∞ 7x2 + 8x +11 |
|
|
|
|
|
|
||||
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим |
многочлен третьей |
степени, |
находящийся |
в |
числителе, |
||||||||
5x3 − 4x2 −1= P |
(x), |
а |
многочлен |
второй |
степени, который |
записан |
в |
|||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
знаменателе, |
|
7x2 + 8x +11= Q |
(x). |
Анализируя |
|
многочлены |
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
P |
(x)= 5x3 − 4x2 |
−1 |
и |
Q (x)= 7x2 |
+ 8x +11, |
|
стоящие |
в |
числителе |
и |
||||
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
знаменателе соответственно, делаем вывод, что перед нами есть отношение двух бесконечно больших функций при условии, что аргумент x стремится к бесконечности. Это факт записывается
|
5x3 |
− 4x2 + x −1 |
|
∞ |
|
||
lim |
|
|
|
|
= |
. |
|
|
|
|
|
|
|||
x→∞ 7x2 + 8x +11 |
|
∞ |
|
||||
Анализируя степени 3 и 2 многочленов P3(x) |
и Q2 (x) соответственно, |
||||||
замечаем, |
что |
наибольшей степенью переменной x является 3. Эту |
|||||
степень дает |
многочлен |
P3(x), который в данном случае находится в |
|||||
числителе. |
Следует |
обратить внимание на |
определение степени 3 |
||||
6
переменной x как max{2,3} = 3. Выполним операцию почленного деления многочленов, стоящих в числителе и знаменателе, на x3. Будем иметь
|
|
|
5x3 − 4x2 |
|
+ x −1 |
|
|
|
|
|
∞ |
|
|
|
|
|
(5x3 − 4x2 + x −1) |
/ x3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= |
|
lim |
|
(7x2 + 8x +11)/ x3 |
= |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
x→∞ 7x2 + 8x +11 |
|
|
|
|
|
∞ |
x→∞ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
5x3 |
|
− |
4x2 |
+ |
|
x |
|
|
− |
1 |
|
|
|
|
5 |
− lim |
4 |
+ lim |
1 |
− lim |
1 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
x3 |
|
|
|
|
|
x3 |
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
= lim |
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
= |
1 |
|
x→∞ x x→∞ x2 |
|
x→∞ x3 |
|
= |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x→∞ |
|
7x2 |
|
|
8x |
11 |
|
|
|
|
|
|
|
|
|
|
lim |
7 |
+ lim |
8 |
+ lim |
11 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
3 |
|
+ |
x |
3 |
+ |
|
x |
3 |
|
|
|
|
|
|
|
|
|
x→∞ x x→∞ x2 |
x→∞ x3 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
5 |
= ∞. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
lim |
4 |
|
= lim |
|
|
1 |
|
|
= lim |
1 |
|
= lim |
7 |
= lim |
8 |
= lim |
11 |
= 0. |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x→∞ x x→∞ x2 |
|
|
x→∞ x3 |
|
x→∞ x x→∞ x2 |
|
x→∞ x3 |
|
||||||||||||||||||||||||||||||||||||||||||||
Ответ: |
lim |
|
5x3 − 4x2 |
|
+ x −1 |
= ∞. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
7x2 + 8x +11 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Пример 2. Найти |
|
|
lim |
|
−8x2 + 4x − 3 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ 6x5 − 3x2 + x − 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Решение
Видим, что перед нами есть вновь отношение двух бесконечно больших функций при условии, что аргумент x стремится к бесконечности.
Многочлен |
второй |
степени |
−8x2 + 4x −1= P |
(x) |
находится |
в числителе, |
|
|
|
2 |
|
|
|
многочлен |
пятой |
степени |
6x5 − 3x2 + x − 2 = Q |
(x) − в |
знаменателе. |
|
|
|
|
|
5 |
|
|
Анализируя степени многочленов P2 (x) и Q5 (x), замечаем, что наибольшей степенью переменной x является 5. Эту степень дает многочлен Q5 (x), и находится многочлен с более высокой степенью в знаменателе. Наивысшую степень 5 переменной x определили как max{2,5} = 5. Выполним операцию почленного деления многочленов P2 (x)
и Q5 (x), стоящих в числителе и знаменателе соответственно, на x5 . Получим
7
|
−8x2 |
+ 4x − 3 |
|
∞ |
|
|
(−8x2 + 4x − 3)/ x5 |
|
||
lim |
|
|
= |
|
= |
lim |
|
|
|
= |
|
|
|
|
+ x − 2)/ x5 |
||||||
x→∞ 6x5 − 3x2 + x − 2 |
|
∞ |
|
x→∞ (6x5 − 3x |
2 |
|
||||
|
|
|
|
|
|
− |
8x2 |
|
|
+ |
|
4x |
|
− |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
8 |
+ |
|
4 |
|
− |
3 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
x5 |
x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
x5 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
|
|
= lim |
|
|
|
|
|
|
x3 |
|
|
|
|
= |
|
|
|
||||||||||||||||||||||||||||||||||
5 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
x→∞ |
6x |
|
|
− |
|
|
3x |
+ |
|
|
x |
|
− |
2 |
|
|
|
x→∞ |
|
|
− |
|
|
+ |
|
|
− |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
x3 |
x4 |
x5 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|
|
|
5 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
− lim |
|
8 |
|
+ lim |
|
4 |
|
|
− lim |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= |
|
|
x→∞ x3 |
|
|
x→∞ x4 |
|
|
x→∞ x5 |
|
|
|
= |
|
0 |
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
− lim |
3 |
|
|
+ |
lim |
1 |
|
− |
lim |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
|
x→∞ x3 |
|
|
|
|
x→∞ x4 |
|
|
|
x→∞ x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Здесь lim |
|
8 |
|
|
= lim |
|
4 |
|
|
= lim |
|
|
3 |
|
|
|
= lim |
3 |
|
= lim |
1 |
= lim |
2 |
= 0. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x→∞ x3 |
|
|
x→∞ x4 |
|
|
x→∞ x5 |
|
|
|
|
|
x→∞ x3 |
|
|
x→∞ x4 |
x→∞ x5 |
|
|||||||||||||||||||||||||||||||||||||||||||
Ответ: |
lim |
|
−8x2 + 4x − 3 |
|
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
x→∞ 6x5 − 3x2 + x − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Пример 3. Найти |
|
lim −6x3 + 8x2 −12x + 3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
7x3 − 4x + 9 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Решение
И в этом случае имеем отношение двух бесконечно больших функций при условии, что аргумент x стремится к бесконечности. В числителе и в
знаменателе |
|
|
|
|
|
|
находятся |
|
|
|
|
многочлены |
|
|
|
|
|
|
|
третьей |
степени: |
|||||||||||||||||||||||||||||
−6x3 + 8x2 −12x + 3 = P |
(x) |
и 7x3 − 4x + 9 = Q |
(x). Степени этих многочленов |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
одинаковы, |
|
в |
данном |
|
случае |
это 3. |
Выполним |
|
|
почленное |
деление |
|||||||||||||||||||||||||||||||||||||||
многочленов |
|
|
|
P |
(x) |
|
|
и |
|
|
|
Q (x) на |
x3. |
|
В |
|
результате |
элементарных |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
преобразований будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
12x |
|
|
3 |
|
|
|
|
||||
|
|
|
−6x3 + 8x2 −12x + |
|
|
|
|
|
|
|
|
|
|
|
− |
6x |
+ |
8x |
− |
|
+ |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
3 |
|
∞ |
|
3 |
3 |
3 |
3 |
|
|
||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
= lim |
|
|
x |
|
|
|
x |
|
|
|
|
|
x |
|
|
|
x |
|
= |
|
|||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x→∞ |
|
|
|
7x |
− 4x + 9 |
|
|
|
|
|
∞ |
|
|
|
x→∞ |
|
7x |
− |
|
4x |
|
+ |
9 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
x3 |
|
|
|
x3 |
|
|
||||||||||
|
− |
6 |
+ lim |
8 |
− lim |
12 |
|
+ lim |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
1 |
|
x→∞ x x→∞ x2 |
|
|
|
x→∞ x3 |
= − |
6 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
7 |
|
− |
|
lim |
4 |
+ |
|
lim |
9 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
x→∞ x2 |
|
|
x→∞ x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Здесь
8
lim |
8 |
= lim |
12 |
= lim |
3 |
= lim |
|
4 |
= lim |
9 |
= 0. |
|||
|
|
|
|
|
|
|||||||||
x→∞ x |
x→∞ x2 |
x→∞ x3 |
x→∞ x2 |
|
x→∞ x3 |
|
||||||||
Ответ: lim |
−6x3 + 8x2 −12x + 3 |
= − |
6 |
. |
|
|
||||||||
|
7x3 − 4x + 9 |
7 |
|
|
||||||||||
|
|
x→∞ |
|
|
|
|
|
|
||||||
Анализ решений приведенных примеров позволяет сделать вывод. Пусть в роли бесконечно больших функций выступают многочлены, их называют еще полиномами, а это возможно при стремлении аргумента x к
∞
бесконечности. Отношение таких функций есть неопределенность ∞ .
Если многочлен с наибольшей степенью находится в числителе, то в ответе получаем бесконечно большое число, которое как абстракцию обозначаем ∞.
Если же многочлен с наибольшей степенью находится в знаменателе, то в ответе имеем 0, как предел бесконечно малой величины (ранее отметили, что бесконечно малая величина есть величина, обратная бесконечно большой).
Если степени многочленов оказываются равными, то в пределе имеем отношение коэффициентов, стоящих при старших степенях многочленов. Заметим, что именно старшая степень переменной многочлена и определяет его степень.
Сформулированный выше вывод можно очень кратко представить
вматематической символике:
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∞, |
если n > m, |
|
||
|
P |
(x) |
|
∞ |
|
|
|
||
|
|
|
|
||||||
lim |
n |
|
= |
|
= 0, |
если n < m, |
|
||
|
(x) |
|
|||||||
x→∞ Q |
|
∞ |
a |
|
|
||||
|
m |
|
|
|
|
||||
|
|
|
|
|
|
n |
, если n = m. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
b |
|
|
||
|
|
|
|
|
m |
|
|
||
Правило раскрытия неопределенности вида |
0 |
||||||||
0 |
|||||||||
|
|
|
|
|
|
|
|
||
Сначала рассмотрим отношение многочленов, которые при условии, что переменная x стремится к некоторому наперед заданному числу a , обращаются в бесконечно малые величины,
|
P (x) |
|
0 |
|
|
т. е. lim |
n |
= |
|
. |
|
|
|
|
|||
x→a Qm (x) |
|
0 |
|
||
Тот факт, что |
многочлены Pn (x) и Qm (x) |
при подстановке x = a |
|||
обращаются в нули, говорит о том, что число |
a является корнем этих |
||||
9

многочленов. А это означает, что и многочлен |
Pn (x) степени n , и |
|||||||
многочлен |
Q (x)степени |
m |
делятся |
на |
(x − a) |
без остатка1, т. е. |
||
|
m |
|
|
|
|
|
|
|
Pn (x) = (x − a)Rn−1(x) и Qm (x) = (x − a)Sm−1(x). Здесь |
Rn−1(x) |
− частное от |
||||||
деления многочлена Pn (x) |
на |
линейный |
двучлен |
(x − a). |
Это |
вновь |
||
многочлен, |
но степень его |
уже |
на единицу |
меньше, т. е. |
равна |
n −1. |
||
Совершенно аналогично можно сказать, что многочлен Sm−1(x)степени m −1 есть частное от деления многочлена Qm (x) на линейный двучлен
(x − a). Если теперь посмотреть на поставленную задачу о нахождении предела и выполнить предложенные преобразования
|
Pn (x) |
|
0 |
|
|
(x − a)Rn−1 |
(x) |
, то заметим, что двучлен (x − a) |
|
lim |
|
= |
|
|
= |
lim |
|
|
|
|
|
|
(x) |
||||||
x→a Qm (x) |
|
0 |
|
x→a (x − a)Sm−1 |
|
||||
можно сократить. Следует обратить внимание на то, что не нули сокращаем, а одинаковые бесконечно малые величины, поскольку x ≠ a, но x → a , и разность (x − a) является бесконечно малой величиной.
Отсюда следует вывод: если отношение многочленов при x → a
обращается |
в отношение |
бесконечно малых величин, то уже известен |
|||
множитель, |
который дает |
ноль. Это (x − a) |
или |
(a − x). |
Разложите |
многочлены на простейшие множители. Сократив |
бесконечно малые |
||||
величины (x − a) или (a − x), можно получить |
результат. |
Этот метод |
|||
0
позволит избавиться от неопределенности , или, как говорят, раскрыть
0
ее.
|
|
Пример 4. Найти lim |
x2 − 5x + 6 |
. |
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
x→2 |
x2 − 2x |
|
|
||||
|
|
Решение |
|
|
|
|
|
|
||
|
|
При подстановке предельного значения аргумента x = 2 в выражение |
||||||||
|
x |
2 − 5x + 6 |
имеем отношение |
|
0 |
, а это отношение не определено. В этом |
||||
|
|
x2 − 2x |
0 |
|||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0 |
|
случае говорят, что имеем неопределенность вида |
|
. |
||||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Поскольку многочлены |
второй степени (квадратные трехчлены) |
|||||||
1 Здесь рассматривается следствие теоремы Безу о делении многочлена f(x) на линейный двучлен (x-a): число а является корнем многочлена f(x) тогда и только тогда, когда f(x) делится без остатка на двучлен (x-a). Этьен Безу (Etienne Bezout, 1730 − 1783) − французский математик. Основные труды посвящены алгебре.
10

x2 − 5x + 6 и x2 − 2x обращаются в ноль при подстановке x = 2, то это означает, что каждое из уравнений x2 − 5x + 6 = 0 и x2 − 2x = 0 имеет своим
корнем x = 2. Следовательно, в выражениях x2 − 5x + 6 и x2 − 2x можно выделить разность (x − 2) как бесконечно малую величину при x → 2.
Решим уравнение x2 − 5x + 6 = 0. Найдем его корни: x = 2 и x = 3 (это видно из теоремы Виета2: 2+3=5, 2 3=6). Разложим квадратный трехчлен x2 − 5x + 6 на множители: x2 − 5x + 6 = (x − 2)(x − 3).
Преобразование же выражения x2 − 2x : x2 − 2x = x(x − 2) очевидно. Видим, что и в числителе, и в знаменателе удалось выделить
одинаковый множитель – бесконечно малую функцию (x − 2) |
при x → 2. |
Сократим одинаковые бесконечно малые величины (x − 2). |
Результат |
получим при подстановке в оставшееся выражение предельного значения
аргумента |
x , т.е. x = 2. Решение будет таким: |
|
|
|
|
|
|
||||||||||||
lim |
x2 − 5x + 6 |
= lim |
(x − 2)(x − 3) |
lim |
x − 3 |
= − |
1 |
. |
|
|
|
|
|||||||
|
|
|
|
|
x(x − 2) |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x→2 x2 − 2x |
|
|
x→2 |
|
x→2 x |
|
2 |
|
|
|
|
|
|||||||
Ответ: |
lim |
x |
2 − 5x + 6 |
= − |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
x2 − 2x |
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x→2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вывод. |
|
|
Чтобы |
раскрыть |
неопределенность вида |
|
0 |
, надо |
|||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
выделить в числителе и знаменателе одинаковые множители, это будут при x → a бесконечно малые величины − либо (x − a), либо (a − x), и сократить эти бесконечно малые величины.
Правило раскрытия неопределенности вида ∞ − ∞
Пример 5. Найти lim 
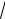 x − 2 −
x − 2 − 
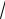 x + 4 .
x + 4 .
x→∞
Решение
Имеем разность двух бесконечно больших функций при условии, что аргумент x стремится к бесконечности. Этот факт записываем как
lim 
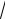 x − 2 −
x − 2 − 
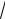 x + 4 = (∞ − ∞). x→∞
x + 4 = (∞ − ∞). x→∞
2 Виет (Вьет) Франсуа (Viete Francois) (1540 – 1603) – французский математик, по профессии – юрист. Интересовался астрономией и пришел через нее к тригонометрии и алгебре. Получил решение уравнений 2-й, 3-й и 4-й степени в радикалах. Ввел впервые буквенные обозначения не только неизвестных величин, но и для данных – коэффициентов уравнений.
11

Выражение 
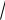 x − 2 +
x − 2 + 
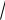 x + 4 называется сопряженным по отношению к
x + 4 называется сопряженным по отношению к
|
|
|
|
|
|
|
|
|
|
исходному |
x − 2 − |
x + 4 . Заметим, что |
в сопряженном выражении |
||||||
|
|
|
|
|
|
|
|
||
|
x − 2 + x + 4 |
нет |
неопределенности, |
действительно, сумма двух |
|||||
бесконечно больших величин есть бесконечно большая величина, т. е.
lim (
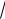 x − 2 +
x − 2 + 
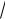 x + 4)= ∞ + ∞ = ∞ . Интересен тот факт, что произведение
x + 4)= ∞ + ∞ = ∞ . Интересен тот факт, что произведение
x→∞
двух взаимно сопряженных выражений позволяет избавиться от квадратных корней. Действительно, здесь используется одна из формул
сокращенного умножения: (a − b) (a + b) = a2 − b2. В нашем случае будем иметь
(
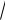 x − 2 −
x − 2 − 
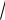 x + 4)(
x + 4)(
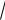 x − 2 +
x − 2 + 
 x + 4)= (x − 2)− (x + 4) = x − 2 − x − 4 = −6 .
x + 4)= (x − 2)− (x + 4) = x − 2 − x − 4 = −6 .
Выполним эквивалентные преобразования, суть дела не меняется, но внешний вид будет другим: умножим и числитель, и знаменатель на
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выражение |
x − 2 + |
x + 4 , |
сопряженное |
исходному |
|
x − 2 − x + 4 , и |
|||||||||||||||||||||||||
используем уже готовый промежуточный результат: |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
− |
|
)( |
|
|
+ |
|
) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 2 |
x + 4 |
x − 2 |
x + 4 |
|
|
|
|
|
||||||||
lim x − 2 − x + 4 = lim |
= |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x→∞ |
|
|
|
|
|
|
x→∞ |
|
|
( x − 2 + x + 4) |
|
|
|
|
|
||||||||||||||||
= lim |
|
|
|
−6 |
|
|
= |
−6 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x→∞ ( x − 2 + x + 4) |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Как видим, такое элементарное эквивалентное преобразование
исходного выражения позволило избавиться от неопределенности вида
(∞ − ∞).
|
|
|
|
|
|
|
|
Ответ: lim x − 2 − x + 4 = 0. |
|
||||||
x→∞ |
|
|
|
||||
|
|
|
|
x3 |
|
||
Пример 6. Найти lim |
|
|
|
− x . |
|||
|
2 |
|
|||||
|
|
|
|
− 5 |
|
||
|
|
x→∞ x |
|
|
|||
Решение
x3
Исследуем дробь x2 + 5 . Поскольку имеем отношение двух бесконечно больших функций при стремлении переменной x к бесконечности, то в
|
x3 |
|
∞ |
|
соответствии с выводами, полученными выше, имеем lim |
|
= |
|
= ∞. |
|
||||
x→∞ x2 − 5 |
|
∞ |
|
|
Таким образом, имеем разность двух бесконечно больших функций,
12
