ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник

Федеральное агентство связи

Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования

«Сибирский государственный университет телекоммуникаций и информатики»

(ФГОБУ ВПО «СибГУТИ»)

В.К. Трофимов, В.И. Агульник

ДИФФЕРЕНЦИАЛЬНОЕ

ИСЧИСЛЕНИЕ

Учебное пособие

Рекомендовано Сибирским региональным учебно-методическим центром высшего профессионального образования для межвузовского использования в качестве учебного пособия для студентов технических направлений и специальностей

Новосибирск

2013

УДК 517.3 (075.8)

Трофимов В.К, Агульник В.И.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ: Учебное пособие/ФГОБУ ВПО

«СибГУТИ». – Новосибирск, 2013 г. - 151 с.

Учебное пособие содержит теоретический материал и задачи по курсу математики, математического анализа для студентов 1 курса всех направлений и профилей технического вуза. Материал разбит на главы, в каждой из которых представлена теория по изучаемой теме, даны примеры решения задач и задачи для самостоятельного решения. Задания подобраны в соответствии с разработками кафедры высшей математики СибГУТИ. Большинство задач взяты из известных задачников Г.Н.Бермана, А.В.Ефимова, Б.П. Демидовича.

Учебное пособие может быть использовано для самостоятельного изучения студентами заочного отделения всех направлений технического вуза.

Кафедра высшей математики Стр. 150, илл. – 60, список литературы – 25 назв.

Для направлений 210700 Инфокоммуникационные технологии и системы связи, 230100 Информатика и вычислительная техника.

Рецензенты: д.ф.-м.н., проф. Черных Г.Г., к.т.н., доц. Григорьев Е.М.

Утверждено редакционно-издательским советом ФГОБУ ВПО «СибГУТИ» в качестве учебного пособия.

©Сибирский государственный университет телекоммуникаций и информатики, 2013 г.

2

ОГЛАВЛЕНИЕ ПРЕДИСЛОВИЕ ……………………………………………………………….........5

Раздел I. ВВЕДЕНИЕ В АНАЛИЗ …………………………………………………6

Глава 1. Понятие числа ………………………………………………………….6

§1.1. Множество действительных чисел ……………………………….......6 §1.2. Числовая ось. Модуль действительного числа ...…………………….7

§1.3. Определение комплексного числа. Алгебраическая форма записи комплексного числа …………………………………………………...9

§1.4. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числа ………………………………………11

§1.5. Умножение комплексных чисел в тригонометрической форме.

Формула Муавра ……………………………………………………..14 §1.6. Извлечение корня степени п ………………………………………….15

Глава 2. Функция …………………………………………….………………...18 §2.1. Понятие функции. Способы задания функции ……………………..18 §2.2. Простейшие свойства функций ……………………………………...21 §2.3. Понятие обратной функции ………………………………………….24

§2.4. Элементарные функции ……………………………………………...26 §2.5. Задание функции в полярных координатах ………………………...31 §2.6. Уравнение кривой в параметрическом виде ………………………..34

Глава 3. Теория пределов ……………………………………………………...36 §3.1. Предел функции ………………………………………………………36

§3.2. Бесконечно малая величина и её свойства ………………………….39

§3.3. Свойства пределов ……………………………………………………41

§3.4. Свойства пределов, связанные с неравенствами …………………..43 §3.5. Первый замечательный предел ……………………………………...44 §3.6. Второй замечательный предел ………………………………………45

§3.7. Сравнение бесконечно малых величин …………………………….48

§3.8. Эквивалентные бесконечно малые величины и их свойства ……...49 §3.9. Вычисление пределов с помощью эквивалентных величин …….....51 §3.10. Односторонние пределы …………………………………………….52

Глава 4. Непрерывные функции и их свойства ………………………………55

§4.1. Непрерывность функции в точке ……………………………………55

§4.2. Точки разрыва и их классификация ………………………………...56 §4.3. Свойства функций, непрерывных в точке и на интервале ………..58

Раздел II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ …………………………...62 Глава 1. Производная и дифференциал ……………………………………….62

§1.1. Определение производной …………………………………………..62 §1.2. Геометрический смысл производной. Уравнение касательной …...64 §1.3. Правила дифференцирования ……………………………………….65

§1.4. Производные элементарных функций ……………………………...67 §1.5. Дифференциал ………………………………………………………..75 §1.6. Производные и дифференциалы высших порядков ………………78

Глава 2. Основные теоремы дифференциального исчисления ……………...80

3

§2.1. Теорема Ролля ………………………………………………………..80 §2.2. Теорема Лагранжа о конечных приращениях………………………81

§2.3. Теорема Коши ………………………………………………………..82 §2.4. Формула Тейлора …………………………………………………….83

§2.5. Правило Лопиталя ……........................................................................89 §2.6. Виды неопределенностей и их раскрытие …….................................91

Глава 3. Исследование функций ………………………………………………96

§3.1. Условия возрастания и убывания функций ………………………...96 §3.2. Экстремум функции. Необходимое условие ………………………97

§3.3. Достаточные условия экстремума …………………………………. 99 §3.4. Выпуклость и вогнутость графика функции ……………………...102 §3.5. Асимптоты графика функции и их нахождение ………………….105

§3.6. Построение графика функции ……………………………………..107

Раздел III. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ ……………………..111 Глава 1. Основные понятия и свойства функции нескольких

переменных …………………………………………………………...111 §1.1. Понятие функции нескольких переменных ……………………….111

§1.2. Предел функции двух переменных ………..……………………....113 §1.3. Непрерывность функции двух переменных ………………………115

Глава 2. Дифференциальное исчисление функций двух переменных …….118 §2.1. Частные производные ……………………………………………...118 §2.2. Дифференциал ………………………………………………………120

§2.3. Дифференцирование сложной функции и неявной функции ……122 §2.4. Частные производные и дифференциалы высших порядков ……126 §2.5. Формула Тейлора для функции двух переменных ……………….128

Глава 3. Исследование функций двух переменных ………………………...130 §3.1. Скалярное поле и его геометрия …………………………………...130 §3.2. Производная по направлению ……………………………………...131 §3.3. Градиент ……………………………………………………………..132 §3.4. Касательная плоскость и нормаль к поверхности ………………...134 §3.2. Экстремум функции двух переменных ……………………………136

Ответы к задачам …………………………………………………………………141

Список литературы ……………………………………………………………….149

4

ПРЕДИСЛОВИЕ Предмет, основы которого излагаются в этом пособии, носит название

«математический анализ», – название, которое студенты сокращают: «матанализ», или даже: «матан». Полное название этой дисциплины, однако, не только более длинное: «математический анализ функций с помощью дифференциального и интегрального исчислений», но и даёт представление о том, чем занимается данная часть высшей математики. Основная идея дифференциального исчисления заключается в изучении и исследовании локальных свойств функции для описания свойств функции в целом.

Основателями дифференциального исчисления по праву считаются английский ученый И.Ньютон и немецкий ученый Г.Лейбниц. В их трудах были введены основные понятия дифференциального исчисления – производная и дифференциал. И.Ньютон разработал теорию флюксий (в современной терминологии – производных). В работах Г.Лейбница, независимо от И. Ньютона, дифференциальное исчисление построено на основе понятия дифференциала. Оба этих понятия, как и важнейшее – непрерывность, базируются на идее предела.

Впрочем, отдельные задачи дифференциального исчисления, связанные с нахождением максимума и минимума некоторых функций, а также с вычислением касательных к некоторым кривым, были решены еще математиками Древней Греции.

Вначале XIX века в трудах Ш. Лагранжа, О. Коши, Б. Тейлора, К. Гаусса, Л. Эйлера дифференциальное исчисление обрело достаточно законченную форму, а курс этого раздела математического анализа принял классический вид.

Внастоящем пособии вводимые идеи и понятия по возможности подробно поясняются большим количеством примеров и иллюстраций. Каждый из трёх разделов снабжен набором задач для самостоятельного решения, а задачи – ответами, помещенными в конце пособия.

Пособие рассчитано на студентов 1 курса всех технических направлений и профилей как дневного, так и заочного обучения. Электронный вариант пособия доступен также студентам, обучающимся с применением дистанционных технологий.

5

РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ

Глава 1. Понятие числа

§1.1. Множество действительных чисел

В этом разделе мы дадим общие сведения о действительных числах, необходимые для усвоения материала, изложенного в книге. Понятие действительного числа будет дано на основании интуитивного представления и знаний, полученных в средней школе.

Читателю, заинтересованному в более полном изучении этого вопроса, можно рекомендовать учебники [1-19].

Хорошо известно, что целые положительные числа образуют множество, называемое множеством натуральных чисел и обозначаемое в дальнейшем буквой N:

N = {1, 2, 3,…} .

Добавляя к натуральным числам число 0 и целые отрицательные числа, получим множество всех целых чисел, которое обозначают Z:

Z = {…, −3, −2, −1, 0,1, 2,3,…} .

Числа, представимые в виде несократимой дроби qp , где p и q – целые числа, а q > 0 , называются рациональными числами и обозначают Q. Так как любое целое число n представимо в виде n = 1n , то это означает, что все целые

числа – рациональные. Часто используется эквивалентное определение рационального числа: рациональными называются числа, которые можно представить в виде конечной десятичной или бесконечной периодической дроби.

Действительные числа, не являющиеся рациональными, называются иррациональными. Возникает вопрос: существуют ли иррациональные числа? Положительный ответ на этот вопрос даёт следующее утверждение:

Утверждение 1. Число 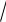2 является иррациональным числом.

Доказательство. Проведем доказательство методом от противного. По

Так как правая часть (1.1) делится на 2, то и левая делится на 2, но это в свою очередь означает, что р делится на 2, т.е. p2 делится на 4. Тогда из (1.1)

6

следует, что 2q2 делится на 4, т.е. q2 делится на 2, а значит, q делится на 2,

противоречие доказывает наше утверждение.

Примером иррационального числа служит десятичная дробь вида

0,101001000100001…

Здесь серия нулей после каждой единицы увеличивается на один нуль по сравнению с предшествующей серией нулей. Иррациональность этого числа следует из того факта, что выписанная десятичная дробь не обладает периодом.

§1.2. Числовая ось. Модуль действительного числа

Множество всех действительных чисел, включающее в себя рациональные и иррациональные числа, обозначим R .

На протяжении изучения основ математического анализа значительную роль играет геометрическое изображение чисел. Для такого представления действительных чисел возьмём прямую линию и на ней зафиксируем точку О, которая является началом отсчёта длин, выберем масштаб, т.е. отрезок, длина которого принимается за единицу, и установим направление отсчёта. Обычно, справа от О – положительные числа, слева – отрицательные.

По определению, прямую линию, на которой указаны начало отсчёта, масштаб и направление отсчёта, называют числовой осью (рис. 1.1).

существует взаимно-однозначное соответствие между числами и точками числовой оси, поэтому точку числовой оси, соответствующую числу α, будем обозначать также α. Точка О соответствует числу «ноль».

На числовой оси наглядно представляются различные соотношения между числами. Меньшему числу соответствует точка, лежащая левее точки, изображающей большее число. Числу, заключенному между двумя данными числами, соответствует точка, лежащая между точками, изображающими данные числа.

Приведём ещё несколько определений и следствий из них, которые будут использоваться нами на протяжении всего последующего изложения.

Определение 1.1. Абсолютной величиной (модулем) a числа a называется

число, определяемое следующим образом:

a, если a ≥ 0, a = −a, если a < 0.

7

Из определения следует, что a > 0 для всех чисел a таких, что a ≠ 0 ,

равносильно двойному неравенству

−ε < x < ε .

Соотношение (1.2) означает, что точка x отстоит от точки О на расстоянии не более чем ε , а это возможно только в том случае, когда x принадлежит интервалу (−ε, ε) .

Приведем некоторые свойства абсолютной величины, непосредственно вытекающие из определения:

1. Абсолютная величина суммы не превосходит суммы абсолютных величин слагаемых, т.е.

a1 + a2 + + an ≤ a1 + a2 + + an .

2. Абсолютная величина разности не меньше разности абсолютных величин a − b ≥ a − b .

8

−∞ < x < +∞ . Запись [a;b] (c; d ) означает, что все точки отрезка [a;b] принадлежат интервалу (c; d ).

Определение 1.5. Множество точек x, удовлетворяющих неравенству

§1.3. Определение комплексного числа. Алгебраическая форма записи комплексного числа

Решение уравнения вида x2 − 2 = 0 привело нас к понятию иррационального числа. Однако не все квадратные уравнения имеют решение, выражаемое рациональным или иррациональным числом, т.е. разрешимое в

действительных числах. Например, чтобы решить уравнение x2 + 2 = 0 , необходимо расширить множество действительных чисел. Это можно сделать, если ввести понятие комплéксного числа.

которого выяснится ниже). При этом a называется действительной частью числа z и обозначается a = Re z ; b называется мнимой частью числа z и обозначается b = Im z .

Два комплексных числа z1 = a1 + b1i и z2 = a2 + b2i равны тогда и только тогда, когда равны их действительные и мнимые части, т.е. a1 = a2 и b1 = b2

Арифметические операции над комплексными числами определяются следующим образом:

- суммой чисел a1 + b1i и a2 + b2i называется число

(a1 + a2 ) + (b1 + b2 )i ;

- разностью чисел a1 + b1i и a2 + b2i называется число

(a1 − a2 ) + (b1 − b2 )i ;

-произведением чисел a1 + b1i и a2 + b2i называется число

a1a2 – b1b2 + (a1b2 + a2b1)i.

Определенные таким образом операции удовлетворяют всем правилам сложения и умножения действительных чисел:

1)коммутативность сложения z1 + z2 = z2 + z1 ,

2)ассоциативность сложения (z1 + z2 ) + z3 = z1 + (z2 + z3 ) ,

3)коммутативность умножения z1 z2 = z2 z1 ,

4)ассоциативность умножения (z1 z2 ) z3 = z1 (z2 z3 ),

9

5)дистрибутивность умножения относительно сложения

(z1 + z2 ) z3 = z1 z3 + z2 z3 .

Таким образом, сложение, вычитание и умножение комплексных чисел

подмножеством множества комплексных чисел.

Числа 0 + bi называют чисто мнимыми и обозначают bi. Например, 0 – 2i = -2i, 0 + 1i = i. Смысл символа i вытекает из формулы (1.4):

умножения двучленов и затем, в соответствии с формулой (1.5), заменить i2 на –

1.

Рассмотрим примеры.

Пример 1.1. Найти сумму и произведение двух сопряженных комплексных чисел z = x + yi

и z = x − yi .

Решение. По формуле (1.3) находим сумму чисел

z + z =(x + x) +(y − y)i = 2x .

Произведение находим формальным перемножением

z z = (x + yi )(x − yi) = x2 − y2i2 = x2 + y2 .

И в том, и в другом случае получаем в результате действительные числа.

Формула (1.6) для деления комплексных чисел получается, если числитель и знаменатель дроби умножить на число, сопряженное знаменателю, и после этого раскрыть скобки. Например, для частного двух сопряженных чисел:

Пример 1.2. Даны комплексные числа z1 = −1+ 6i и z2 = 2 + 5i . Найти разность z2 – z1 и

частное z2/z1.

Решение. По формуле (1.3) находим

10