лекция 1 (10.02.05)

Введение

Дискретная математика представляет собой область математики, в которой изучаются свойства структур конечного характера, а также бесконечных структур, предполагающих скачкообразность происходящих в них процессов или отделимость составляющих их элементов. В отличие от дискретной математики классическая математика занимается изучением свойств структур непрерывного характера. Это деление достаточно условно, поскольку средства дискретной математики используются для изучения непрерывных моделей и наоборот.

Бурное развитие дискретной математики обусловлено прогрессом компьютерной техники, необходимостью создания средств обработки и передачи информации, а также представления различных моделей на компьютерах, которые по своей природе являются структурами конечными.

1. Элементы теории множеств

1. Множества и их спецификация

   1. Элементы и множества

Понятие множества относится к числу фундаментальных понятий математики.

Под множеством понимают совокупность определенных различаемых объектов, таких, что для любого объекта можно установить, принадлежит он данному множеству или нет.

1. Можно рассматривать множества объектов любой природы: множество городов России, множество студенческих групп на факультете ИВТ, множество букв русского языка, множество натуральных чисел…

Сами объекты, из которых состоит множество, называются его элементами. Все элементы множества различны и отличимы друг от друга.

• Множества обычно обозначают прописными буквами (А, В, С и т.д.), а их элементы – строчными (например: x, y, z).

Если элемент x принадлежит множеству А, то пишут x  A. Запись x  A означает, что элемент x не принадлежит множеству А.

Множества, как объекты, могут быть элементами других множеств. Множество, элементами которого являются другие множества, обычно называется семейством, или классом множеств.

• Обычно семейства множеств обозначают рукописными буквами латинского алфавита для отличия их от обычных множеств.

Множество, не содержащее элементов, называется пустым множеством и обозначается символом .

Если все рассматриваемые множества (в конкретной задаче) являются подмножествами более широкого множества U, то множество U называется универсальным множеством, или универсумом.

Мощность множества M обозначается как |M| и для конечного множества равняется числу элементов в нем.

• Заметим, что || = 0, но |{}| = 1.

Для числовых множеств здесь и далее будем использовать следующие обозначения: N – множество натуральных чисел, Z – множество целых чисел, R – множество действительных чисел, P – множество простых чисел, Q – множество рациональных чисел.

2. Задание множеств. Парадокс Рассела

2. Рассмотрим несколько множеств:

1. А = {2, 4, 6}; 2) B = {1, 3, 5}; 3) C = {A, B}; 4) D = {x R | x>0}; 5) E = {2·y | y=1, 2, …, n}; {мн-во четных чисел} 6) F = {x | x=1 или x=2·y, yF } {степени двойки: 1, 2, 2², 2³, 2⁴, …}

В первом и втором пунктах примера множества заданы путем перечисления их элементов. В третьем пункте – тоже, но здесь элементами множества C являются множества. Заметим, что множество C имеет только два элемента и, в частности, 1 C, хотя 1 A  и A C . Действительно: 1A и 1B,  1 C, т.к. только A и B являются элементами C.

В 4-м примере множество D задано путем его описания, т.е. задания неких свойств его элементов.

Множества E, F строятся согласно указанному способу порождения множества, т.е. с помощью задания некой процедуры построения, причем множество F определяется через его же элементы. Правило задания F является рекурсивным.

Задание множества путем указания его свойств может приводить к противоречиям. Например, один из наиболее типичных теоретико-множественных парадоксов носит название парадокса Рассела и состоит в следующем. Рассмотрим множество всех множеств, которые не содержат себя в качестве элемента: F = {X | XX}. Спрашивается, является ли само множество F элементом F? Возможны только два случая:

1) FF. Тогда для него выполняется условие содержания элемента в множестве, т.е. FF.

2) FF. Тогда для F не выполняется условие содержания элемента в множестве, т.е. F содержит само себя: FF.

Получается, что в обоих случаях пришли к противоречию. Рассмотрение «бесконечно больших» множеств, элементами которых в свою очередь являются множества, невозможно в рамках обычной теории множеств и требует математики другого рода.

Потому мы будем рассматривать только те множества, которые могут быть явно записаны или построены путем четко определенных процессов. Для каждого множества должна быть определена его спецификация. Итак, множества могут быть заданы тремя основными способами:

1. Перечислением элементов множества (множества A, B, C) {1,2,3}.

Этот способ применим только для конечных множеств.

2. Указанием свойств элементов множества, или заданием т.н. характеристического предиката: D = {x | P(x)} (Другими словами – задание разрешающей процедуры).

Здесь P(x) обозначает некоторое условие, выраженное в форме логического утверждения; это условие может быть проверено для любого элемента.

3. Порождающей процедурой: E = {y | y:=f(x)}.

Такая процедура описывает способ получения элементов множества из уже полученных элементов или из других объектов. Элементами множества считаются все объекты, которые могут быть получены с помощью такой процедуры.

2. Операции над множествами

   1. Сравнение множеств

Если каждый элемент множества А является элементом множества В, то пишут А  В (А является подмножеством множества В). Считается, что   А для любого множества А.

Подмножество C множества B называется его собственным подмножеством, если C  В, но C  В. Обычно для обозначения этого факта используется символ : C  В.

Два множества равны, если они состоят из одних и тех же элементов. Равенство множеств обозначается как А = В. Если множества не равны, то пишут А  В.

Множество А равно множеству В, если А  В и В  А.

Для числовых множеств выполняется N  Z  R.

3. Обратимся к примеру 1.2: А = {2, 4, 6}; B = {1, 3, 5}; C = {A, B}. Очевидно, что А  C, но тем не менее А  C, поскольку ни один из элементов А не является элементом C (т.е. множество А является элементом множества C, но А не является подмножеством множества C.

Если |А| = |В|, то такие множества называются равномощными.

2. Операции над множествами. Диаграммы Венна

Обычно рассматриваются следующие операции над множествами:

Объединением (или суммой) множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В: A  B = {x | x  A или x  B}.

Пересечением (или произведением) множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат каждому из множеств А и В: A  B = {x | x  A и x  B}.

Если A  B = , то множества А и В называются непересекающимися.

Разностью множеств А и В называется множество A \ B , состоящее из тех и только тех элементов, которые принадлежат А, но не принадлежат В: A \ B = {x | x  A и x  B}.

Симметрической разностью множеств А и В называется множество A Δ B = (A  B) \ (A  B) = {x | (x  A и x  B) или (x  B и x  A)}.

Дополнением множества А называется множество всех элементов универсального множества, не входящих в A: A = U \ A = {x |  x  A}.

Операции объединения и пересечения допускают обобщение для большего количества множеств (в том числе и бесконечного). В общем случае для объединения k множеств используется обозначение , или для бесконечного числа множеств: = {x |  i  I | x  A_i}. Аналогично, для пересечения k множеств используется обозначение , или , если количество множеств бесконечно: = {x |  i  I |x  A_i }.

Н а рисунке 1.1 (справа) приведены т.н. диаграммы Эйлера-Венна, графически иллюстрирующие вышеописанные операции над множествами. Введенные операции показаны на диаграммах Венна темным цветом. Такие геометрические представления множеств часто используются при решении задач или доказательстве каких-либо утверждений.

4. Рассмотрим два множества чисел: А = {1, 2, 3, 4}; B = {1, 3, 5, 7}. Тогда операции над этими множествами будут иметь вид: объединение A  B = {1, 2, 3, 4, 5, 7}; пересечение A  B = {1, 3}; разность A \ B = {2, 4} и B \ A = {5, 7}; симметрическая разность A Δ B = {2, 4, 5, 7}. Для рассмотрения дополнения A необходимо знать универсальное множество, все элементы которого за исключением элементов A и будут являться дополнением.

3. Представление множеств в ЭВМ

Задать представление какого-либо объекта в программе – означает описать в терминах используемой системы программирования структуру данных, используемую для хранения информации о представляемом объекте, и алгоритмы над выбранными структурами данных, которые реализуют присущие данному объекту операции.

Один и тот же объект может быть представлен различными способами, причем в разных ситуациях могут оказаться наиболее эффективными разные способы. Выбор представления зависит от целого ряда факторов: особенности представляемого объекта, состав и относительная частота использования операций в конкретной задаче, и т.д. Хороший программист должен знать разные способы представления объекта и в каждой конкретной ситуации уметь выбрать из них наиболее подходящий.

Для конечного универсума, мощность которого не превосходит разрядности машинного слова, подмножества универсума могут представляться битовой шкалой (аналог характеристической функции – 0 или 1 для каждого элемента). Тогда операции над подмножествами осуществляются посредством поразрядных логических операций.

Во многих переборных алгоритмах требуется последовательно рассмотреть все подмножества заданного множества. В случае использования битовой шкалы существуют специальные алгоритмы, которые будут рассмотрены позже.

Если универсум велик, а подмножества имеют сравнительно небольшую мощность, то использование характеристических функций невыгодно, т.к. в них будет много нулей. Для представления таких множеств обычно используют списки элементов. Элемент множества тогда может быть представлен записью с двумя полями: информационным и указателем на следующий элемент. Трудоемкость операций включения, пересечения и объединения определяется как O(mn), где m и n – мощности множеств; операции  – как O(n).

При использовании списков, упорядоченных по информационному полю, трудоемкость всех операций является линейной (О(n)). В таком случае эффективная организация всех операций над множествами основана на общем алгоритме, известном как алгоритм типа слияния.

Алгоритм типа слияния параллельно просматривает два множества, представленных упорядоченными списками, причем на каждом шаге продвижение происходит в том множестве, в котором текущий элемент меньше. В качестве простейшей организации множеств можно использовать упорядоченный массив элементов.

1. Проверка включения AB

Вход: Два упорядоченных множества A и B (массивы).

Выход: да или нет (1 или 0, true или false).

i:=1; j:=1; // указатели на начало множеств

пока i|A|+1 и j|B|+1 цикл

если A[i] < B[j] то вернуть 0 и выход // элемент A отсутствует в B

иначе если A[i] > B[j] то j:=j+1 // переход к след. элементу B

иначе // элементы совпали – перейти к следующим

i:=i+1; j:=j+1;

конец если

конец цикла

если i=|A|+1 то вернуть 1 иначе вернуть 0.

Алгоритмы, вычисляющие объединение множеств, пересечение и дополнение устроены совершенно аналогичным образом. Общее действие – продвижение вперед (увеличение индекса) в том массиве, элемент которого меньше, и сразу в обоих, если элементы равны.

Для определения объединения в результирующее множество заносятся каждый из меньших элементов и один, если они равны. Если конец одного из множеств достигнут раньше, все оставшиеся элементы другого дописываются в конец итогового множества.

Для определения пересечения в результирующее множество заносится тот элемент, который совпал у обоих множеств. Если конец одного из множеств достигнут раньше, работа алгоритма заканчивается.

лекция 2 (17.02.05)

4. Разбиения и покрытия

Пусть Ě ={E_i} для i I – некоторое семейство непустых подмножеств множества M, E_i  M. Тогда семейство Ě называется покрытием множества M, если каждый элемент множества M принадлежит хотя бы одному из E_i: M    x M  i I |  x E_i. (проилл-ть на диаграмме Венна)

Семейство Ě называется дизъюнктным, если элементы этого семейства попарно не пересекаются, т.е. каждый элемент множества M принадлежит не более чем одному из множеств E_i: i,j I, ij  E_i   E_j=. (илл. на д. Венна)

Дизъюнктное покрытие Ě называется разбиением множества M.

5. Пусть имеется множество M={1,2,3}. Тогда семейство {{1,2}, {2,3}, {3,1}} является покрытием, но не разбиением; семейство {{1},{2},{3}} – покрытием и разбиением, а семейство {{1},{2}} является дизъюнктным, но в то же время не является ни покрытием, ни разбиением.

Совокупность всех подмножеств множества M называется булеаном и обозначается P (M), или 2^M: 2^M = {A | A  M}.

6. Пусть имеется множество M = {1,2,3}. Тогда булеаном для него будет являться семейство {,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}

5. Свойства операций над множествами

Пусть задан универсум U. Тогда A, B, C  U выполняются свойства:

1. Идемпотентность

   A  A = A

   A  A = A

2. Коммутативность

   A  B = B  A

   A  B = B  A

3. Ассоциативность

   A  (B  C) = (A  B)  C

   A  (B  C) = (A  B)  C

4. Дистрибутивность

   A  (B  C) = (A  B)  (A  C)

   A  (B  C) = (A  B)  (A  C)

5. Операции с пустым множеством (свойства нуля)

   A   = A

   A   = 

6. Операции с универсальным множеством (свойства единицы)

   A  U = U

   A  U = A

7. Свойства дополнения

   Инволютивность:

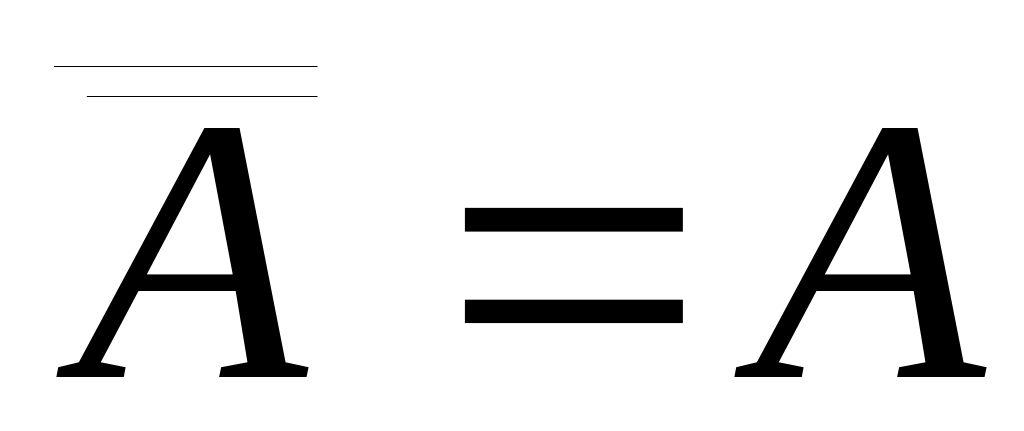
   A A = U A A=

8. Поглощение

   (A  B)  A = A

   (A  B)  A = A

9. Двойственность (законы де Моргана)

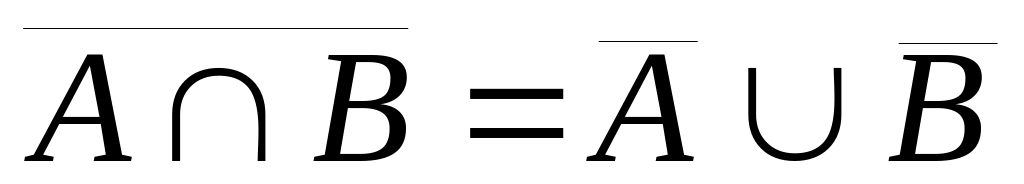
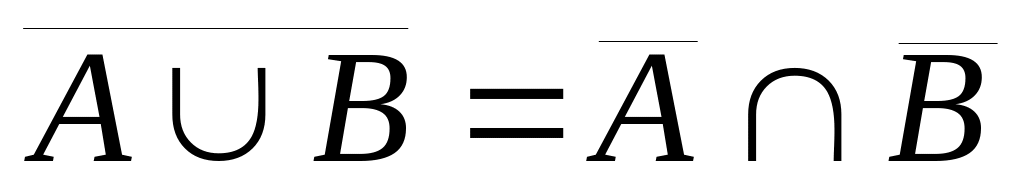
10. Выражение для разности

A \ B = A B

В справедливости перечисленных свойств легко убедиться, причем это можно сделать различными способами. Например, проверить каждое равенство по определению или же воспользоваться геометрическим представлением с помощью диаграмм Венна.

На основании свойств 1–10 можно получить новые свойства и равенства.

П ример для общего развития: Разные способы определения симметрической разности. Можно не приводить на лекции; лучше рассмотреть на практике. Доказать, что верно равенство (AB)\(AB)(A\B)(B\A). (A  B) \ (A  B)  ⁽¹⁰⁾ (A  B)  (AB)  ⁽⁹⁾ (A  B)  (A B)  ⁽⁴⁾  ((A  B) A)  ((A  B) B)  ⁽⁴⁾  ((A A)  (B A))  ((A B)  (B B))  ⁽⁷⁾  (  (BA))  ((AB)  ) = ⁽⁵⁾ (BA)  (A B) = ⁽¹⁰⁾ (B \ A)  (A \ B).

Принцип двойственности.

Принцип двойственности состоит в том, что из любого равенства, относящегося к системе подмножеств фиксированного множества U, автоматически может быть получено другое, двойственное, равенство, путем замены всех рассматриваемых множеств их дополнениями, объединений множеств – пересечениями, пересечений множеств – объединениями.

3. Отношения на множествах

Рассмотрение «жизненного», точнее, «программистского», примера. Пусть есть три множества: D – данных, P – программ и R – результатов. Для  программы возможны отношения: данные для этой программы, результаты работы этой программы, и т.п. Набору данных можно сопоставить множество программ, которые могут с этими данными работать…

Перейдем к формализации понятия «отношения».

1. Прямое произведение множеств

Упорядоченная последовательность, содержащая n элементов некоторого множества, называется n-кой, или набором из n элементов. Обычно n-ка, образованная последовательностью a₁, a₂,…, a_n обозначается (a₁, a₂,…, a_n). При малых n говорят о двойках элементов, тройках и т.д.

• Согласно этому определению, один и тот же элемент может встречаться в n-ке несколько раз. Кроме того, поскольку n-ка является упорядоченной последовательностью, две n-ки, составленные из одних и тех же элементов, но в разном порядке, является различными.

7. Для множества чисел А = {1, 2, 3, 4} можно рассмотреть тройки: (1, 2, 2), (3, 4, 1), (2, 1, 2), причем первая и последняя тройки различны, несмотря на их одинаковый состав.

Прямым (или декартовым) произведением множеств А₁, А₂, …, А_n называется множество всех упорядоченных наборов (x₁ ,x₂, … x_n) таких, что x_i  A_i при  i = 1, 2, …, n. Декартово произведение обозначается А₁  А₂ … А_n. Если одним из сомножителей является пустое множество, то и произведение является пустым множеством.

С тепенью множества A называется его прямое произведение само на себя n раз; обозначается Aⁿ.

8. Рассмотрим два множества: чисел Q = {1, 2, 3, 4, 5, 6, 7, 8} и букв: P = {a, b, c, d, e, f, g, h}. Тогда если рассмотреть произведение PQ, то оно будет иметь вид упорядоченных пар: (a1), …, (a8), (b1), …, (b8), …, (h1), …, (h8). Мощность такого произведения равна 88=64, а сами элементы – клетки шахматной доски.

Пример для общего развития: Пусть имеются множества A={1,2}, B={2,3,4}. Тогда А  B = {(1,2), (1,3), (1,4), (2,2), (2,3), (2,4)}. Если рассмотреть A³={(1,1,1), (1,1,2), (1,2,1), (1,2,2),(2,1,1), (2,1,2),  (2,2,1), (2,2,2)}.

• Точка на плоскости может быть задана упорядоченной парой координат, т.е. двумя точками на координатных осях. Т.о., R² = RR. Метод координат был введен в употребление Рене Декартом, отсюда и название «декартово произведение».

2. Отношения

N-местным отношением R или N-местным предикатом R на множествах А₁, …, А_n называется любое подмножество прямого произведения А₁ … А_n: R  А₁ … А_n. Элементы a₁, a₂, …, a_n | a_i  A_i при  i = 1, 2, …, n связаны отношением R тогда и только тогда, когда упорядоченный набор (a₁ ,a₂, … a_n)  R.

При N = 1 отношение R является подмножеством множества А₁ и называется унарным отношением или свойством.

Наиболее часто встречается двухместное отношение (N = 2), которое называется бинарным отношением R из множества А в множество В, или соответствием: это подмножество произведения множеств А и В: R  А B.

Если элементы a и b множеств А и В (a,b)R, то говорят, что они находятся в отношении R, для чего часто используется т.н. инфиксная форма записи: aRb. Если R  А A (т.е. А=В), то R называется бинарным отношением на множестве А. Соответственно, отношение R  А ⁿ называется N-местным предикатом на множестве А.

Бинарное отношение можно задать указанием всех пар, для которых это отношение выполняется, или графически. Способы графического представления также могут быть различными. Рассмотрим варианты (см. рис.):

1. О 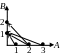снову графического представления бинарного отношения составляет прямоугольная система координат, где по одной оси отмечаются точки (a), представляющие элементы множества А, а по другой – точки (b), представляющие элементы множества В. Тогда точки с координатами (a,b) обозначают элементы декартова произведения.

2. На той же прямоугольной системе координат отношения для  пары (a,b) показаны стрелками из a в b.

3. М ножества A и B показаны точками на параллельных линиях, а отношения между ними – стрелками, направленными от a к b.

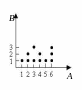9. Р ассмотрим множества A={1,2,3,4,5,6}, B={1,2,3}. Определим на этих множествах отношение RAB: R = {(x,y) | x делится на y}. R можно представить графически так, как это показано на рисунке справа. Кроме того, можно задать это же отношение множеством упорядоченных пар: {(1,1), (2,1), (2,2), (3,1), (3,3),(4,1),  (4,2), (5,1), (6,1), (6,2), (6,3)}, которые соответствуют тем же точкам на плоскости.

Определим несколько отношений, необходимых при рассмотрении множеств.

Пусть R есть отношение на множестве A: R  А A, a,b  A. Тогда:

О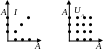 братное отношение: R^–1 = {(b,a) | (a,b)  R}.

Дополнение отношения: R = {(a,b) | (a,b)R}.

Тождественное отношение, или диагональ: I_А = {(a,a) | a  A}.

У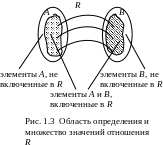 ниверсальное (или полное) отношение: U_A = {(a,b) | a  A и b  A}.

Свяжем с каждым бинарным отношением R между множествами A и B два множества – область определения _R и множество (или область) значений _R. Они определяются следующим образом:

_R = {x| (x,y)R для некоторого y},

_R = {y| (x,y)R для некоторого x}.

10. (в практике) Пусть на множестве A = {1,2,3,4,5} задано отношение R: R = {(x,y) | остаток от деления y на x равен 1}. Тогда R = {(5,1),(4,1),(3,1),(2,1),(2,3),(3,4),(2,5),(4,5)}, _R = {2,3,4,5}, _R = {1,3,4,5}.

Образом множества X относительно предиката R называется множество R(X) = {y | (x,y)R для некоторого xX}

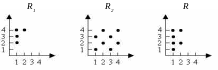
Пусть имеются множества A, B, C и отношения R₁  AB, R₂  BC. Определим отношение R  AC следующим образом: оно действует из A в B посредством R₁, а затем из B в C посредством R₂. Такое отношение называется составным (композицией), или произведением отношений и обозначается R = R₁◦R₂: R = {(x,y) |  z  B, для которого выполнено (x,z)  R₁, (z,y)  R₂}.!!!

11. ( включен в практ.) Пусть A={1,2,3,4}, на множестве A определим два отношения: R₁ = {(x,y) | 2x  y} и R₂ = {(x,y) | x+3y кратно 2}. Найдем графические представления отношений R₁, R₂, R = R₂ ◦R₁ Найдем области определения и области значений для всех отношений. (R₁)={1,2}, (R₁)={2,3,4}, (R₂)={1,2,3,4}, (R₂)={1,2,3,4}, (R)={1,2}, (R)={1,2,3,4}.

Если записать эти же отношения в виде пар, то получим: R₁ = {(1,2),(1,3),(1,4),(2,4)} и R₂ = {(1,1),(1,3),(2,2),(2,4),(3,1),(3,3),(4,2),(4,4)}. Тогда композиция отношений R: (1,2),(2,2)(1,2); (1,2),(2,4)(1,4) и т.п. R = R₁◦R₂ = {(1,2),(1,4),(1,1),(1,3),(1,2),(1,4),(2,2),(2,4)}. Устранив повторяющиеся элементы, получим: R = {(1,2),(1,4),(1,1),(1,3),(2,2),(2,4)}.

П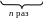 усть R – бинарное отношение на множестве A. Степенью отношения R на множестве A называется его композиция с самим собой. Rⁿ=R◦R◦…◦R.

3. Свойства отношений

Теорема 1.1: Для любых бинарных отношений P, Q, R выполняются следующие свойства:

1. (P^–1)^–1=P; 2. (P◦Q)^–1= Q^–1◦P^–1; 3. (P◦Q)◦R=P◦(Q◦R) (ассоциативность композиции).

Доказательство:

1. По определению обратного отношения условие (x,y)P равносильно условию (y,x)P^–1, что выполняется  когда (x,y)(P^–1) ^–1.

2. Пусть (x,y)(P◦Q)^–1, тогда (y,x)(P◦Q)   z | (y,z)Q и (z,x)P. Тогда (x,z)P^–1, (z,y)Q^–1  (x,y)Q^–1◦P^–1. Обратное включение аналогично.

3. Пусть (x,y)(P◦Q)◦R, тогда, по определению,  u, v | (x,u)R, (u,v)Q, (v,y) P. Это равносильно тому, что (x,u)R, (u,y)P◦Q.

В силу свойства ассоциативности обычно композицию отношений обозначают (P◦Q)◦R  PQR.

лекция 3(24.02.05)

Бинарное отношение R на множестве А называется рефлексивным, если для любого его элемента a выполняется aRa: a   aRa.

Бинарное отношение R на множестве А называется антирефлексивным, если для любых его элементов a,b aRb  a  b.

Бинарное отношение R на множестве А называется симметричным, если из его выполнения для a, b следует выполнение для b, a:  a, b   aRb  bRa.

Бинарное отношение R на множестве А называется антисимметричным, если из его выполнения для a, b и b, a следует, что a и b совпадают.  a, b   aRb и bRa  a = b.

Бинарное отношение R на множестве А называется транзитивным, если из его выполнения для a,b и для b,c следует его выполнение для a,c:  a, b, c   aRb и bRc  aRc.

Бинарное отношение R на множестве А называется полным, или линейным, если для любых двух различных элементов множества A оно выполняется или для a, b, или для b, a:  a, b   | ab  aRb или bRa.

12. Рассмотрим отношение R на множестве натуральных чисел следующим образом: R = {(x,y) | x – делитель y}. Это отношение является рефлексивным, т.к. x/x =1 x  N Отношение R антисимметрично, т.к. если x/y  N и y/x  N , то x = y. Проверим транзитивность R. y/x  N и z/y  N  z/x = z/y  y/x  N.

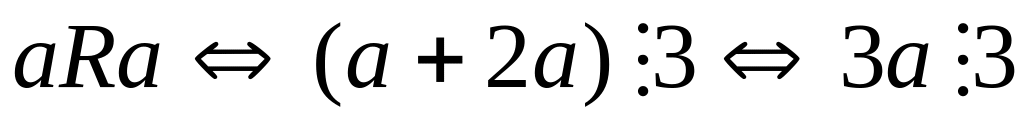
13. (Включен в практ. задачи) Определим отношение R на множестве натуральных чисел: (a+2b делится на 3). Это отношение является рефлексивным, т.к.  Отношение R симметрично. 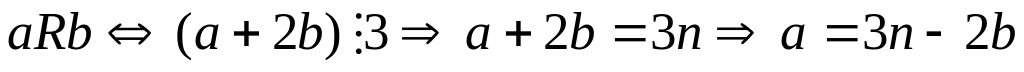. Для того, чтобы проверить выполнение bRa, необходимо показать, что 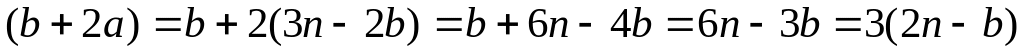, 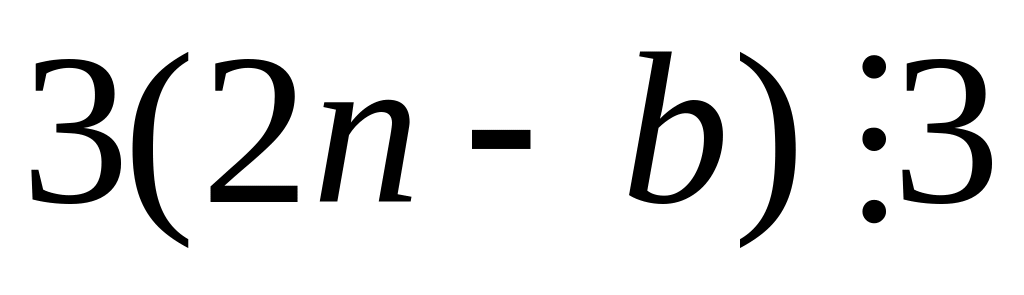 bRa выполнено. Проверим, что R – транзитивно. ,  a+2b = 3n  a=3n–2b. 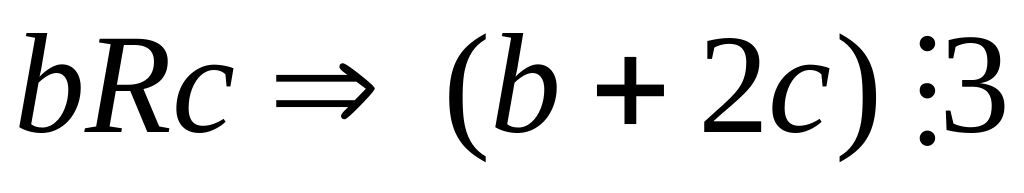.  b+2c = 3m  2c=3m–b. Для того, чтобы проверить выполнение aRc, необходимо показать, что 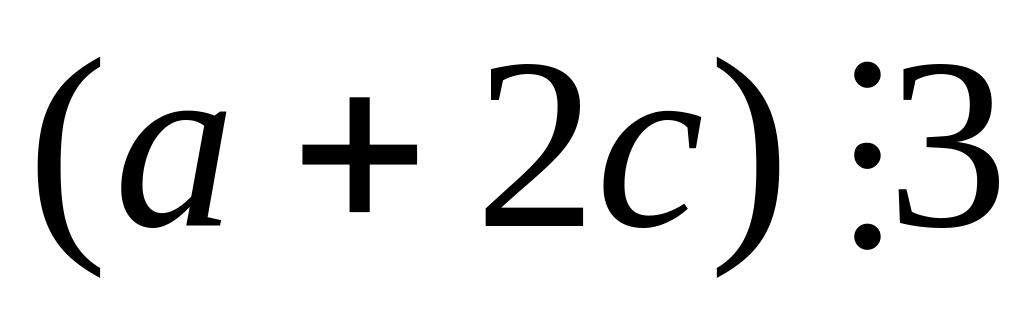. 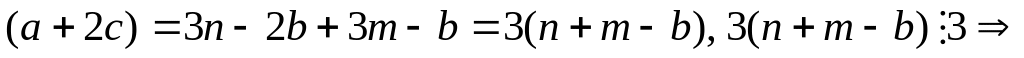aRc выполнено. 

Теорема 1.2 (о проверке свойств отношения):

Отношение R на множестве A²:

1. R рефлексивно  I  r;

2. R симметрично  R = R^–1;

3. R транзитивно  r◦r  r;

4. R антисимметрично  r  r–1  I;

5. R полно  R  I  R^–1 = U;

Доказательство:

1.  R рефлексивно  aA выполняется aRa, т.е. (a,a)R. Но множество всех таких a составляет I  IR.  IR  aA {(a,a)}=I  (a,a)R, т.е. R рефлексивно.

2.  R симметрично  a,bA | (a,b)R  (b,a)R. Но если (a,b)R  (b,a)R^–1 по определению обратного отношения. Поскольку это справедливо для любых a,b, то R  R^–1 и R^–1  R  R^–1 = R.  R^–1 = R  RR^–1 и R^–1R  a,bA | (a,b)R  (a,b)R^–1 и (a,b)R^–1  (a,b)R. Если (a,b)R, то по определению (b,a)R^–1, значит, (b,a)R, т.е. a,bA | (a,b)R (b,a)R, что и означает симметричность.

3.  R транзитивно  a,b,cA | (a,b)R и (b,c)R  (a,c)R. Но по определению композиции R◦R {(a,b) |  cA | (a,c)R и (c,b)R}  по определению транзитивности, эта пара (a,b)R, т.е. R◦RR.  Если R◦RR, то это значит, что a,bA | (a,b)R◦R эта пара (a,b)R. По определению композиции, R◦R {(a,b) |  cA | (a,c)R и (c,b)R}, но было показано, что (a,b)R,  R транзитивно.

4.  От противного. Пусть R  R^–1  I. Значит,  ab| (a,b)R и (a,b)R^–1, т.е. в пересечении существует общий элемент (a,b). Но если (a,b)R^–1, то (b,a)R. Получили, что  ab | (a,b)R и (b,a)R. По условию, R антисимметрично  a,bA | (a,b)R и (b,a)R  a=b. Получено противоречие:  ab … a=b.  R  R^–1  I  (a,bA | (a,b)R и (a,b)R^–1  (a,b)I  a=b). Но (a,b)R^–1(b,a)R  ((a,b)R и (b,a)R  a=b)  антисимметричность.

5. Доказать самостоятельно. 

4. Представление отношений в ЭВМ

Удобным способом представления отношений в ЭВМ является матричная форма. Рассмотрим два конечных множества A={a₁,a₂,…,a_m}, B={b₁,b₂,…,b_n} и бинарное отношение P  AB . Определим матрицу [P] = (p_ij) бинарного отношения P по следующему правилу: Полученная матрица содержит полную информацию о связях между элементами и позволяет представлять эту информацию на компьютере.

• Заметим, что любая матрица, состоящая из нулей и единиц, является матрицей некоторого бинарного отношения.

14. Р ассмотрим отношение P на множестве A², где A={1,2,3} (см. иллюстрацию). Матрица этого отношения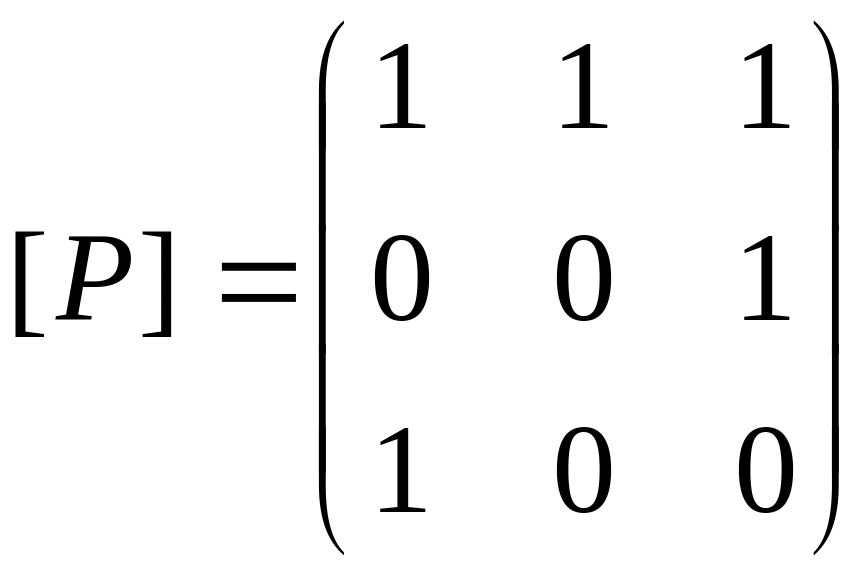

Основные свойства матриц бинарных отношений:

1. Если бинарные отношения P,Q  AB, [P] =(p_ij), [Q] = (q_ij), то [PQ] = (p_ij+q_ij), [PQ] = (p_ij·q_ij), где умножение осуществляется обычным образом, а сложение – по логическим формулам (т.е. 0+0=0, во всех остальных случаях 1). Итак: [PQ] = [P]+[Q], [PQ] = [P]*[Q].

15. Пусть отношения P и Q заданы: 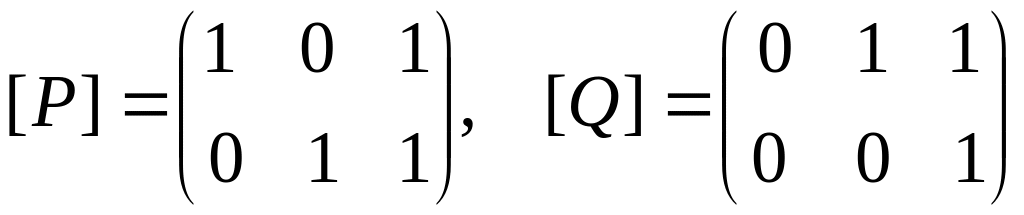. Тогда матрица их суммы [PQ] = [P]+[Q] =  , матрица произведения: [PQ] = [P]*[Q] =  .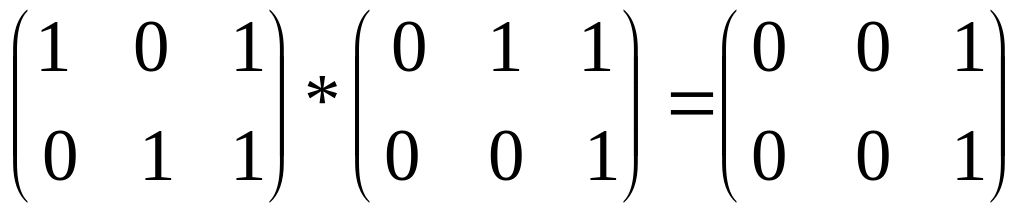

2. Если бинарные отношения P  AB, Q  BC, то [P◦Q] = [P]·[Q] , где умножение матриц [P] и [Q] осуществляется по обычному правилу, а произведение и сумма элементов из [P] и [Q] – по правилам пункта 1.

3. Матрица обратного отношения P^–1 равна транспонированной матрице отношения P: [P^–1]=[P]^T.

4. Если PQ, [P]=(p_ij), [Q]=(q_ij), то p_ij  q_ij. i,j.

5. Матрица тождественного отношения единична: [I_A] = (I_ij) :  I_ij =1  i=j.

6. Пусть R – бинарное отношение на A². Отношение R называется рефлексивным, если xA (x,x)R, т.е. I_AR (на главной диагонали R стоят единицы). Отношение R называется симметричным, если x,yA (x,y)R  (y,x)R, т.е. R^–1=R, или [R]=[R]^T (матрица симметрична относительно главной диагонали). Отношение R называется антисимметричным, если R R^–1 I_A, т.е. в матрице [R R^–1]=[R]*[R]^T вне главной диагонали все элементы равны 0. Отношение R наз. транзитивным, если (x,y)R, (y,z)R (x,z)R, т.е. R◦RR.

16. Пусть отношение P на множестве A², где A={1,2,3}, задано матрицей 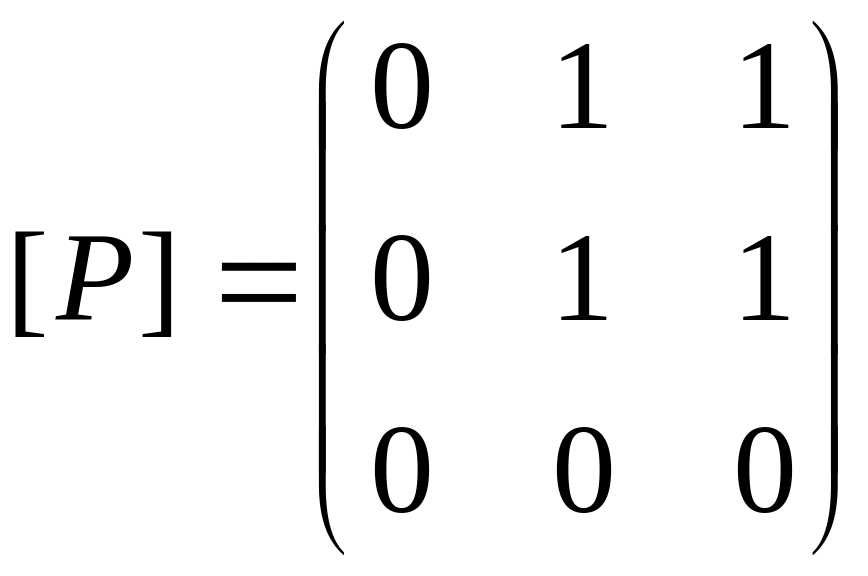. Поскольку на главной диагонали есть нулевые элементы, отношение не рефлексивно. Поскольку матрица не симметрична, отношение тоже не является симметричным. Проверим его антисимметричность, для чего возьмем транспонированную матрицу и вычислим [PP^–1] = [P]*[P]^T = . Все элементы вне главной диагонали равны 0,  отношение антисимметрично. Проверим транзитивность: [P◦P] = [P]? [P◦P] = 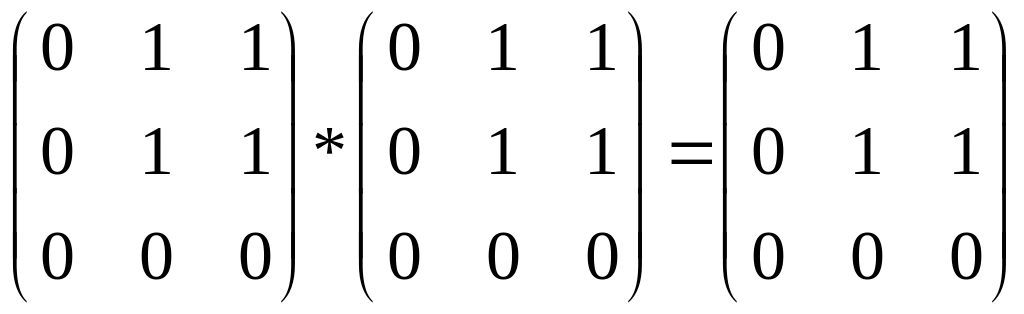  отношение транзитивно.

5. Отношение эквивалентности

Бинарное отношение R на множестве А называется отношением эквивалентности, если оно является рефлексивным, симметричным и транзитивным. Обычно отношение эквивалентности обозначают через  или ~.

17. 1. Отношения равенства чисел и множеств, равномощности множеств являются отношениями эквивалентности. 2. Отношение подобия на множестве треугольников является тривиальным отношением эквивалентности. 3. Отношение эквивалентности – на множестве программ: {(a,b) | программы a, b вычисляют одну и ту же функцию на определенной машине}.

Пусть R – отношение эквивалентности на множестве А. Определим класс эквивалентности [x] для xA: [x] = {y | xRy}, т.е. это множество всех элементов A, которые R-эквивалентны x.

Пусть E – эквивалентность на множестве M. Тогда семейство классов эквивалентности множества M называется фактормножеством множества M по отношению E и обозначается M /E ={E(x)| xM}.

18. Для отношения принадлежности к одной студенческой группе классом эквивалентности является множество студентов одной группы. Тогда фактормножество множества всех студентов СибГУТИ по этому отношению эквивалентности представляет собой множество всех студ. групп СибГУТИ.

Утверждение 1.1. Всякое отношение эквивалентности на множестве M определяет разбиение множества M, причем среди элементов разбиения нет пустых; и обратно, всякое разбиение множества M, не содержащее пустых элементов, определяет отношение эквивалентности на множестве M:

  M²   ß= {B_i | B_i  M, B_i  , M = B_i и  i,j ij  B_iB_j=}.

6. Отношение порядка

Бинарное отношение R на множестве А называется отношением порядка, если оно антисимметрично и транзитивно. Отношение порядка может быть рефлексивным, и тогда оно называется отношением нестрогого порядка (обычно обозначается ). Если отношение порядка антирефлексивно, то оно называется отношением строгого порядка и обозначается обычно <. Отношение порядка может быть полным (линейным), и тогда оно называется отношением линейного порядка (если любые два элемента сравнимы между собой), а множество – вполне упорядоченным. Если отношение порядка не обладает свойством полноты, то оно называется отношением частичного порядка, а множество с заданным на нем отношением частичного порядка называется частично упорядоченным множеством. Обычно отношение порядка в общем случае обозначают <, и вместо aRb или (a,b)  R пишут a<b. Для отношения < обратным является >.

19. 1. Свойство «быть ровесником» можно считать отношением эквивалентности на множестве всех студентов 1-го курса СибГУТИ. Свойство «быть старше» является отношением частичного порядка на множестве всех студентов института. 2. Отношение < на множестве чисел является отношением строгого полного порядка, отношение  – нестрогого полного порядка. Следовательно, множество чисел является линейно упорядоченным. Отношение  на булеане P(M) является отношением нестрого частичного порядка. 3. Отношение подчиненности на предприятии является отношением частичного порядка – сотрудники разных лабораторий несравнимы.

Пусть дано ч.у.м. M с отношением порядка : Ữ= {M,}. Тогда: Элемент a ч.у.м. Ữ называется максимальным, если yM | ay  a=y; или если во всем множестве нет элемента, большего чем a. Элемент a называется минимальным, если yM | y a  a=y (т.е. во всем множестве нет элемента меньшего чем a).

Элемент b ч.у.м. Ữ называется наибольшим, если x  b xM (т.е. любой другой элемент множества меньше либо равен b). Элемент b называется наименьшим, если b  x xM (т.е. любой другой элемент множества больше либо равен b). Наибольший (наименьший) элемент ч.у.м. Ữ обычно обозначают max Ữ (min Ữ).

Наибольший (наименьший) элемент обычно называют единицей, а наименьший – нулем множества M.

• Заметим, что всякий наибольший элемент (если он существует) является максимальным, а всякий наименьший – минимальным. Обратное утверждение неверно. Максимальных (минимальных) элементов может быть несколько.

20. 1. Пустое множество является минимальным элементом булеана по включению. 2. Пусть ч.у.м. A содержит три элемента, условно обозначенные 1, 2 и 3 (см. рисунок). Отношение порядка задано парами: 11, 12, 22, 32, 33 (показано стрелками). Видно, что элемент 2 является наибольшим, а элементы 1 и 3 – минимальными, но не наименьшими, т.к. они не сравнимы между собой.

Д ля ч.у.м. M с отношением порядка  и подмножеством AM элемент aM называется верхней гранью множества A, если xA x  a. Элемент aM называется точной верхней гранью множества A и обозначается sup A, если a является верхней гранью и для любого другого элемента a’, являющегося верхней гранью, верно a  a’. Наибольший элемент множества A, если он существует, является sup A.

Аналогично, элемент bM называется нижней гранью множества A, если yA b y. Элемент bM называется точной нижней гранью множества A и обозначается inf A, если b является нижней гранью и для любого другого элемента b’, являющегося нижней гранью, верно b’ b. Наименьший элемент множества A, если он существует, является inf A.

лекция 4(03.03.05)

Утверждение 1.2. Во всяком конечном непустом частично упорядоченном множестве существует минимальный элемент.

Замкнутость множества означает, что многократное повторение допустимых шагов не выводит за пределы этого множества.

Пусть R и R’ – отношения на множестве M. Тогда отношение R’ называется замыканием отношения R относительно свойства С, если:

1. R’ обладает свойством С: С(R’);

2. R’ является надмножеством R: R  R’;

3. R’ является наименьшим: С(R’’), R  R’’  R’  R’’.

21. Множество четных натуральных чисел замкнуто относительно операций сложения и умножения, но не замкнуто относительно операций вычитания и деления.

Пусть A – вполне упорядоченное множество с отношением порядка . Введем отношение  на множестве упорядоченных наборов из A следующим образом:

(a₁,…,a_m)  (b₁,…,b_n)  m  n и i = 1,..,m a_i= b_i или  k  min(n,m) | a_k  b_k и a_i= b_i i < k, т.е. первые элементы совпадают, а k-й меньше.

Такое отношение называется лексикографическим, или алфавитным порядком.

4. Функции

   1. Определение функции

Бинарное отношение R между множествами А и B называется однозначным, если из его выполнения для a, b и a, c (aA, b,cB) следует, что b и c совпадают.  a  , b,cB aRb и aRc  b = c (одному элементу множества A не могут соответствовать разные элементы, находящиеся с ним в отношении R).

О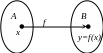 днозначное отношение f между множествами А и B, заданное для каждого элемента множества A, называется отображением множества A в множество B, или функцией из A в B: f : A  B.

Дадим формальное определение.

Отношение f между элементами множеств A и B называется функцией из A в B и обозначается f : A  B, если оно обладает следующими двумя свойствами:

а) xA  y  B | (x,y)f; б) если (x, y)  f и (x, z)  f  y = z.

Для функции f обычно вместо записи (x,y)  f используется т.н. префиксная форма: y = f(x). При этом x называется аргументом, а y – значением функции f.

Для f : A  B область определения Dom(f)  {x  A |  y B | y = f(x)}, область значений Codom(f)  {y  B |  x A | y = f(x)}.

Если Dom(f) =A, то функция называется тотальной, а если Dom(f)  A – частичной. Сужением функции f : A  B на множество M  A называется функция f |_M, определяемая следующим образом: f |_M  {(x,y) |  y = f(x), xM}.

Для тотальной функции ее сужение на множество Dom(f) совпадает с самой функцией f.

Для f : A  B и x  A: если y = f(x), то y называется образом элемента x, а x – прообразом элемента y. Для любого непустого подмножества C  A его образом относительно f называется множество f(C) = {f(x) | xC}.

Функция f:A₁A₂…A_nB называется функцией n аргументов, или n-местной функцией.

2. Классификация функций

Отображение f : A  B называется (см. рисунок ниже):

• инъективным (инъекцией), если любым различным значениям аргумента соответствуют различные значения функции: f(x₁) = f(x₂)  x₁ = x₂;

• сюръективным, сюръекцией, или отображением на, если любому элементу y множества B соответствует элемент x множества A, такой, что f(x) = y: yB  xA | f(x) = y;

• биективным, биекцией, или взаимно однозначным соответствием, если оно является одновременно инъекцией и сюръекцией;

• п 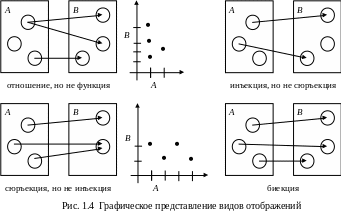ерестановкой множества A, если A = B и функция f : A  A является взаимно однозначным соответствием.

Если функция I : A  A определена как I(a)=a aA, то I называется тождественной функцией на множестве A.

Множество называется счетным, если его элементы можно пронумеровать, т.е. если существует взаимно однозначное соответствие между элементами этого множества и множеством натуральных чисел.

22. Всякое конечное множество счетно. Множество четных натуральных чисел счетно.

Утверждение 1.4. 1. Всякое подмножество счетного множества конечно или счетно. 2. Сумма любого конечного или счетного числа счетных множеств есть счетное множество.

Обратное отношение f^–1, которое определялось ранее, может не быть функцией, даже если f является функцией из A в B. Если обратное отношение f^–1 является функцией, то ее называют обращением функции, или обратной функцией.

Теорема 1.3 (об обратной функции):

Если функция f : A  B является биекцией, то обратное отношение f^–1 также является функцией из B в A, причем биекцией. Обратно, если f^–1 – функция из B в A, то f является биекцией.

Доказательство:

 Для доказательства того, что  f^–1– функция из B в A, нужно убедиться, что областью определения  f^–1 является B, и что если (b,a)  f^–1 и (b,a’)  f^–1, то a = a’. Поскольку f сюръективна (т.е. отображение на), то bB  aA | f(a)=b. Значит, (b,a)  f^–1, и B является областью определения f^–1. Пусть теперь (b,a)  f^–1 и (b,a’)  f^–1, тогда (a,b) и (a’,b) принадлежат f. Поскольку f инъективна, то a=a’. Значит, f^–1– функция.

Теперь покажем, что она является биекцией, т.е. сюръективна и инъективна.

Поскольку f – функция, то aA  bB| f(a)=b, т.е. (a,b)f. Тогда (b,a) f^–1, и элемент a принадлежит области значений функции f^–1. Значит, A представляет собой область значений f^–1, и сама функция f^–1 сюръективна. Для доказательства инъективности возьмем (b,a)  f^–1 и (b’,a)  f^–1, т.е. a = f^–1(b) и a = f^–1(b’). Тогда

f(a) = b  и f(a) = b’  b’= b, т.к. f – функция.

 Для доказательства обратного утверждения нужно провести аналогичные рассуждения, заменив f^–1 на f. 

Теорема 1.4: Если функция f : A  B является биекцией, то:

а)  b B f(f^–1(b))=b, б)  a A f^–1(f(a))=a.

Доказательство: Возьмем  b  B. Поскольку f – биекция, то  aA | a= f^–1(b). Тогда f(a)=b. Но поскольку a = f^–1(b),  f(f^–1(b)) = f(a) = b 

Доказательство второго утверждения выполняется аналогично.

Теорема 1.5: Если функция f : A  A и I – тождественная функция на A, то I◦ f = f  ◦ I = f. Если для f существует обратная функция, то f^–1◦ f = f ◦ f^–1= I.

Ядро функции обозначается ker f  =  f ◦ f^–1.

Утверждение 1.5. Ядро функции является отношением эквивалентности на области определения функции.

Теорема 1.6: Пусть функции g : A  B и f : B  C. Тогда: