
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник
.pdf
Доказательство. Из условия дифференцируемости |
функции |
следует, |
что |
|||||||
lim ∆z = 0 , и поэтому дифференцируемая функция непрерывна в точке |
M . |
|||||||||
∆x→0 |
|
|
|
|
|
|
|
|
|
|
∆y→0 |
|
|
|
|
|
|
|
|
|
|
Частное приращение по переменной х имеет |
вид |
∆x z = A∆x + α∆x , где |
α- |
|||||||
бесконечно малая величина, зависящая от ∆x , причем α → 0 при ∆x → 0 . |
|
|||||||||
Аналогично, |
частное |
приращение по |
переменной |
у |
имеет |
вид |
||||
∆y z = B∆y +β∆y , |
где β - бесконечно малая величина, |
зависящая от ∆y , причем |
||||||||
β → 0 при ∆y → 0 . Имеем |
|
|
|
|
|
|
|
|
||
|
lim |
∆x z = A и lim |
∆y z |
= B , т.е. |
∂z = A и ∂z |
= B . |
|
|||
|
|
|
||||||||
|
∆x→0 |
∆x |
∆y→0 |
∆y |
∂x |
∂y |
|
|
|
|
Теорема доказана.
Следствие 2.1. Условие дифференцируемости функции (2.1) можно представить в виде
∆z = ∂∂xz ∆x + ∂∂yz ∆y + γ ,
где γ = α ∆x + β ∆y = o(ρ) - бесконечно малая величина при ∆x → 0 и ∆y → 0 . Здесь o - «о малое» (см. раздел I §3.7), ρ = 
 ∆x2 + ∆y2 .
∆x2 + ∆y2 .
Формула для вычисления полного дифференциала вытекает из равенств
(2.3):
dz = |
∂z dx + |
∂z dy . |
(2.4) |
|
∂x |
∂y |
|
Заметим, что из непрерывности функции и существования частных производных еще не следует дифференцируемость функции.
Например, функция z = 3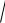 xy в точке O(0;0) непрерывна и имеет частные
xy в точке O(0;0) непрерывна и имеет частные
производные, но не дифференцируема в этой точке. В самом деле, непрерывность функции в начале координат вытекает из равенства
lim 3 xy = 0 = f (0,0). Вычислим частные производные этой функции в этой
x→0 y→0
точке. По определению |
fx′(0,0) = lim |
f (x,0) − f (0,0) |
= lim |
0 |
= 0 ; |
||||
|
x |
||||||||
|
|
x→0 |
x |
|
|
x→0 |
|
||
f y′(0,0) = lim |
|
f (0, y) − f (0,0) |
= lim |
0 |
= 0 . |
|
|
|
|
|
y |
y |
|
|
|
||||
y→0 |
|
y→0 |
|
|
|
|
|||
Обе частных производных в точке O(0;0) равны 0. Исследуем теперь функцию
на дифференцируемость. Для этого проверим, можно ли приращение функции в точке (0,0) представить в виде
f (x, y) − f (0,0) = fx′(0,0)x + f y′(0,0) y + α(x) x + β( y) y ,
где α(x) и β( y) - бесконечно малые величины для, соответственно, x и y, стремящихся к нулю. В нашем случае эта формула будет иметь вид
121

3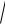 xy = α(x) x + β( y) y = o (
xy = α(x) x + β( y) y = o (
 x2 + y2 ).
x2 + y2 ).
Проверим, справедливо ли это утверждение. Для этого рассмотрим предел
lim |
|
|
3 |
xy |
|
|
|
|
. |
Покажем, |
что он |
|
|
не равен нулю. В самом деле, |
если при |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x→0 |
x |
2 |
+ y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
вычислении |
|
|
|
|
|
|
предела |
|
|
|
|
|
положим |
x = y , |
то |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x23 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|||||
lim |
|
|
|
3 |
xy |
|
|
|
|
= lim |
|
= |
|
lim |
|
|
|
= ∞ . Следовательно, |
рассматриваемый |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||||
x→0 |
x |
2 |
+ y |
2 |
|
|
|
x→0 |
|
2 x |
2 |
|
x→0 |
x |
|
|
||||||||||||||
y→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
предел не существует, и, таким образом, 3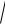 xy ≠ o(
xy ≠ o(
 x2 + y2 ) при (x; y ) → (0; 0) ,
x2 + y2 ) при (x; y ) → (0; 0) ,
то есть функция z = 3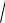 xy в точке O(0;0) не дифференцируема.
xy в точке O(0;0) не дифференцируема.
Достаточные условия дифференцируемости функции даны в следующей теореме, которую мы приведем без доказательства.
Теорема 2.2. Если функция z = f (x, y ) имеет непрерывные частные производные z′x и z′y в точке M (x; y ) , то она дифференцируема в этой точке и её полный дифференциал выражается формулой (2.4).
Дифференциал dz функции двух переменных z = f (x, y) обладает теми же свойствами, что и дифференциал функции одной переменной:
1)d (c z) = c dz , где c = con st ,
2)d (u + v) = du + dv ,
3)d (uv) = u dv + v du ,
u |
v du − u dv |
|
|
|
|
|
|
|||
4) d |
|
= |
|
|
. |
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|||
v |
|
|
|
|
|
|
|
|||
Доказательство приведем для свойства 3). |
|
|
|
|
||||||
Пусть w = uv |
и dw = |
∂w du + |
∂w dv , но |
∂w |
= v , |
∂w |
= u . Тогда получим |
|||
|
|
|
|
|
∂u |
∂v |
∂u |
|
∂v |
|
dw = d (uv) = v du + u dv .
Полный дифференциал функции нескольких переменных обладает, как и в одномерном случае, свойством инвариантности формы. Это будет доказано в следующем параграфе.
§2.3. Дифференцирование сложной функции и неявной функции
Пусть z = f (x, y) - функция двух переменных, каждая из которых является функцией независимой переменной t, то есть x = x(t) , y = y(t) . В этом случае функция z = f (x(t), y(t)) является сложной функцией одной независимой переменной t , а переменные х и у - промежуточные переменные.
122

Теорема 2.3. Если z = f (x; y) - дифференцируемая в точке M (x; y) D функция и x = x(t) и y = y(t) – дифференцируемые функции независимой переменной t , то производная сложной функции z = f (x(t), y(t)) вычисляется по формуле
|
dz |
= ∂z |
|
dx |
+ ∂z |
|
dy |
(2.5) |
|
dt |
dt |
dt |
|||||
|
∂x |
|
∂y |
|
t приращение ∆t . Тогда |
|||
Доказательство. Дадим независимой переменной |
||||||||
функции x = x(t) и y = y(t) получат приращение ∆x |
и ∆y соответственно. Они, |
|||||||
в свою очередь, вызовут приращение ∆z функции z. |
||||||||
Так как по условию функция z = f (x, y) |
дифференцируема в точке M (x; y) , |
|||||||
то ее полное приращение можно представить в виде |
|
|||||||
∆z = ∂z ∆x + ∂z ∆y + α∆x + β∆y , |
||||||||
∂x |
∂y |
|
|
|
|
|||
где α→0, β→0 |
при ∆x →0, ∆y →0. |
|||||
перейдем к |
пределу при |
∆t → 0 . |
||||
непрерывности |
функции |
x = x(t) |
и |
|||
дифференцируемые). Получаем: |
|
|||||
lim |
∆z = ∂z |
lim |
∆x |
+ ∂z lim |
||
∆t→0 |
∆t |
∂t |
∆t→0 |
∆t |
∂y |
∆t→0 |
Разделим выражение ∆z |
на ∆t и |
||||||
Тогда |
∆x → 0 |
и |
∆y → 0 |
в |
силу |
||
y = y(t) |
(по условию теоремы |
они |
|||||
∆y |
+ lim α lim |
∆x + lim β lim |
∆y |
, |
|||
∆t |
∆t→0 |
∆t→0 |
∆t |
∆t→0 |
∆t→0 |
∆t |
|
т.е.
dzdt = ∂∂xz dxdt + ∂∂xz dydt + 0 dxdt + 0 dydt ,
или |
|
|
|
|
|
dz |
|
∂z |
|
dx |
|
∂z |
|
|
|
dy |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
+ |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||
Теорема доказана. |
|
|
|
|
|
dt |
∂x |
dt |
∂x |
dt |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следствие 2.2. Пусть z = f (x, y), |
где |
y =y(x), |
|
|
т.е. |
z = f (x, y(x)) |
- |
сложная |
|||||||||||||||||||||||||||||
функция одной независимой |
переменной |
x . Тогда |
производную |
dz |
можно |
||||||||||||||||||||||||||||||||
dx |
|||||||||||||||||||||||||||||||||||||
найти по формуле, называемой формулой полной производной, |
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dz = |
∂z + ∂z dy |
|
|
|
|
|
|
|
(2.6) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
∂x |
∂y |
|
|
dx |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
играет x . Согласно |
||||||||||||||||||||||
Доказательство. В данном случае роль переменной |
|||||||||||||||||||||||||||||||||||||
формуле (2.5) имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
∂z |
|
∂z |
|
dy |
|
|
||||||||||
|
dz |
∂z |
|
dx |
|
|
|
∂z |
|
|
|
dy |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
= |
|
|
|
|
+ |
|
|
|
|
или |
|
|
= |
|
+ |
|
|
|
, |
|
|
||||||||||||||
|
dx |
∂x |
dx |
|
∂y |
dx |
|
|
dx |
∂x |
∂y |
dx |
|
|
|||||||||||||||||||||||
что и требовалось доказать.
Пусть z = f (x, y), где x = x(u, v), y = y(u, v) . Тогда z = f (x(u,v), y(u,v)) - сложная функция независимых переменных u и v. Ее частные производные
123

∂z |
и |
∂z |
можно найти, используя формулу (2.5) следующим образом. |
|
∂u |
∂v |
|||
|
|
Зафиксировав v, заменяем в
∂z ∂x ∂y
производными ∂u , ∂u , ∂u :
∂z
∂u
Аналогично получаем:
dz dx dy
ней dt , dt , dt соответствующими частными
= |
∂z |
|
∂x |
+ |
∂z |
|
∂y |
(2.7) |
|
∂x |
∂u |
∂y |
∂u |
||||||
|
|
|
|
|
∂z = ∂z ∂x + ∂z ∂y
∂v ∂x ∂v ∂y ∂v .
Таким образом, производная сложной функции (z) по каждой независимой переменной (u и v) равна сумме произведений частных производных этой функции (z) по ее промежуточным переменным (x и y) на их производные по соответствующей независимой переменной (u или v).
Пример 2.8. Найти частные производные |
∂z |
, |
∂z |
, если z = ln(x2 + y2 ), x = u v, y = |
u |
. |
|||||||||
∂u |
∂v |
|
|||||||||||||
Решение. Используем формулу (2.7): |
|
|
|
|
|
|
|
v |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∂z |
= |
|
1 |
|
2x v + |
1 |
2 y |
1 |
. |
|
|
|||
|
|
|
+ y2 |
x2 + y2 |
|
|
|
||||||||
|
∂u x2 |
|
|
|
|
|
v |
||||||||
Преобразуем правую часть полученного равенства:
∂z |
= |
2 |
( x v + |
|
∂u |
x 2 + y 2 |
|||
|
|
Аналогично,
Далее, преобразуем:
y |
|
|
|
2 |
|
|
|
|
|
u |
|
|
|
2v2 |
u (v4 + 1) |
|
2 |
. |
|||||
|
) = |
|
|
|
|
|
|
|
uv v + |
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
v |
|
|
|
u |
2 |
|
u |
2 |
(v |
4 |
+ 1) |
v |
2 |
u |
|||||||||
|
(uv) |
2 |
+ |
|
|
v v |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∂z |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
u |
||
|
= |
|
|
|
|
2 x u + |
|
|
|
|
2 y |
− |
|
|
|
|
|
2 |
+ y |
2 |
x |
2 |
+ y |
2 |
v |
2 |
|||||
∂v x |
|
|
|
|
|
|
|
|
|
||||||
∂z |
|
|
|
2 |
|
|
|
= |
|
|
|
|
x u − |
∂v |
x |
2 |
+ y |
2 |
||
|
|
|
|
=2 v4 −1. v v4 +1
yuv2 =
2
(uv) |
2 |
u 2 |
||
|
+ |
|
|
|
|
|
|||
|
|
v |
||
|
2 |
|
u 2 |
|
|
|
2v 2 |
u 2 (v4 −1) |
|
||||||
u |
|
v − |
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
v |
3 |
u |
2 |
(v |
4 |
+ 1) |
v |
3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Теперь, используя правило дифференцирования сложной функции, покажем, что полный дифференциал обладает свойством инвариантности: полный дифференциал функции z = f (x, y) сохраняет один и тот же вид независимо от того, являются аргументы независимыми переменными или функциями независимых переменных.
Рассмотрим сложную функцию z = f (x, y) , где x = x(u, v), y = y(u, v) , т.е. функцию z = f (x (u,v), y (u, v)) = F (u,v), где u и v - независимые переменные. Найдем полный дифференциал этой функции
124

|
|
|
dz = |
∂F |
du + |
∂F |
dv = |
|
∂z |
du + |
∂z |
dv = |
|
||||||||||||||||
|
|
|
∂u |
∂v |
|
|
∂v |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
|
|
|
|
|
|||||||
|
|
∂z |
|
|
∂x |
|
∂z |
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|||||
= |
|
+ |
|
∂y du + |
|
∂z |
+ |
∂z ∂y |
dv = |
||||||||||||||||||||
|
|
|
|
∂y |
|
|
|||||||||||||||||||||||
|
|
∂x |
∂u |
|
∂u |
|
|
∂x |
∂v |
∂y |
|
∂v |
|
|
|||||||||||||||
|
∂z |
|
|
∂x |
|
|
|
|
∂x |
|
|
∂z |
∂y |
|
|
|
∂x |
|
|
||||||||||
= |
|
|
|
|
|
|
du + |
|
|
dv + |
|
|
|
|
|
|
du + |
|
|
dv . |
|||||||||
∂x |
|
∂u |
∂v |
|
|
|
|
∂u |
∂v |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
||||||||||||||
В последней строке выражения в скобках представляют собой полные |
|||||||||||||||||||||||||||||
дифференциалы dx |
|
и |
|
|
dy |
функций |
x = x(u,v) |
и |
y = y(u, v) . То есть, |
||||||||||||||||||||
справедливо равенство |
|
|
|
|
|
dz = ∂z dx + |
∂z dy . |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, дифференциал сохранил свою форму, хотя смысл дифференциалов dx и dy здесь уже совершенно другой.
Если функция z(x, y) задана неявно уравнением F(x, y, z) =0. |
Оставляя в |
||||
стороне вопрос об условиях существования однозначной функции |
z(x, y) и её |
||||
производных, поставим задачу нахождения частных производных |
∂z |
и |
∂ z |
в |
|
∂x |
∂y |
||||
|
|
|
|||
случае, если они существуют. Подставим в уравнение F(x, y, z) =0 |
вместо z |
||||
функцию z(x, y) . Получим тождество F (x , y , z (x, y )) ≡ 0 . Дифференцируя это
выражение по переменным х и у, получим
∂∂x F (x , y , z (x, y)) = ∂∂Fx + ∂∂Fz ∂∂xz = 0 ,
∂∂y F (x , y , z (x, y )) = ∂∂Fy + ∂∂Fz ∂∂yz = 0 .
Отсюда (при условии |
∂F |
≠ 0 , используя |
обозначения |
∂F |
= F′ |
и |
∂F |
= F′) |
||||||||
|
|
|
|
|||||||||||||
|
∂z |
|
|
|
|
|
|
|
|
∂x |
x |
|
∂y |
y |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
получим окончательно |
|
F x′ |
|
|
|
|
Fz′ |
|
|
|
|
|
|
|||
|
|
|
∂ z |
= − |
и |
|
∂z |
= − |
|
|
|
|
|
(2.8) |
||
|
|
|
∂ x |
F z′ |
|
∂y |
Fz′ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Замечание 1. Уравнение F(x, y, z) =0 не всегда определяет одну переменную как
неявную функцию двух других. |
Так, уравнение x2 + y2 + z2 − 4 = 0 определяет |
||||||
|
|
|
|
|
|
||
функции |
z1 = 4 − x2 − y 2 и |
z2 = − 4 − x 2 |
− y 2 , определенные в круге |
||||
x2 + y2 ≤ 4 , |
а уравнение cos(x + 2y + 3z) − 4 = 0 |
не определяет вообще никакой |
|||||
функции.
Имеет место следующее утверждение, которое мы приведем без доказательства.
125
Теорема 2.4. (о существовании неявной функции). Если функция F(x, y, z) =0 и
|
′ |
′ |
′ |
|
ее производные Fx |
(x , y , z), Fy (x , y , z), Fz (x , y , z) определены и непрерывны в |
|||
некоторой |
окрестности |
точки M 0 (x0 ; y0 ; z0 ) , причем F(x0 , y0 , z0 ) = 0, а |
||
′ |
|
то существует |
окрестность точки M0 , в которой |
|
Fz (x0 , y0 , z0 ) ≠ 0 , |
||||
уравнение |
F(x, y, z) =0 |
определяет |
единственную функцию z = f (x, y) , |
|
непрерывную и дифференцируемую в окрестности точки (x0 ; y0 ) и такую, что f (x0 , y0 ) = z0 .
Замечание 2. Уравнение F(x, y) =0 задаёт неявную функцию одной
переменной. Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y ′x = − |
|
Fx′ |
|
(Fy′ ≠ 0). |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fy′ |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
2.9. |
|
Найти |
|
частные производные |
функции |
z, |
заданной |
неявно |
уравнением |
||||||||||||||||||||||||||||
e z + z − x 2 y + 1 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. |
Здесь F(x, y, z) =e |
z |
+ z −x |
2 |
y |
+1, |
|
|
′ |
|
′ |
=−x |
2 |
, |
′ |
z |
+1. По |
формулам |
||||||||||||||||||||
|
|
|
|
|
Fx |
= −2xy, Fy |
|
Fz =e |
|
|||||||||||||||||||||||||||||
(2.8) вычислим |
|
∂z |
= |
2xy |
|
, |
|
|
∂z |
= |
|
|
|
x2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∂x |
e |
z |
|
|
|
|
|
|
∂y |
|
e |
z |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример |
2.10. |
|
Найти |
|
|
dy |
|
, |
если |
|
|
неявная |
|
функция |
|
y = f (x) |
задана |
уравнением |
||||||||||||||||||||
|
|
|
dx |
|
|
|
|
|
||||||||||||||||||||||||||||||
y3 + 2 y = 2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. |
|
|
|
Здесь |
|
|
|
|
F(x; y) = y3 + 2y −2x, |
Fx′ = −2, |
Fy′ = 3y2 +2 . |
Следовательно, |
||||||||||||||||||||||||||
y′x = − |
|
− 2 |
|
, т.е. |
dy |
|
= |
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3y 2 + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
3y 2 + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
§2.4. Частные производные и дифференциалы высших порядков |
|||||||||||||||||||||||||||||||||||||
Пусть частные производные |
∂z |
, ∂z |
функции z = f (x, y), |
определенной в |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
||
области D , существуют в каждой точке этой области.
В этом случае частные производные представляют собой функции двух переменных x и y, также определенных в области D . Эти функции могут, в свою очередь, иметь частные производные, называемые вторыми частными
производными |
или |
частными производными второго порядка функции |
||||||
z = f (x, y). Они определяются и обозначаются следующим образом: |
||||||||
|
∂ |
∂z |
= |
∂ 2 z |
= z′′ - вторая частная производная по переменной х; |
|||
|
|
|
|
|
|
|
||
|
∂x |
∂x |
∂x |
|
||||
|
|
2 |
xx |
|||||
|
|
|
|
|
|
|
||
126

|
∂ ∂z |
|
∂ 2 z |
′′ |
- вторая частная производная по переменной y; |
|||||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
∂y |
= z yy |
|||||||||||||||||||||
|
∂y |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
∂ ∂z |
= |
∂2 z |
= z′′ |
|
и |
|
∂ |
|
|
∂z |
= |
|
∂ 2 z |
= z′′ |
- |
смешанные |
частные |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
∂y∂x |
xy |
|
|
|
|
|
|
|
∂x∂y |
|
yx |
|
|
|
||||||||
|
∂x |
∂y |
|
|
|
|
|
|
∂y |
∂x |
|
|
|
|
|
|
||||||||||||
производные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Аналогично определяются |
|
частные |
производные |
и более |
высокого |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
′′′ |
|
∂ |
|
∂ ∂z |
|
|
∂3 z |
|
|
|
|
|
|||||
порядка, |
|
например, |
|
|
|
|
|
|
= |
|
|
|
|
- |
третья смешанная частная |
|||||||||||||
|
zxyx = |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
∂y ∂x |
|
|
∂x∂y∂x |
|
|
|
||||||||
производная.
Замечание. Запись, например, « ∂2 z » не означает возведение в квадрат. Читать
∂x2
её следует так «д два зет по д икс дважды».
Пример 2.11. Найти все вторые частные производные функции z = x3 y2 − x2 y4 . Решение. Сначала найдем первые частные производные:
∂∂xz = 3x2 y2 − 2xy4 , ∂∂yz = 2x3 y − 4x2 y3 .
Теперь дифференцируя каждую из полученных частных производных еще раз по каждой переменной, получим уже четыре частных производных второго порядка:
∂2 z |
= 6 xy2 − 2 y 4 , |
∂2 z |
= 6x2 y −8xy3 , |
∂2 z |
= 6x2 y −8xy3 , |
∂2 z |
= 2x3 −12x2 y2 . |
|
∂x2 |
∂xdy |
∂ydx |
∂y2 |
|||||
|
|
|
|
Заметим, что в последнем примере смешанные частные производные оказались равными. Это не случайно. Вообще, имеет место утверждение:
Теорема 2.5 (Шварца). Если частные производные высшего порядка непрерывны, то смешанные частные производные, отличающиеся только порядком дифференцирования, равны между собой.
В частности, непрерывные смешанные частные производные второго порядка равны между собой
|
∂2 z |
= |
∂2 z |
. |
|
∂x∂y |
∂y∂x |
||
|
|
|
||
Рассмотрим функцию z = f (x, y), |
которая неограниченное число раз |
|||
дифференцируема в каждой точке M области D .
Тогда дифференциал первого порядка этой функции равен dz = ∂∂xz dx + ∂∂yz dy .
Для сокращения записи второго и последующих дифференциалов введем символ d при помощи сокращения d = ∂∂x dx + ∂∂y dy и определим операцию
127
возведения этого символа в степень n как операцию возведения двучлена
∂ |
dx + |
∂ |
dy в степень n: |
|
|
|
|
|
|
|
|
|
|
|
|
||
∂x |
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
∂ |
|
∂ |
2 |
∂2 |
|
∂2 |
∂2 |
||||||
|
|
|
d 2 = |
|
dx + |
|
dy |
= |
|
|
dx2 |
+ 2 |
|
dxdy + |
|
|
dy2 |
|
|
|
∂x |
∂y |
∂x |
2 |
|
∂y |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
∂x∂y |
|
|
|||||
Тогда мы можем применить символ d для вычисления дифференциалов любого порядка
|
|
|
|
|
|
∂ |
|
|
|
∂ |
|
|
|
|
|
∂z |
|
|
∂z |
|
|
|
|
|
||||
|
|
dz = |
|
|
|
dx + |
|
|
|
dy z |
= |
|
|
|
dx + |
|
dy |
|
|
|
|
|||||||
|
|
∂x |
|
∂y |
∂x |
∂y |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
∂ |
|
|
∂ |
|
2 |
|
|
∂2 |
|
|
|
|
∂2 |
|
|
|
∂2 |
|
|
||||||||
d 2 z = |
|
dx + |
|
|
dy |
z = |
|
|
|
|
|
dx2 |
+ 2 |
|
|
dxdy + |
|
|
dy2 |
z = |
||||||||
∂x |
|
∂y |
∂x |
2 |
∂x∂y |
∂y |
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
= |
∂2 z dx2 + 2 |
|
∂2 z |
|
dxdy + |
∂2 z dy2 . |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
∂x2 |
|
|
|
|
∂x∂y |
|
|
∂y2 |
|
|
|
|
|
|
|
||||||||||
И, наконец, выражение для дифференциала порядка n можно записать в форме:
|
∂ |
|
∂ |
n |
||
d n z = |
|
dx + |
|
dy |
z . |
|
∂x |
∂y |
|||||
|
|
|
|
|||
§2.5. Формула Тейлора для функции двух переменных
Пусть функция z = f (x, y) задана в окрестности точки M0 (x0 ; y0 ) и n +1
раз дифференцируема в этой окрестности. По аналогии с тем, как было сделано с функцией одной переменной, можно представить функцию двух переменных
в виде многочлена n-го порядка по степеням |
x − x0 |
|
и y − y0 и некоторого |
||||||||||||||||||||||||
остаточного члена. Для случая n = 2 такое представление имеет вид |
|
|
|
||||||||||||||||||||||||
f (x, y ) = f (x0 , y0 ) + fx′(x0 , y0 ) (x − x0 ) + f y′(x0 , y0 ) ( y − y0 ) + |
|
|
|
|
|
||||||||||||||||||||||
+ |
1 |
( |
fxx |
(x0 , y0 ) (x − x0 ) |
2 |
+ 2 fxy |
(x0 , y0 ) |
(x − x0 )(y − y0 )+ f yy (x0 , y0 ) (y − y0 ) |
2 |
)+ R2 , |
|
||||||||||||||||
|
2! |
|
′′ |
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
|
|
|
′′ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где R2 |
|
- остаточный член, структура которого |
|
аналогична структуре |
|||||||||||||||||||||||
остаточного члена в формуле Тейлора для функции одной переменной. |
|
|
|||||||||||||||||||||||||
|
В общем случае, рассмотрим |
приращения ∆x = x − x0 |
и ∆y = y − y0 |
и |
|||||||||||||||||||||||
заметим, |
что при x → x0 и |
y → y0 |
они превращаются в дифференциалы и |
||||||||||||||||||||||||
входят в выражения для d n z |
|
|
. Тогда можно представить полное приращение |
||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∆z = f (M ) − f (M0 ) функции в точке M0 (x0 ; y0 ) |
для любой точки M (x; y ) |
из |
|||||||||||||||||||||||||
указанной окрестности формулой Тейлора |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
∆z = dz |
|
|
|
+ |
1 |
d 2 z |
+ … + |
1 |
d n z |
+ |
|
1 |
|
d n+1z |
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(n +1)! |
|
|
|
||||||||||||||
|
|
|
|
|
|
M 0 |
2! |
|
|
|
M 0 |
|
n! |
|
M0 |
|
|
N |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где N – некоторая точка указанной окрестности, зависящая от M (x; y ) .
128

Для закрепления материала решите самостоятельно следующие примеры и задачи.
Найти частные производные функций
2.1.а) z = ln (x + 
 x2 − y2 ); б) z = arctg xy ; в) z = ln (x2 + y2 ); г) u = z y x .
x2 − y2 ); б) z = arctg xy ; в) z = ln (x2 + y2 ); г) u = z y x .
2.2.а) z = (1 + xy)y ; б) u = x3 + yz2 + 3yx − x + z ; в) u = (sin x)yz .
Найти полный дифференциал
2.3.а) z = x2 y4 − x3 y3 + x4 y2 ; б) z = xx +− yy ; в) z = arctg 1x−+xyy .
Найти указанные производные
2.4. u = ex−2 y ; x = sin t; y = t3 ; dudt = ?
2.5. z = arcsin (x − y ); x = 3t; y = 4t3 ; dudt = ?
2.6.z = x2 ln y; x = uv ; y = 3u − 2v ; ∂∂uz = ? ∂∂vz = ?
Найти все частные производные второго порядка
2.7.а) z = ln tg(x + y) ; б) z = xsin (xy) + y cos(xy) .
2.8. z = ex (x cos y − y sin y ). Показать, что |
∂2 z |
+ |
∂2 z |
= 0 . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
∂x2 |
∂y2 |
|
|
|
|
|
|
|
|
|||
Для заданной функции f (x, y, z) = 0 |
найти |
∂z |
и ∂z |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
||
2.9. а) |
z |
3 |
y |
2 |
+ sin (xy ) = 0 ; б) |
e |
xz |
+ x |
3 |
cos y = 0 ; в) |
|
x |
2 |
|
2 y |
|
|||||
|
|
|
|
arctg |
|
|
+ x |
e |
|
= 0 ; |
|||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
г) ln(x2 + yz) + x3 z 2 = 0 ; д) z3 − 6 xz + y3 − 3 = 0 .
129
Глава 3. Исследование функций двух переменных
§3.1. Скалярное поле и его геометрия
Если в каждой точке пространства или части пространства определено значение некоторой величины, то говорят, что задано поле данной величины.
Поле называется скалярным полем, если рассматриваемая величина скалярная, т.е. вполне характеризуется своим числовым значением.
Пример скалярных полей дает поле температур, поле давления, поле высот над уровнем моря, поле электрического потенциала.
Задание скалярного поля осуществляется заданием скалярной функции точки М u = u(M ). Если в пространстве введена декартова система координат
Oxyz, то u = u(x, y, z).
Будем полагать, что эта функция имеет непрерывные частные производные по всем переменным.
Уравнение u(x, y, z) = C где C - постоянная, определяет некоторую
поверхность, на которой величина u сохраняет постоянное значение. Такая поверхность называется поверхностью уровня скалярного поля.
Например, если |
скалярное поля задано функцией |
u = x2 + y2 + z2 , |
то |
поверхности уровня |
имеют уравнения x2 + y2 + z2 = C . |
При C ≥ 0 |
они |
представляют собой семейство концентрических сфер с центром в начале координат и радиусами 
 С . Поверхности уровня для различных значений C не пересекаются. Таковой является геометрия скалярного поля потенциала, порожденного точечным электрическим зарядом.
С . Поверхности уровня для различных значений C не пересекаются. Таковой является геометрия скалярного поля потенциала, порожденного точечным электрическим зарядом.
Другой пример - поле температур, возникающее вокруг равномерно нагретой прямой нити. Поверхности уровня такого поля - круговые цилиндры, общей осью которых служит эта нить.
Скалярное поле называется плоским, если существует плоскость такая, что во всех плоскостях, параллельных этой, скалярное поле будет одним и тем же. Если эту плоскость принять за плоскость Oхy, то скалярное поле определится скалярной функцией u = u(x, y) , т.е. не будет зависеть от z. В этом случае
уравнения u(x, y) = C представляют собой уравнения линий уровня поля.
Другими словами, линии уровня поля – это линии на плоскости Oxy, на которых функция u(x, y) постоянна.
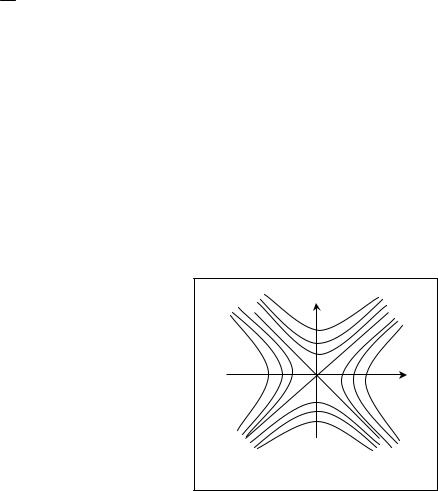
Пример 3.1. Найти линии уровня скалярного поля
u = x2 − y2 .
Решение. Линии уровня поля определяются
уравнениями x2 − y2 = c . При с = 0 получаем пару прямых y = x, y = −x .
При c ≠ 0 получаем семейство гипербол (рис.3.1).
Рис. 3.1
130
