ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник
.pdf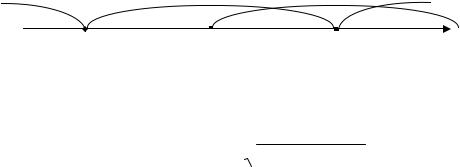
образом, производная |
′ |
меняет |
|
знак |
с |
“минуса” на “плюс” |
|
и, |
||||
f (x) |
|
|
||||||||||
следовательно, функция |
f (x) , согласно п.1.8.1, имеет в точке x0 минимум. |
|
|
|||||||||
Совершенно аналогично можно показать, |
что если f ′′( x0 ) < 0 , то f ′(x) |
в |
||||||||||
точке x0 меняет знак плюс на минус, т.е. в точке x0 |
функция имеет максимум. |
|
|
|||||||||
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
Приведем некоторые примеры исследований функций на экстремум. |
|
|
|
|||||||||
Пример 3.1. Найти экстремум функции |
f (x) = 2x3 −15x2 + 36x −14 . |
x |
|
2 |
||||||||
Решение. Так как f ′(x) = 6x2 −30x + |
36 = 6 |
( |
x −2 |
)( |
|
) |
, то стационарные точки |
= |
||||
|
|
x −3 |
|
|
||||||||
и x = 3 . Экстремумы функции могут быть только в этих точках. При переходе через x = 2 производная меняет знак “+” на “−”, следовательно, в этой точке функция имеет максимум.
При переходе через точку x = 3 производная меняет знак “−” на “+”, следовательно, в этой точке функция имеет минимум. Вычислив значения функции в точках x = 2 и x = 3 ,
найдем экстремумы функции: максимум |
f (2) =14 и минимум f (3) =13 . |
|||
Тот же результат |
можно |
получить, используя |
вторую производную. Так как |
|
′′ |
(2) = −6 |
< 0, |
а f ′′(3) = 6 > 0 , |
то в точке x= 2 функция имеет |
f ( x) = 12 x − 30 , то f″ |
||||
максимум, а при x=3 - минимум. |
|
(x + 3)3 |
|
|
|
|
|
|
|
Пример 3.2. Найти экстремумы функции |
f (x)= (x +1)2 . |
|
||
Решение. Найдем производную этой функции:
f ′(x) = |
(x + 1)2 3(x + 3)2 − (x + 3)3 2(x + 1) |
= |
(x + 3)2 (x − 3). |
|
(x + 1)4 |
|
(x + 1)3 |
Стационарные точки функции x=−3 и x=3. Точка x=−1 является критической, но не является стационарной, потому что при x=−1 функция не определена.
Легко видеть, что при переходе через точку x=−3 производная не меняет знака, следовательно, точка x=−3 не является точкой экстремума.
В точке x=3 производная меняет знак с “−” на “+”, следовательно, в этой точке
минимум. Находим |
f (3) = |
63 |
= 13,5 . |
|
|
|
|
|
|
|
|
|
|
||||
|
|
42 |
|
|
|
|
|
|
Замечание. Для |
определения знака |
производной |
достаточно решить неравенство |
|||||
(x + 3)2 (x − 3) ≥ 0 . Это неравенство решается методом интервалов (рис.3.4). |
|
|
||||||
(x + 1)3 |
|
|
|
|
|
|
|
|
|
+ |
+ |
− |
+ |
x |
|
||
|
|
−3 |
−1 |
3 |
|
|||
|
|
|
|
|||||
|
|
|
|
|
Рис. 3.4 |
|
|
|
Отсюда видно, что при переходе через точку x=−3 производная не меняет знака, а при |
||||||||
переходе через точку x=3 знак производной меняется с “−” на “+”. Точка x=−1 не является точкой максимума, потому что в этой точке функция не определена.
Пример 3.3. Найти экстремум функции f (x ) = 3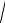 
(1 − x )(x − 2 )2 . Решение. Находим производную функции:
101
|
|
|
f ′(x ) = (1 − x ) 2 (x − 2 )− (x − |
2 )2 |
= |
|
4 − 3 x |
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
3 3 (1 − x )2 (x − 2 )4 |
|
3 3 |
(1 − x )2 (x − 2 ) |
|||||
|
x = |
3 |
|
|
|
|
|
|
|
|
|
|
При |
|
4 |
производная |
равна |
нулю, |
а при x=1 и |
x=2 производная не существует, |
|||||
|
|
|||||||||||
следовательно, точки x = 1 , |
x = |
4 |
, x = 2 |
критические точки функции. При переходе через |
||||||||
|
||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
точку x=1 производная не меняет знака и, следовательно, эта точка не является точкой экстремума.
При переходе через точку x = 43 производная меняет знак минус на плюс,
следовательно, в точке x = 43 функция имеет минимум. При переходе через точку x=2
производная меняет знак с “+” на ”−“, т. е. точка x=2 - точка максимума. Минимум функции
равен |
|
4 |
|
|
3 |
4 |
, а максимум равен f (2) |
= 0. |
f |
|
|
= − |
|
|
|||
|
|
3 |
|
|
2 |
|
|
|
Наибольшее и наименьшее значение функции
Согласно теореме Вейерштрасса, всякая непрерывная на отрезке функция достигает на этом отрезке своего наибольшего и наименьшего значений. Алгоритм нахождения наибольшего и наименьшего значений функции состоит в следующем.
Пусть f (x) |
непрерывна на отрезке [a,b] и имеет на нем к стационарных |
точек x1,...,xk . |
Тогда наибольшее значение функции f (x) на отрезке [a,b] |
равно наибольшему из чисел f (a), f (x1),…f (xk), f (b), а наименьшее значение функции f (x) - наименьшему из этих чисел.
Пример 3.4. Найти наибольшее и наименьшее значения функции
f (x) = 2x3− 3x2− 36x− 8 на отрезке [−3, 6].
Решение. Находим производную функции: f′(x) = 6 (x+2) (x−3) . Таким образом, стационарные точки функции: x = −2 и x = 3. Вычисляем значения функции f (−3), f (−2), f (3), f (6) . Эти значения соответственно равны: f (−3) = 100, f (−2) = 36, f (3) = −89, f (6) = 100.
Отсюда, наибольшее значение функции f (6) = 100, наименьшее – f (3) = −89.
§3.4. Выпуклость и вогнутость графика функции
Рассмотрим на плоскости график некоторой однозначной дифференцируемой функции y = f ( x) . Важной характеристикой формы этого
графика является не только возрастание и убывание, но и направление выпуклости и вогнутости кривой. Определим эти понятия.
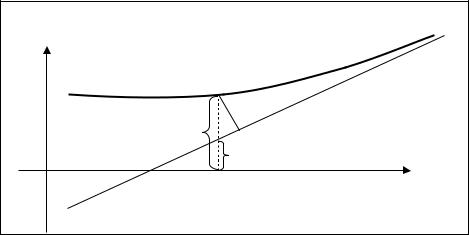
Определение 3.7. График дифференцируемой функции y = f ( x) называется вогнутым на интервале (a,b), если при любых x (a,b) кривая y = f ( x)
расположена выше касательной, проведенной к кривой в точке M (x, f (x)) (рис. 3.5).
102
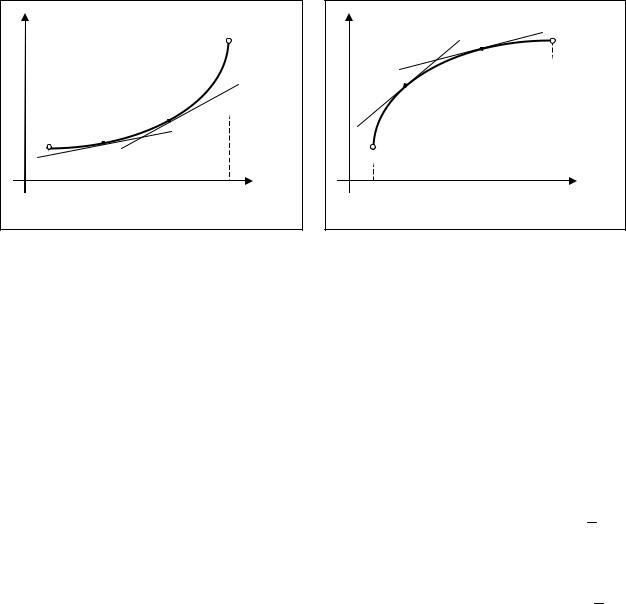
Определение 3.8. График дифференцируемой функции y = f ( x) называется выпуклым на интервале (a,b), если при любых x (a,b) кривая y = f ( x)
расположена ниже касательной, проведенной к кривой в точке M (x, f (x)) (рис. 3.6).
y |
y |
a |
b |
x |
a |
b |
x |
|
|
||||
|
Рис.3.5 |
|
|
Рис.3.6 |
|
Для нахождения промежутков выпуклости и вогнутости графика функции можно использовать следующее утверждение.
Теорема 3.7. Если для дважды дифференцируемой функции y = f ( x) вторая ее производная f ′′( x) положительна в каждой точке промежутка (a,b), то
график этой функции вогнутый ( ) на данном промежутке.
Если же вторая производная f ′′( x) отрицательна, в каждой точке промежутка (a,b), то график функции f (x) выпуклый (∩) на данном
промежутке.
Доказательство. Докажем первую часть теоремы. Пусть f ′′( x) > 0 , при любом x из интервала (a,b), и пусть x0 произвольная точка из этого интервала. Через
точку M0 (x0, f (x0)) графика функции |
f (x) проведем касательную |
y |
. Как |
|||
известно, уравнение этой касательной задается уравнением |
|
|
|
|
||
|
|
′ |
(3.5) |
|||
y = f (x0 )+ f (x0 )(x − x0 ). |
||||||
Сравним в точке x (a,b) |
ординаты кривой y = f ( x) и касательной |
y |
, для |
|||
этого рассмотрим разность δ = y − y . Используя (3.5), имеем: |
|
|
|
|
||
δ = y − y = f (x)− f (x0 )− f ′(x0 )(x − x0 ) |
(3.6) |
|||||
По теореме Лагранжа справедливо равенство: |
|
|
|
|
||
|
|
′ |
|
|
|
|
f (x) − f (x0 ) = f (c)(x − x0 ), |
|
|
|
|
||
где с лежит между x и x0 и поэтому из (3.6) получаем: |
|
|
|
|
||
δ = (x − x0 ) [ f ′(c) − f ′(x0 )] . |
(3.7) |
|||||
Используя еще раз теорему Лагранжа, имеем: |
|
|
|
|
||
′ |
′ |
′′ |
|
|
|
|
f (c) − f (x0 ) = f (c1)(c − x0 ) , |
|
|
|
|
||
103
где с1 лежит между с и x0 , поэтому из (3.7) имеем:
δ = (x − x0 )(c − x0 ) f ′′(c1) .
По условию теоремы f″ (c1)> 0. Если x > x0 , то также c > x0 и, следовательно, (x−x0) (c−x0) > 0, т. е., и в этом случае δ > 0. Таким образом, при
x ≠ x0 |
всегда имеем δ = y − y > 0 , т.е. |
y > y0 . |
|
Отсюда следует, что при любом |
x из интервала (a,b) |
график функции |
|
f (x) |
расположен выше своих касательных, т. е., график |
функции f (x) |
|
является выпуклым на этом интервале.
Вторая часть теоремы доказывается совершенно аналогично. Теорема доказана.
Точки перегиба
Определение 3.9. Точка M0 (x0 , f (x0 )) называется точкой перегиба кривой y = f ( x) , если можно найти такое число δ > 0 , что на отрезке [x0 − δ; x0 ] она выпукла, а на отрезке [x0 ; x0 + δ] она вогнута; или наоборот.
Таким образом, точка перегиба всегда отделяет выпуклую часть кривой от вогнутой части, а касательная к кривой (если она существует) в точке перегиба пересекает эту кривую. В дальнейшем точку перегиба часто будем обозначать только её абсциссой.
Для нахождения точек перегиба можно воспользоваться следующим утверждением.
Теорема 3.9. Если для функции f (x) ее вторая производная f ′′( x) в точке x0
обращается в нуль (или не существует) и при переходе через эту точку меняет свой знак на противоположный, то точка графика M0 (x0, f (x0)) является точкой перегиба.
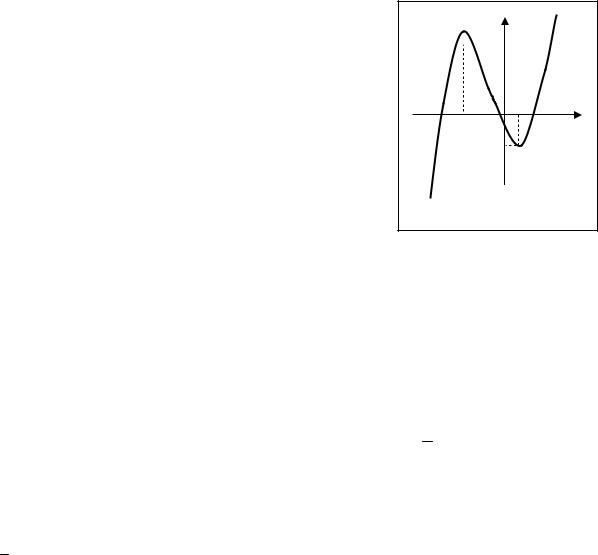
Доказательство. Предположим, что вторая производная f ′′( x) в точке x0
обращается в нуль и меняет свой знак с плюса на минус. Тогда левее точки x0 вторая производная положительна и, следовательно, по теореме 3.7, график функции - вогнутая кривая. Правее точки x0 вторая производная отрицательна и, следовательно, график функции выпуклый (рис.3.7).
y
М0
x
x0
Рис. 3.7
104
Таким образом, в точке M0 кривая меняет вогнутость на выпуклость и, следовательно, точка М0 - точка перегиба графика этой функции. Теорема доказана.
§3.5. Асимптоты графика функции и их нахождение
Рассматривая график функции на интервале (a,b), мы вынуждены
удовлетворяться лишь его частью, поскольку этот интервал всегда конечен. Однако большой интерес вызывает поведение функции «на бесконечности», т.е. при неограниченном возрастании (по абсолютной величине) абсциссы и/или ординаты переменной точки кривой. Важным частным случаем при этом является неограниченное приближение графика функции к некоторой прямой. Рассмотрим этот случай подробнее.
Определение 3.10. Прямая линия называется асимптотой кривой, если расстояние δ от точки кривой до этой прямой по мере удаления точки в том или ином направлении в бесконечность стремится к нулю.
|
Вертикальные асимптоты |
Если lim |
f (x) = ∞ или lim f (x) = ∞, то прямая x = x0 - называется |
x→x0 −0 |
x→x0 +0 |
вертикальной асимптотой графика функции y = f ( x) . Например, прямая x = 0
|
|
|
|
|
|
|
|
|
y = x |
|
y |
|
ln x |
|
является вертикальной асимптотой графиков функций |
1 |
и |
|
= |
|
, так как |
||||||||
|
|
|
||||||||||||
lim |
1 |
= ∞, |
lim |
1 |
= −∞ и |
lim ln x = −∞ . График функции tg |
x имеет |
|||||||
|
|
|||||||||||||
x→0+0 x |
x→0−0 |
x |
x→0+0 |
|
|
|
|
|
|
|
||||
бесконечно |
много вертикальных |
асимптот: |
каждая |
|
из |
прямых |
||||||||
π |
|
|
|
|
является асимптотой. |
|
|
|
|
|
|
|||
x = 2 + kπ , |
k = 0, ± 1, ± 2, ... |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
Отсюда вытекает правило нахождения вертикальных асимптот. |
||||||||||||||
Первоначально находятся точки x1, x2, |
… xk , в которых функция |
f (x) не |
||||||||||||
определена, а затем вычисляются всевозможные односторонние пределы
функции f (x) в этих точках, а именно, вычисляются пределы lim f (x) и
x→xi+0
lim f (x), i =1,2,...,k . Если, по крайней мере, один из этих пределов равен
x→xi−0
+∞ или −∞, то прямая x = xi является вертикальной асимптотой.
Горизонтальные и наклонные асимптоты
Предположим, что график функции f (x) имеет наклонную асимптоту Y = kx + b в направлении положительной оси x , как это изображено на рис. 3.8.
105
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
6 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
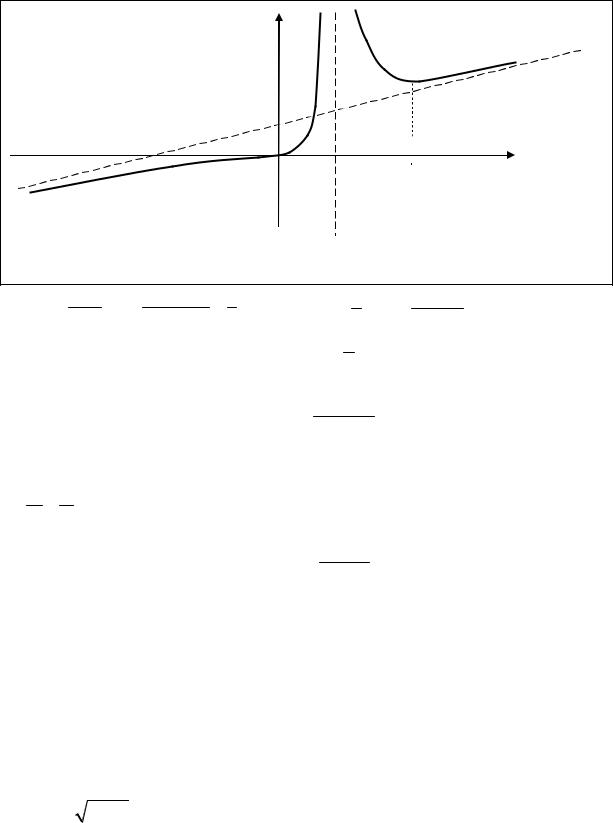
Рис. 3.10 |
|
|
|
|
|
|
|
k = lim |
f ( x) |
= lim |
x3 |
= |
1 |
. |
|
|
1 |
|
|
x ( x − 1) |
= 1 . |
|||
x |
|
− x) 2 |
4 |
b = lim f ( x ) − |
4 |
= lim |
( x |
− 2) 2 |
||||||||
x→∞ |
x→∞ 4 x(2 |
|
|
x → ∞ |
|
|
x →∞ |
|
||||||||
Итак, график имеет наклонную асимптоту |
y = 1 x + 1 . |
|
|
|
||||||||||||
Вычислим первую производную: |
|
4 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
′ |
x2 (x − 6) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
f (x) = |
4(x − 2)2 . |
|
|
|
|
||
Очевидно, точка x = 6 |
- экстремум функции. |
На интервалах |
(−∞,2) (6,+∞) функция |
|||||||||||||
возрастает, |
на интервале |
(2,6) убывает. Следовательно, |
точка |
x = 6 - точка минимума и |
||||||||||||
f (6) = 26 = |
13 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим вторую производную |
|
|
6x |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
f ′′(x) = |
(x − 2)4 . |
|
|
|
|
||
Мы видим, что функция имеет единственную точку перегиба при x= 0. Если x< 0 ,то |
||||||||||||||||
функция выпукла вверх, поэтому ее график при x→ −∞ приближается к асимптоте снизу. |
||||||||||||||||
При 0 < x < 2 и при x > 2 |
функция выпукла вниз. Отсюда следует, что при x→ +∞ график |
|||||||||||||||
приближается к асимптоте сверху. Вычислив еще несколько точек графика, на основе |
||||||||||||||||
проведенных исследований делаем эскиз графика функции. |
|
|
|
|||||||||||||
Для закрепления материала решите самостоятельно следующие примеры и задачи.
Исследовать функции на монотонность: найти участки возрастания и убывания, найти точки экстремумов.
3.1. |
|
|
|
3.2. |
y = |
1 |
x |
3 |
+ |
1 |
x |
2 |
− 2 x − 1 |
3.3. |
y = |
ex |
|
|||
y = ln 1 + x2 |
||||||||||||||||||||
3 |
|
2 |
|
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|||||
3.4. |
y = x + cos x |
3.5. |
y = ln (1+ x)− x + |
|
3.6. |
y = x3e−x |
||||||||||||||
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
Найти точки перегиба, участки выпуклости и вогнутости графиков функций
109
