
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник
.pdf
y′x |
= lim |
∆y |
(1.11) |
|
∆x→0 |
∆x |
|
∆y
Отношение ∆x можно преобразовать следующим образом:
∆y = ∆y ∆u
∆x ∆u ∆x .
Подставляя полученное выражение в (1.11) и используя свойства пределов, имеем:
|
|
y′x |
= lim |
∆y |
= lim |
∆y |
∆u |
= lim |
∆y |
lim |
∆u |
(1.12) |
||
|
∆u |
|
∆x→0 |
∆x |
∆x→0 |
∆u |
∆x |
∆x→0 |
∆u |
∆x→0 |
∆x |
|
||
Так как lim |
= u′x , то нам остается доказать, что |
|
|
|
|
|||||||||
∆x→0 |
∆x |
|
|
|
|
|
∆y |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
= yu′ |
|
|
|
(1.13) |
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
∆x→0 |
∆u |
|
|
|
|
|
|||
Для установления справедливости равенства (1.13), необходимо доказать что ∆u → 0 при ∆x → 0 . Но функция u = u(x) имеет производную и, следовательно,
она непрерывна, а это в свою очередь означает, что при ∆x , стремящемся к нулю, ∆u также стремится к нулю. И тогда
lim ∆y = lim |
∆y = y′ . |
||
∆x→0 ∆u |
∆u→0 ∆u |
u |
|
|
|||
Из доказанных равенств следует справедливость утверждения 1.11. Следствие. Правило дифференцирования сложной функции остаётся в силе,
если |
промежуточных аргументов |
несколько. |
Так, |
если y = f (u) , |
u = u(v) , |
|||||||||||||||||||||||||||||||||||||
v = g(x) , |
то |
y′ |
= y′ |
u′ |
v′ . Действительно, |
в |
этом |
случае по |
доказанному |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
u |
|
v |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
утверждению u′ |
= u′ |
v′ |
, и следствие становится очевидным. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Пример 1.1. |
|
|
x |
v |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(sin( x2 + 4))′ = u = x2 + 4 = (sin u )′ = cos u u′ = cos u 2x = 2x cos (x2 + 4). |
||||||||||||||||||||||||||||||||||||||||||
Пример 1.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
′ |
1 |
|
|
|
|
|
|
′ |
|
|
|
|
|
1 |
|
|
|
|
′ |
|
|
|||||
|
|
|
|
tg x |
|
|
|
|
tg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
( |
|
|
|
+ 1 ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
e |
|
|
u = e |
|
+ 1 = ( |
|
|
u ) |
= |
|
|
|
|
|
|
u |
|
= |
|
v = tg x = |
|
|
|
e |
|
v |
|
= |
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
u |
|
e tg x + 1 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
1 |
|
|
|
|
|
e |
tg x |
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
co s 2 x |
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 1.3. |
|
|
|
|
|
|
|
2 e tg x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(ln 2 c o s x )′ = u = ln co s x = (u 2 )′ = 2u u ′ = 2 ln co s x (ln v )′ = v = c o s x = |
. |
|||||||||||||||||||||||||||||||||||||||||
|
|
2 ln c o s x |
|
|
|
|
|
2 ln c o s x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
|
(co s x )′ = − sin x |
= −2 tg x ln c o s x. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
co s x |
|
|
|
|
co s x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
71
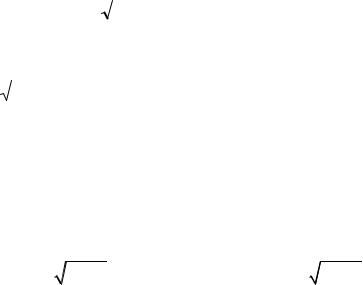
Производная обратной функции |
||
Пусть |
y = f (x) и x = ϕ( y) - |
взаимно обратные функции, т.е. такие, что |
y = f (ϕ( y )) |
и x = ϕ( f (x)). |
|
Предложение 1.12. Если функция |
y = f (x) строго монотонна на некотором |
|
|
|
′ |
интервале и имеет не равную нулю производную f (x) в некоторой точке х |
||
этого интервала, то обратная ей функция x = ϕ( y) также имеет производную |
||
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ ( y) в соответствующей точке y , причём эта производная определяется |
||||||||||||||||||||
равенством ϕ′( y) = |
|
1 |
или x′y |
= |
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|||
f ′(x) |
|
′ |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
yx |
|
|
|
|
|
|
|
|
||||||
Доказательство. Рассмотрим обратную функцию x = ϕ( y) . |
Дадим аргументу y |
|||||||||||||||||||
приращение ∆y ≠ 0 . |
Ему соответствует приращение ∆x |
|
обратной функции, |
|||||||||||||||||
причём ∆x ≠ 0 в |
силу |
строгой |
монотонности функции |
|
y = f (x) . Поэтому |
|||||||||||||||
можно записать |
|
|
|
|
|
|
|
|
|
|
∆x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
(1.14) |
||||
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
∆y |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||
Если ∆y → 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x |
|
|
|
||
то, в силу непрерывности обратной функции, приращение |
||||||||||||||||||||
∆x → 0 . И так как lim |
∆y |
= f ′(x) ≠ 0 , то из (1.14) следуют равенства |
||||||||||||||||||
|
∆x →0 |
∆x |
∆x = |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
lim |
|
|
= |
|
|
, т.е. ϕ′( y) = |
|
|
. |
|||||||||
|
|
|
|
∆y |
|
′ |
|
|
|
|||||||||||
|
|
∆y→0 |
∆y |
|
|
|
|
|
|
|
|
|
|
′ |
||||||
|
|
|
|
|
|
|
|
f (x) |
|
|
f (x) |
|||||||||
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
∆x |
→0 |
|
|
|
|
|
|
|
|
||||||
Таким образом, производная обратной функции равна обратной величине производной данной функции.
Пример 1.4. Пользуясь правилом дифференцирования обратной функции, найти
производную y′x |
для функции y = 3 |
|
|
|||||||||
x −1. |
||||||||||||
Решение. |
Обратная функция x = y 3 +1 имеет производную x′y = 3y2 . Следовательно, |
|||||||||||
1 |
|
1 |
|
1 |
|
|
|
|
||||
y ′x = |
|
= |
|
|
= |
|
|
|
|
. |
||
x ′y |
3 y 2 |
3 3 |
|
|
||||||||
|
( x −1) 2 |
|||||||||||
Производные обратных тригонометрических функций
В этом пункте будут установлены правила дифференцирования обратных
тригонометрических функций. |
|
|
|
|
|
|
|
|
|
|
|
y = arcsin x , |
|
|
y = arccos x , |
||||||||||
Предложение 1.13: Производные |
функций |
|
|
||||||||||||||||||||||
y = arctg x , y = arcctg x |
находятся по формулам |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(arcsin x)′ = |
1 |
|
, |
|
|
x |
|
<1 ; |
(arccos x)′ = − |
|
|
1 |
|
, |
|
|
x |
|
<1 ; |
||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
1− x2 |
|
|
|
( |
|
|
|
|
|
) |
|
1 |
− x2 |
|
|
( |
|
|
|
) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(arctg x)′ = |
|
|
|
|
1 |
|
|
|
(arcctg x)′ |
1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
, |
= − |
|
. |
|
|
|
|
|
|
|
||||||||||||
|
1+ x2 |
1+ x2 |
|
|
|
|
|
|
|
||||||||||||||||
72
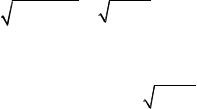
Доказательство. |
|
Доказательство |
|
проведем |
|
для двух |
|
функций |
arcsin x и |
|||||||||||||||||||||||||||||
arcctg x ; для двух оставшихся функций доказательства аналогичны. |
|
|||||||||||||||||||||||||||||||||||||
1. Если y = arcsin x , то x = sin y . Используя правило дифференцирования |
||||||||||||||||||||||||||||||||||||||
обратной функции, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
y′ = |
|
|
|
1 |
|
|
|
= |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
(sin y )′ |
|
cos y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Но cos y = |
|
|
|
|
|
|
|
|
|
Отсюда |
|
и из |
предыдущего |
равенства |
||||||||||||||||||||||||
1 − sin 2 y = |
1 − x2 . |
|
|
|||||||||||||||||||||||||||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ = (arcsin x)′ = |
|
|
|
|
1 |
|
|
|
, |
(имея в виду, что |
|
x |
|
<1). |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
− x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2. Если y = arcctg x , то x = ctg y . По формуле для производной обратной |
||||||||||||||||||||||||||||||||||||||
функции имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ = |
1 |
|
|
|
|
|
= |
|
|
|
|
1 |
|
|
|
|
|
|
= −sin2 |
y . |
|
|||||||||||||||
|
|
|
|
|
′ |
|
|
1 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
(ctg y) y |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
sin |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Используя тригонометрическое тождество 1+ ctg2 x = |
1 |
|
|
|
, получим |
|
||||||||||||||||||||||||||||||||
sin2 |
x |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
y |
′ |
|
|
|
2 |
y |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
= −sin |
|
= −1 + ctg |
2 y = −1 + x2 . |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Предложение доказано.
Сводка основных формул дифференцирования
Выведенные правила дифференцирования, формулы производных основных элементарных функций запишем в виде таблицы.
На практике чаще всего приходится находить производные от сложных функций. Поэтому в приведённой ниже таблице формул дифференцирования аргумент х заменён на промежуточный аргумент u.
Правила дифференцирования
1. |
(u ± v) |
′ |
= u |
′ |
′ |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
± v ; |
|
|
|
|
|
|
|
|
|
|||||||||||
2. |
(u v) |
′ |
|
|
′ |
|
|
|
′ |
|
в частности, |
(cu ) |
′ |
|
|
|
′ |
|||||
|
= u v + uv , |
|
= c u ; |
|||||||||||||||||||
|
u |
′ |
|
|
|
|
′ |
− uv |
′ |
|
|
c |
′ |
|
|
cu′ |
|
|||||
|
|
|
|
|
u v |
|
|
|
|
|
|
|
||||||||||
3. |
|
|
|
|
= |
|
|
|
|
|
, |
в частности |
|
= − |
|
2 |
; |
|||||
|
|
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
v |
|
|
|
u |
|
|
|
v |
|
|||||
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4. |
y′x = yu′ u ′x ; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5. |
y′x |
= |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x′y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
73

Формулы дифференцирования
1.(c)′ = 0 ;
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Пример 1.5.
(u a )′ = a u a−1 u′ , в частности, ( |
|
)′ = |
|
1 |
|
u′ |
; |
1 |
′ |
= − |
1 |
u′; |
|||||||||||||||||||||||||||||||
u |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
u |
|
|
|
|
u |
|
u2 |
|
||||||||
(a u )′ = a u ln a u ′, в частности, (eu )′ = eu u′ ; |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
(log a u)′ = |
1 |
|
|
|
|
|
|
u′ , в частности (ln u)′ = |
1 |
|
u′; |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
u ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(sin u)′ = cos u u ′ ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(cos u) |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= −sin u u ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
(tg u) |
′ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= cos 2 u u ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
(ctg u) |
′ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= − sin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
u u ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
(arcsin u)′ = |
|
|
|
|
1 |
|
|
|
|
|
u′ ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
− u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
1 |
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(arccos u) |
|
= − |
|
|
|
|
|
|
|
|
|
u ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
1− u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(arctg u) |
′ |
= |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1+ u 2 u ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
(arcctg u) |
′ |
|
|
|
|
|
|
1 |
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= −1 |
+ u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
u ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Найти производную функции |
y |
|
2x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
= tg x. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 x 3 ′ |
|
(x 3 )′ tg x − x 3 (tg x )′ |
|
3 x 2 tg x − x 3 |
1 |
|
|
|
|
|
||||||||
|
|
|
2 |
x |
|
|
|
|||||||||||||
Решение. |
y ′ = |
|
|
= 2 |
|
(tg x ) |
2 |
= 2 |
|
|
cos |
. |
|
|||||||
|
|
(tg x ) |
2 |
|
|
|
||||||||||||||
|
|
tg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 1.6. Найти производную функции y = cos (ln3 2x ). |
|
|
|
|
|
|
|
|||||||||||||
Решение. |
y′ = − sin (ln |
3 2 x ) 3ln |
2 2x |
1 |
2 . |
|
|
|
|
|
|
|
|
|
|
|
||||
2 x |
5 − x |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 1.7. Найти производную функции y = |
. |
|
|
|
|
|
|
|
|
|||||||||||
tg x +1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
|
y′ = (5 − x )′ (tg x + 1) − (5 − x ) (tg x + 1)′ = |
− (tg x + 1) − (5 − x ) |
|
|
||||||||||||||||
Решение. |
cos2 x |
|
||||||||||||||||||
(tg x + 1)2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
(tg x + 1)2 |
|
|
|
|
|
|
|
|
|
|
|||||
Пример 1.8. Найти производную функции y = arcsin 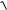
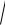 x +0,5 . Решение.
x +0,5 . Решение.
y′ = (arcsin |
|
)′ = |
1 |
|
|
( |
|
)′ = |
|
|
1 |
|
|
|
1 |
|
= |
|||
x + 0,5 |
x + 0,5 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 − |
|
2 |
|
|
1 |
− x − 0,5 2 x + 0,5 |
|
|
|||||||||
|
|
|
x + 0,5 |
|
|
|
|
|||||||||||||
74
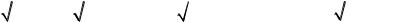
|
1 |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
. |
|||
= |
2 |
|
|
|
= 2 |
|
|
= |
|
|
|
|||||
0, 5 − x |
x + 0, 5 |
(0, 5 − x)( x + 0,5) |
1 − 4 x 2 |
|
|
|||||||||||
§1.5. Дифференциал
С понятием производной тесно связано понятие дифференциала. Этому понятию и будет посвящен настоящий параграф.
Определение дифференциала
Рассмотрим функцию y = f ( x) , которая имеет производную y′ = f ′(x) в
точке х и в некоторой окрестности этой точки. Значению х дадим приращение х. Обозначим у соответствующее приращение функции. Согласно
определению производной, мы можем записать
y ' = lim ∆y = f '(x) .
∆x→0 ∆x
На основании теоремы о связи предела и бесконечно малой величины мы можем записать, что в некоторой окрестности точки х справедливо равенство
|
|
∆y |
= f '(x) + α(∆x), |
(1.15) |
|
|
∆x |
||
|
|
|
|
|
где α(∆x) – бесконечно малая |
величина при ∆x → 0 . Умножая обе части |
|||
соотношения (1.15) на х, получим: |
|
|||
|
|
|
′ |
(1.16) |
|
|
∆y = f (x) ∆x + ∆x α(∆x) . |
||
Если |
′ |
|
|
|
f ( x) ≠ 0 , то первое слагаемое в (1.16) имеет тот же порядок малости, |
||||
что и х, |
а второе слагаемое ∆x α(∆x), при делении на |
x стремится к нулю |
||
при ∆x → 0 , |
т.е. имеет порядок малости более высокий, чем первое слагаемое. |
|||
Величина |
f |
′ |
(x) ∆x , уже вне зависимости от равенства нулю величины |
′ |
|
f (x) , |
|||
называется дифференциалом функции. Итак, мы пришли к следующему определению.
Определение 1.2. Дифференциалом функции y = f ( x) в точке х называется произведение производной y′ = f ′(x) , вычисляемой в заданной точке х, на
приращение аргумента ∆x .
Дифференциал обозначают dy или df ( x) , таким образом
dy = df ( x) = |
′ |
или dy = y |
′ |
∆x |
(1.17) |
f ( x) ∆x |
|
Как следует из определения, дифференциал зависит от двух переменных - точки дифференцирования х и приращения ∆x . Из (1.16) и (1.17) вытекает равенство
∆y = dy + dx α(∆x) , |
(1.18) |
т.е. дифференциал функции dy и её приращение ∆y отличается друг от друга на бесконечно малую величину ∆x α(∆x), более высокого порядка чем ∆x . Если
пренебречь бесконечно |
малой величиной ∆x α(∆x), то (1.18) даёт |
приближенное равенство |
∆y ≈ dy . Это равенство означает, что при достаточно |
малых ∆x приращение функции с большей степенью точности можно заменить
75
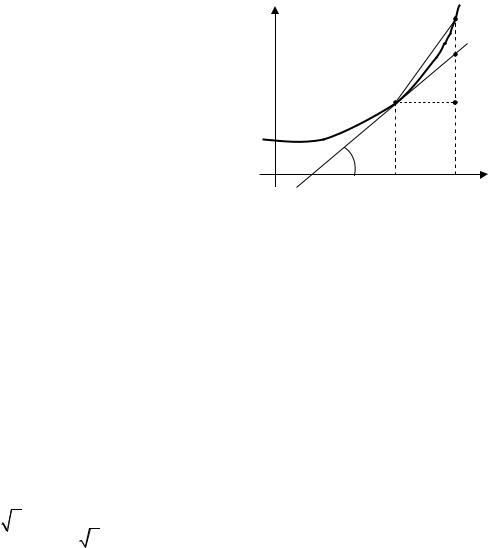
её дифференциалом. Заметим, что если |
y = x , то dy = y′ ∆x = ( x)′ ∆x = ∆x . С |
другой стороны dy = dx , и мы имеем весьма важное соотношение |
|
∆x = dx . |
(1.19) |
Учитывая это последнее равенство, соотношения (1.17), определяющее дифференциал, перепишем в виде
′ |
′ |
dx . |
(1.20) |
df (x) = f (x)dx или dy = y |
|||
Геометрический смысл дифференциала |
|
|
|
Рассмотрим функцию y = f ( x) , которая |
в точке х |
имеет производную |
|
y′ = f ′(x) . На рис.1.3 график функции выделен жирной линией. Прямая АС –
касательная к графику функции, проведенная |
|
|
|
||||||||||||||||||||||||
y |
|
|
|||||||||||||||||||||||||
в точке х и имеющая угол наклона к оси Ох, |
|
B |
|||||||||||||||||||||||||
равный α. Из приведенного рисунка видно, |
|
|
|
||||||||||||||||||||||||
что |
|
AD |
|
– приращение аргумента, |
|
BD |
|
= ∆y - |
|
|
C |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
приращение |
|
функции. |
Очевидно, |
|
A |
|
|||||||||||||||||||||
|
CD |
|
= |
|
AD |
|
|
tg |
α = |
′ ∆ |
dy |
= |
|
CD |
|
- |
|
D |
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
y x , т.е. |
|
|
|
|
|
|
|
||||||||||||
дифференциал функции. Следовательно, |
|
α |
|
||||||||||||||||||||||||
|
CB |
|
= ∆x α(∆x) . |
Отсюда |
вытекает, |
|
что |
|
x |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
геометрически дифференциал представляет |
|
x |
|||||||||||||||||||||||||
|
x+∆x |
||||||||||||||||||||||||||
собой приращение ординаты касательной к |
|
||||||||||||||||||||||||||
|
Рис.1.3 |
|
|||||||||||||||||||||||||
графику функции, проведенной в точке х. |
|
|
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
Таким образом, замена |
∆y на dy |
геометрически означает замену части |
|||||||||||||||||||
кривой графика функции частью касательной к этой кривой.
Из нашего рисунка видно, что дифференциал dy прямо пропорционален приращению аргумента x. Этот же вывод следует непосредственно из формулы dy = y′ ∆x , т.е. y′ – это коэффициент пропорциональности. Отсюда
можно сделать вывод: заменяя у на dy полагаем, что приближенно малые изменения функции пропорциональны соответствующим им малым изменениям аргумента, т.е. при малых изменениях всякая функция, имеющая производную, ведет себя как линейная.
Приведем ряд примеров нахождения дифференциалов.
Пример 1.9. y = x3 + 4x2 + 3, dy = (3x2 + 8x )dx .
Пример 1.10. y = |
|
, dy = |
dx |
|
|
. |
|
x |
|||||||
|
|
|
|||||
|
|
|
2 x |
||||
Пример 1.11. |
y = x5 , dy = 5x4dx . |
|||||
Пример 1.12. |
y = arctg2x , dy = |
|
2dx |
. |
||
|
1 |
+ 4 x2 |
||||
Пример 1.13. |
y = ln x , dy = |
dx |
. |
|
|
|
|
|
|
||||
|
|
x |
|
|
||
76
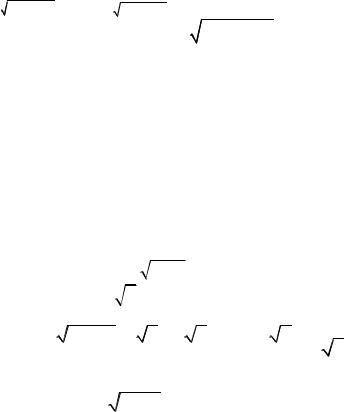
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
arcctgln x |
|
|
|
|
|
|
|
||||||||
Пример 1.14. y = e |
, dy = e |
arcctg ln x |
|
|
|
|
|
dx . |
||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||
|
|
|
|
|
1 + ln |
2 |
|
x |
||||||||
|
|
arcctg ln x |
||||||||||||||
|
|
|
|
2 |
|
|
|
|
x |
|
|
|||||
Применение дифференциалов в приближенных вычислениях
Применение дифференциалов в приближенных вычислениях основано на приближенном равенстве
∆y ≈ dy .
Но в этом соотношении |
∆y = f (x + ∆x) − f (x) , dy = f ′(x) ∆x . |
Отсюда |
||
получаем формулу приближенного |
вычисления функции y = f ( x) |
в точке |
||
x + ∆x , т.е. имеем |
|
′ |
(1.21) |
|
f (x + ∆x) ≈ |
||||
f ( x) + f ( x) ∆x |
||||
Пример 1.15. Вычислить приближенно 
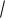 16,06 .
16,06 .
Решение. Рассмотрим функцию y =
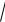 x . По формуле (1.21) имеем:
x . По формуле (1.21) имеем:
|
|
|
≈ |
|
+ ( |
|
)′ ∆x = |
|
+ |
∆x |
|
. |
|||
|
x + ∆x |
x |
x |
x |
|||||||||||
|
|
|
|
||||||||||||
|
|
2 x |
|||||||||||||
Так как x =16, ∆x = 0,06 , то получаем |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
≈ 4 + |
0, 0 8 |
= 4 , 0 1 . |
|
|
|
|
|||||
|
|
|
1 6 ,0 8 |
|
|
|
|
||||||||
|
|
|
2 4 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисления на калькуляторе дают значение 4,0099875 . Абсолютная погрешность составляет около 0,0000121.
Инвариантность формы записи дифференциала
Выше была установлена форма записи дифференциала dy = y′x dx в случае,
когда х является независимой переменной. Покажем, что данная форма имеет место и в том случае, когда х является функцией от произвольной переменной t.
В самом деле, если |
y = f ( x) и x = ϕ(t) , и тогда дифференциал dy находится по |
|||||
формуле |
|
|
|
|
dy = yt′dt |
(1.22) |
|
|
|
|
|
||
Используя |
правило |
дифференцирования сложной |
функции, можно |
|||
′ |
′ |
′ |
′ |
′ |
(t ) .Отсюда и (1.22) имеем |
|
записать yt |
= yx |
xt = yx |
ϕ |
|
||
|
|
|
|
|
dy = y 't x 't ∆t |
(1.23) |
Но x 't ∆t = dx . Окончательно из (1.23) имеем dy = y 't dx , |
а это означает, что |
|||||
форма записи дифференциала dy сохраняется независимо от того, является ли х независимой или зависимой переменной. Это свойство называют инвариантностью (неизменностью) формы записи дифференциала.
Особо |
следует отметить, что форма записи |
дифференциала в |
виде |
dy = y 't ∆x |
верна только в том случае, когда х – независимая переменная. Если |
||
же аргумент x является зависимой переменной, |
например, x = ϕ(t) , |
то, |
|
очевидно, что ∆x и dx не совпадают.
77
§1.6. Производные и дифференциалы высших порядков
|
Пусть |
функция |
|
y = f ( x) |
определена на |
интервале |
(a,b) |
и |
||||||||||||||||||||
дифференцируема |
|
в |
|
каждой |
точке этого |
|
|
интервала, |
|
т.е. |
|
|
для любого |
|||||||||||||||
x |
(a,b) существует |
y |
′ |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= f (x) . Тогда эту производную можно рассматривать |
|||||||||||||||||||||||||||
как |
функцию независимого |
переменного |
|
х |
и |
|
тем самым |
ставить |
вопрос |
о |
||||||||||||||||||
производной для функций y |
′ |
= |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
f (x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Производную от производной будем называть второй производной или |
|||||||||||||||||||||||||||
производной |
второго |
порядка |
исходной |
|
|
функции |
y = f ( x) . |
Вторую |
||||||||||||||||||||
производную будем обозначать либо y′′, либо |
f ′′( x) . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
1 |
|
′ |
|
|
2x |
|
|
|
|
|
|
|
Например, для функции y = arctg x |
имеем: |
|
|
|
|
2 |
= − |
|
|
|
|
|
2 . |
|
|
|||||||||||||
y = |
1+ x |
|
|
|
|
) |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ x |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
Аналогично |
производная |
от |
второй |
|
производной |
y |
′′ |
|
′′ |
|
|
|
|
||||||||||||||
|
|
|
= f (x) называется |
|||||||||||||||||||||||||
третей производной или производной третьего порядка функции |
y = f ( x) |
и |
||||||||||||||||||||||||||
обозначается либо y |
′′′ |
, либо f |
′′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Производной |
порядка |
|
(n +1) |
называется |
|
производная |
от |
|
производной |
||||||||||||||||||
порядка n. Эти производные обычно обозначаются специальным образом |
|
|||||||||||||||||||||||||||
|
|
|
|
y(4) = f (4) (x), |
y(5) = f (5) (x), ... , y(n) = f (n) (x) . |
|
|
|
|
|
|
|||||||||||||||||
|
Порядок производной берется в скобках, чтобы производную n-го порядка |
|||||||||||||||||||||||||||
y(n) |
отличить от n-ой степени функции yn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Рассмотрим функцию y = f ( x) , заданную на интервале (a,b) и пусть эта |
|||||||||||||||||||||||||||
функция имеет все производные вплоть до порядка n. |
|
Если |
∆x = dx |
– |
||||||||||||||||||||||||
приращение аргумента х, то выражение d n y , определяемое равенством |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dn y = y(n) (dx)n , |
|
|
|
|
|
|
|
|
|
|
|
||||||
называют дифференциалом n-го |
порядка. |
|
Обычно |
|
используют |
обозначение |
||||||||||||||||||||||
(dx)n = dxn , в этом случае дифференциал порядка n записывается в виде |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d n y = y(n)dxn |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Из последнего равенства можно формально написать, что |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y(n ) = |
d n y |
|
|
|
|
|
|
|
|
|
|
|
|
(1.24) |
|||
|
|
|
|
|
|
|
|
|
|
|
dxn |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Правая часть (1.24) обычно используется для выражения n-ой производной функции y = f ( x) .
Для закрепления материала решите самостоятельно следующие примеры и задачи.
Найти производные функций:
1.1. |
y = 11x2 + 6 x + 9 ; |
1.2. |
y = 5x4 + 6 x3 + 8 x + 9 ; |
1.3. |
y = 12 x2 + 5 x + 6 ; |
1.4. |
y = a x +1 + xa+1 |
78

1.5. |
y = cos 3x tg 7x ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1.7. |
y = |
cos 3x |
|
− sin |
|
π |
; |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
tg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
; |
|
|
|
|
|
||
1.9. |
y = 7 2x −1 + |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x − |
1 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.11. |
y = arcsin (cos x2 ); |
|
|
|
|
|
|
|
|
||||||||||||||||||||
1.13. |
y = arccos (sin x ) ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1.15. |
y = sin (cos (tg x )) ; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
1.17. |
y = ln |
|
e x |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 + ex |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1.19. |
y = x2 sin x lg x . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1.21. |
y = 25sin x ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1.23. |
y = |
|
|
3 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
log 2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1.25. |
y = |
log32 x |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.27. |
y = ln |
e x |
+1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ex |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
1.29. |
y = |
|
1 + x |
|
+ 3 x |
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
− x x 4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y = ln (x + |
|
|
); |
|
||||||||||||||||||||||||
1.31. |
1 + x2 |
|
|||||||||||||||||||||||||||
|
y = ln ( |
|
|
|
|
|
|
); |
|
|
|
|
|||||||||||||||||
1.33. |
1 + e2 x |
+ e4 x |
|
|
|||||||||||||||||||||||||
|
y = (x −1) |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1.35. |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1.37. |
y = (ln (x −1))x ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
||||||||
1.39. |
y = ln 5 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||||
e |
5 x |
|
− e |
−5 x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1.6. |
y = 3 |
ctg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1.8. |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y = sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1.10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y = 3 1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x +1 |
|
|
||||||||||||||||||||||||
1.12. |
y =(sin x +cos x)3 |
|
|
||||||||||||||||||||||||||
1.14. |
y = arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
ctg x |
|
|
||||||||||||||||||||||
1.16. |
y = arctg |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1.18. |
y = 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
tg (6 x) +1; |
|
|
|||||||||||||||||||||||||||
1.20. |
y = |
|
|
|
|
tg x ln x |
|
|
|||||||||||||||||||||
|
|
x |
|
|
|||||||||||||||||||||||||
1.22. |
|
|
|
ln2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y = 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1.24. |
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
log3 x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1.26. |
y = 3x x4 + 3 |
|
|
|
|
|
|||||||||||||||||||||||
|
π |
|
|
||||||||||||||||||||||||||
1.28. |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y = e |
|
|
|
|
arctg2 x; |
||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
3 |
|||||||||||||||||||||||||||||
1.30. |
y = |
1 |
|
|
|
|
|
|
|
|
|
|
x +1 |
|
|
||||||||||||||
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
− 2x |
||||||||||||||||||
1.32 |
y = ln (e2 x +1)− 2arctg(ex ); |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|||||
|
|
x |
|
sin3 |
( x |
||||||||||||
1.34. |
y = arctg |
|
|
|
|
|
|
|
|
|
+ 2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 x |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.36. |
y = |
|
sin x ; |
|
|
|
|
|
|
|
|||||||
x |
|
|
|
|
|
|
|
||||||||||
1.38. |
y = (arctg x)arcsin x |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1− x |
|
|
x2 |
+2 |
|
|||||||
1.40. |
y = arccos |
|
|
|
|
|
|
|
|
− e |
|
|
|
; |
|||
|
|
1+ x |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
79
Глава 2. Основные теоремы дифференциального исчисления
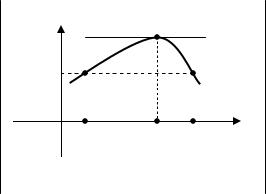
§2.1. Теорема Ролля
Многие приложения производной основаны на теореме Лагранжа о конечных приращениях функции. Эта теорема будет доказана ниже. Для её доказательства используется теорема Ролля о нуле производной, которая формулируется следующим образом:
Теорема 2.1 (Ролля). Пусть функция y = f (x) определена и непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), тогда, если на концах отрезка функция принимает равные значения, то существует точка c,
принадлежащая |
(a,b), в которой производная функции f (x) равна нулю, |
т.е. f ′(c) = 0 . |
Так как функция f (x) непрерывна на отрезке [a,b], то она |
Доказательство. |
достигает на этом отрезке своего наибольшего и наименьшего значения, которые обозначим соответственно M и m. При этом возможны два случая: M = m или M и m не равны.
1) если |
M = m , |
то y = f (x) |
– |
постоянная величина, следовательно, |
|||
f ′(x) = 0 во всех точках отрезка [a,b] |
, т.е., |
|
|
||||
y |
|||||||
в качестве |
точки c |
можно взять |
любую |
||||
|
|
||||||
точку из интервала (a,b).
2) если M и m не равны, то функция |
|
|
|
|
|
|
|
y = f (x) не является постоянной. Согласно |
|
|
|
|
|
|
|
условию теоремы f (a) = f (b) , поэтому хотя |
|
a |
|
с b |
x |
||
бы одно из значений M или m функция |
|
|
|||||
|
|
Рис.2.1 |
|
|
|||
принимает во внутренней точке интервала |
|
|
|
|
|||
(a,b). Не уменьшая общности, можно |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
предположить, что f (c) = m , где a < c < b . Найдём производную функции |
f (x) |
||||||
в точке c. По определению |
f (c + ∆x) − f (c ) |
|
|
|
|||
f '(c) = lim |
. |
(2.1) |
|||||
|
|
||||||
∆x→0 |
|
∆x |
|
|
|
|
|
Так как в точке a= c функция f (x) достигает своего минимума, то при любом
значении |
∆x |
всегда выполняется неравенство |
|
|
||||||
|
|
|
|
f (c + ∆x) − f (c) > 0 . |
|
(2.2) |
||||
Если ∆x |
> |
0, |
то |
f (c + ∆x) − f (c) |
> 0 и, следовательно, |
согласно (2.1), |
||||
|
||||||||||
|
|
|
|
∆x |
f (c + ∆x)− f (c) |
|
|
|||
f ′(c) ≥ 0 . |
Если |
же |
∆x < 0, то |
< 0 и, |
следовательно, |
|||||
|
∆x |
|
||||||||
|
|
|
|
|
|
|
|
|||
f ′(c) ≤ 0 .
80
