
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник
.pdf
y |
|
|
y = f(x) |
|
|
0 |
4 |
x |
|
||
|
|
y = f(x–4) |
|
Рис. 2.4 |
|
y = f(x) |
|
|
y = f(0,5x) |
1 |
2 |
0 |
|
Рис. 2.5 |
|
Функция может быть задана в виде таблицы. Например, измеряя температуру воздуха в течение суток через каждый час, мы получим таблицу, которая соответствует функции T = f (t) .
t |
0 |
1 |
… |
24 |
|
|
|
|
|
T |
T0 |
T1 |
… |
T24 |
|
|
|
|
|
Итак, мы определили три типа задания функции. Очевидно, что для функции, заданной формулой, можно построить и соответствующий ей график и таблицу.
Решение обратной задачи – по графику функции восстановить её формулу
– не всегда вполне определено. Как для функции, заданной графически или таблично, выписать формулу, ее выражающую? Возникает вопрос: а что называть формулой? В частности, вкладывать ли в понятие формулы только конечное число действий?
Во всяком случае, для нас важно, что каким бы из перечисленных выше способов функция ни была бы задана, она является объектом изучения математического анализа.
§2.2. Простейшие свойства функций
Процесс изучения функций состоит в исследовании ее поведения при изменении независимой переменной. Всюду в дальнейшем предполагается, что независимая переменная изменяется, возрастая и принимая все промежуточные значения. Расширяя наши познания, мы будем давать, все более подробное описание функции. Свои исследования начнём, используя только элементарные свойства, доступные из школьного курса математики. Рассмотрим следующие простейшие свойства функции:
1.Наличие нулей;
2.Четность и нечетность;
3.Периодичность;
4.Рост и убывание.
21
Остановимся подробнее на каждом из этих свойств.
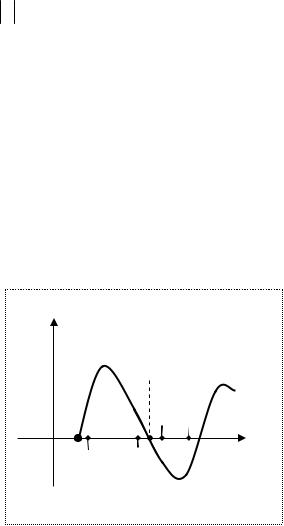
Определение 2.2. Если f (x0 ) = 0 , то число x0 называют нулем функции.
Если для всех x (a,b) функция f (x) положительна ( f (x) > 0 ), то на
данном интервале график функции находится выше оси абсцисс; если же для всех x (c, d ) функция f (x) отрицательна, то на интервале (c, d ) график
функции f (x) находится под осью абсцисс (рис.2.6). В нулях функции график пересекает ось абсцисс или касается её.
Определение 2.3. Функция y = f (x) называется четной, если для всех значений х из области определения выполняется равенство f (−x) = f (x) ;
функция называется нечетной, если для всех значений х из области определения выполняется равенство f (−x) = − f (x) .
Отметим, что область определения как четных, так и нечетных функций симметрична относительно начала системы координат.
Так функция y = x2 является четной. Если же рассматривать эту же функцию y = x2 , но заданную, например, только на интервале (0;1), то она
четной уже не является.
Примерами четных функций, заданных на всей числовой оси, служат также функции y = cos x , y = sin (x2 ), y = x . Примерами нечетных функций служат функции y = 3x , y = tg x . Отметим, что функция не обязательно должна
быть четной |
или нечетной. Например, функции y = x2 + 2x , y = ex , |
y = sin x + cos x |
не являются ни четными, ни нечетными. Такие функции будем |
называть функциями общего вида.
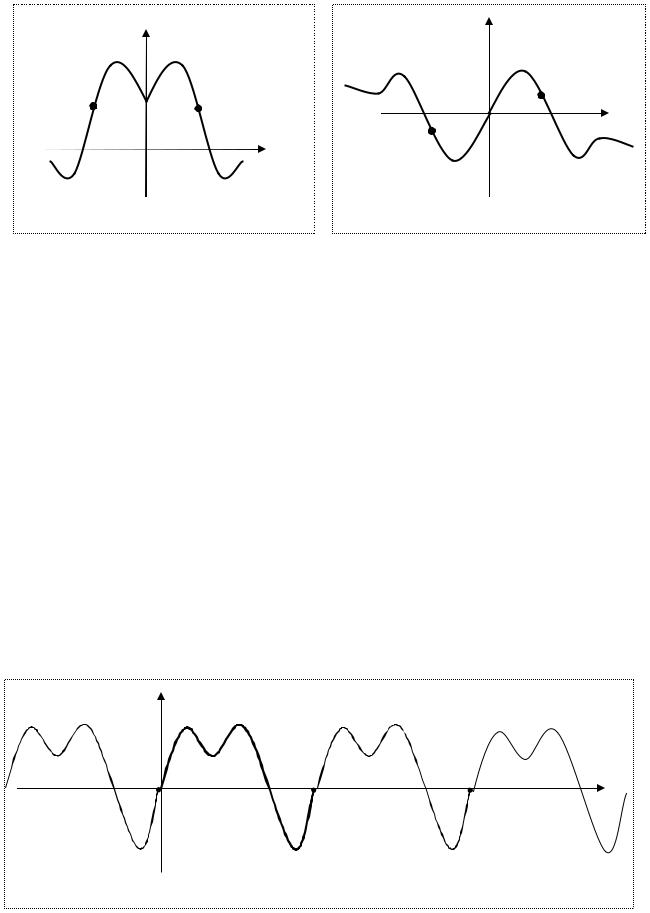
Отметим, что графики четных функций симметричны относительно оси Oy (рис.2.7); график любой нечетной функции симметричен относительно
начала координат (рис.2.8). В самом деле, пусть точка M (x, y) принадлежит графику четной функции y = f (x). Точка M ′(−x, y) симметричная точке M относительно оси Oy также принадлежит графику этой функции в силу того,
что |
f (−x) = f (x) = y . Соответственно, |
|
||||
если точка M (x, y) принадлежит графику |
y |
|||||
нечетной |
функции, |
то |
симметричная |
|||
относительно начала |
координат |
точка |
x0 |
|||
M ′′(−x,−y) |
также |
лежит |
на |
кривой |
||
y = f (x), так как f (−x) = − f (x) = −y .
|
с d |
x |
|
a |
b |
||
|
|||
|
Рис. 2.6 |
|
22
|
y |
y |
|
|
|
||
M' |
M |
M |
|
x |
|||
|
|
||
|
x |
M'' |
|
Рис. 2.7 |
|
|
|
Рис. 2.8 |
|
Определение 2.4. Функция |
y = f (x) |
называется |
периодической, |
если |
||
существует |
такое число |
t ≠ 0 , |
что для |
любого x из области определения |
||
функции |
x + t также |
принадлежат области определения и при |
этом |
|||
f (x + t) = f (x) . |
|
|
|
|
|
|
Число t называется периодом функции y = f (x). |
Совершенно очевидно, |
|||||
что если t - период, то числа 2t , 3t , −t , −2t также являются периодами. В самом деле, например,
f (x + 2t) = f ((x + t) + t) = f (x + t) = f (x) ; f (x − 2t) = f ((x − 2t) + 2t) = f (x) .
Вообще, если t |
период, то и kt |
также период при любом k : |
f (x + kt) = f (x) . Таким |
образом, всякая |
периодическая функция имеет |
бесконечно много периодов.
Учитывая это и говоря о периоде функции, мы будем иметь в виду наименьшее положительное число T для которого выполняется равенство
f (x +T ) = f (x) .
Примерами периодических функций являются тригонометрические функции y = sin x , y = cos x , y = tg x , y = ctg x . Первые две из них имеют
период 2π, вторые две – период π. y
x
O
Рис. 2.9
Особо следует отметить, что если периодическая функция с периодом T не определена в точке x0 , то она не определена во всех точках x0 + kT ,
23
k = 0, ±1, ±2,... Например функция y = tg x не определена в точках |
π |
+ kπ; а |
y = ctg x в точках kπ, k = 0, ±1, ±2,... |
2 |
|
|
|
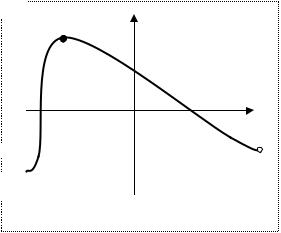
Для построения графика периодической функции, достаточно построить
его на интервале [x0 , x0 +T ], а затем повторить ось с периодом Т (рис.2.9). 
Определение 2.5. Функция называется возрастающей на интервале, если для любых двух значений аргумента из этого интервала большему значению аргумента соответствует большее значение функции.
Функция называется убывающей на  А интервале, если большему значению
А интервале, если большему значению 
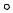 аргумента соответствует меньшее
аргумента соответствует меньшее  значение функции.
значение функции.
Итак, функция y = f (x) возрастает на
этот график на всю числовую
B y
x
C
Рис. 2.10
интервале (a,b) , если |
для любых x1, x2 (a,b) , таких что x1 < x2 |
вытекает |
f (x1 ) < f (x2 ) . |
если для любых x1, x2 (a,b) , таких что x1 < x2 |
|
Функция убывает, |
вытекает |
|
f (x1 ) > f (x2 ) . Если рассматривать график возрастающей функции |
(рис.2.10) |
|
слева направо (т.е. по возрастанию аргумента), то график поднимается вверх (дуга AB), для убывающей функции график опускается вниз (дуга BC).
Интервал изменения аргумента, в котором функция возрастает, называется интервалом возрастания, а интервал, в котором функция убывает, называется интервалом убывания. Интервалы возрастания и убывания функции называют интервалами монотонности.
Функцию y = f (x) называют неубывающей на интервале (a,b) , если для любых x1, x2 (a,b) таких, что x1 < x2 , вытекает нестрогое неравенство f (x1 ) ≤ f (x2 ) . Соответственно, функция называется невозрастающей, если для любых x1, x2 (a,b) таких, что x1 < x2 , выполняется нестрогое неравенство
f (x1 ) ≥ f (x2 ) .
При построении графиков функции выделяются интервалы возрастания и убывания функции, а также интервалы ее постоянства.
Если график функции известен, то нахождение интервалов монотонности не вызывает затруднения. Наша цель – научиться находить участки монотонности и в том случае, когда график функции неизвестен.
§2.3. Понятие обратной функции
Предположим, что задана функция |
|
y = f (x). |
(2.1) |
24
По определению функции, фиксируя значение переменной величины x, получаем соответствующее значение y . Спрашивается, возможно ли поменять
местами x и y , т.е. считать y - аргументом, а x - функцией? Но тогда уравнение (2.1) определяет x, как неявную функцию y . В этом случае функция x от переменной y называется обратной по отношению к исходной функции.
Если уравнение (2.1) разрешимо относительно x, то можно получить явное выражение обратной функции
x = ϕ( y) . |
(2.2) |
При этом функция ϕ( y) для всех допустимых значений |
y удовлетворяет |
условию: f (ϕ( y)) = y . |
|
Например, в формуле пройденного пути свободно падающего тела
S = gt22
время t - аргумент, а S - функция. Разрешив это уравнение относительно t , получим функцию, обратную данной функции.
t = |
2S |
. |
|
||
|
g |
|
В общем случае, если придерживаться стандартных обозначений и обозначать независимую переменную x, а функцию y , то обратную функцию
нужно записать в виде
y = ϕ(x) .
Функции y = f (x) и y = ϕ(x) - взаимно обратные. Например, функции
y = 2x и y = log2 x взаимно обратные.
Обратную функцию, в нашем понимании, может иметь только монотонная функция. В некоторых случаях для получения обратной функции вводят дополнительные ограничения на ее возможные значения. Например,
неоднозначная функция x = ±
 y является обратной для функции y = x2 . Если условиться, что берётся лишь арифметическое значение корня, то обратная
y является обратной для функции y = x2 . Если условиться, что берётся лишь арифметическое значение корня, то обратная
|
|
функция будет однозначной. |
|
|
||||
|
y |
Часто |
используется |
обозначение |
||||
|
y = f −1 |
(x) |
для |
функции, |
обратной |
к |
||
|
|
|||||||
|
|
функции y = f (x). |
|
|
|
|||
y= |
x |
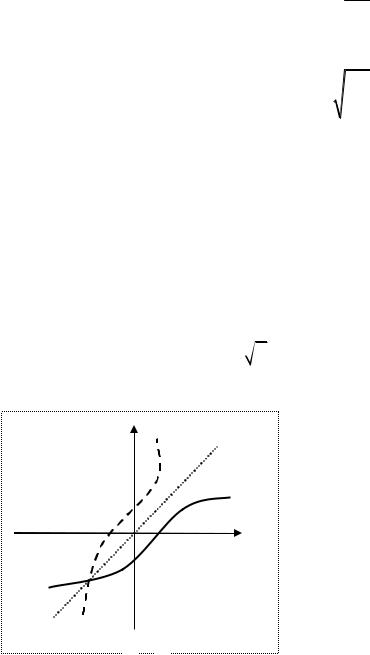
Особо следует отметить, что одна и та |
||||||
же кривая представляет собой как график |
||||||||
|
||||||||
|
(x) |
прямой |
функции, |
так и обратной. Все |
||||
|
зависит от того, на какой оси – Ox или Oy |
|||||||
|
|
|||||||
|
|
– выбирается аргумент. |
|
|
||||
|
|
Если прямую и обратную функции |
||||||
|
Рис. 2.11 |
считать |
функциями одного |
аргумента |
x, |
|||
|
|
т.е. рассматривать |
функции |
y = f ( x) |
и |
|||
25

y = ϕ(x) , то график одной этих функций есть зеркальное отображение графика другой функции относительно биссектрисы I и III координатных углов, т.е. прямой y = x (рис.2.11). В самом деле, если точка M (x, y) лежит на графике одной из этих функций, то тогда симметричная относительно указанной биссектрисы точка N ( y, x) непременно лежит на графике другой.
§2.4. Элементарные функции
Для определения элементарных функций нам потребуются хорошо известные из школьного курса функции, которые называют простейшими или
основными элементарными функциями. К ним относятся:
•степенная функция y = xa ;
•показательная функция y = ax , a > 0, a ≠ 1;
•логарифмическая функция y = loga x , a > 0, a ≠ 1;
•тригонометрические функции y = sin x; y = cos x; y = tg x; y = ctg x ;
• обратные тригонометрические функции y = arcsin x; y = arccos x; y = arctg x; y = arcctg x .
Для удобства дальнейшего изучения введем понятие сложной функции. Рассмотрим две функции (компоненты) y = f ( x) и y = g(x) . Пусть при этом
область определения функции y = f ( x) содержит область значений функции y = g(x) , т.е. E (g ) D( f ). Тогда можно рассматривать функцию y = f (g (x)),
которую называют композицией (суперпозицией) функций f (x) и g( x) .
Заметим, что и область определения, и область значений такой функции от функции может не совпадать с соответствующими областями компонент. Будем называть сложной функцией всякую композицию основных
элементарных функций. Например, для двух функций y = x2 и y = sin x можно
получить две сложных функции: y = sin (x2 ) |
и y = sin2 x . Другой пример: имея |
||||||||
функции y = |
|
и y = tg x , получим из них композиции y = |
|
|
и y = tg |
|
. |
||
x |
x |
||||||||
tg x |
|||||||||
Разумеется, функции-компоненты могут совпадать. Так, например, для |
|||||||||
функции y = ln x , можно рассматривать |
сложные функции |
y = ln (ln x), |
|||||||
y = ln (ln (ln x)) и т.д.
Определение 2.6. Элементарной функцией называется функция, полученная из простейших функций с использованием конечного числа арифметических действий и конечного числа операций композиции (взятия функции от функции).
Остановимся более подробно на простейших элементарных функциях, достаточно полно изученных в курсе средней школы.
26
• |
Степенная функция y = xn . |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y=x2 |
|
|
|
|
|
|
|
y=1/x2 |
|
y=1/x3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
y=x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=1/x |
|
|
|
|
|
||
|
|
|
y=x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.12 |
|
|
|
|
|
Рис. 2.13 |
|||||
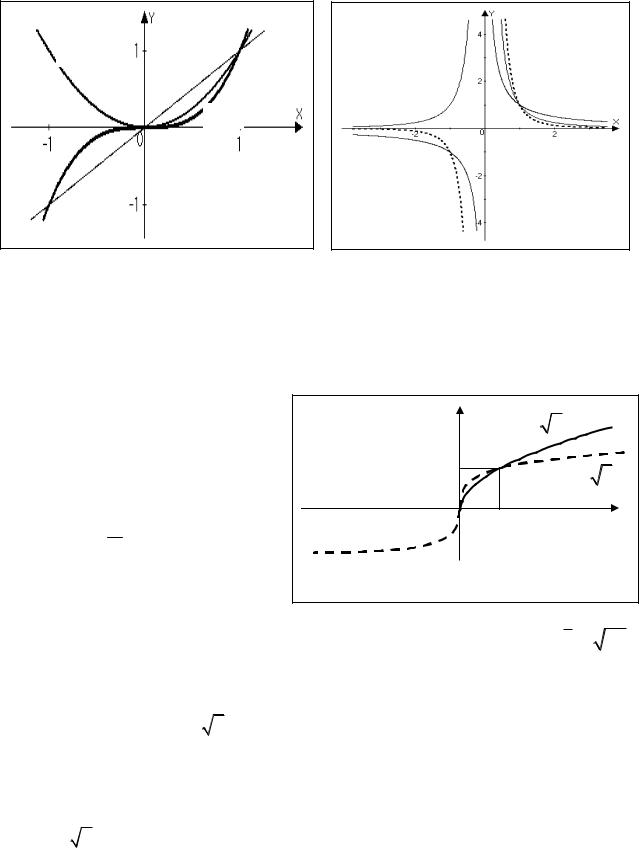
Рассмотрим вначале случай, когда n – |
целое число. Если n > 0 , |
то функция |
|||||||||||||||
y = xn |
определена на всей числовой оси. В этом случае графиками функции |
||||||||||||||||
являются: |
при n =1 |
– |
прямая |
линия, |
при |
n = 2 – |
парабола, |
при |
n = 3 – |
||||||||
кубическая парабола и т.д. На рис.2.12 приведены некоторые из этих графиков. |
|||||||||||||||||
|
Если |
n < 0 , |
то |
областью |
определения |
|
функции |
y = xn |
является вся |
||||||||
числовая ось за исключением точки |
|
|
|
|
|
|
|
|
|
||||||||
x = 0 . |
В |
этом случае |
графиками |
|
|
|
y |
y = |
x |
|
|||||||
являются |
гиперболы |
различных |
|
|
|
|
|
|
|
|
|
||||||
порядков. Часть из них приведена |
|
|
|
|
1 |
|
|
|
|
||||||||
на рис.2.13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Рассмотрим |
теперь |
случай, |
|
|
|
|
0 |
|
|
|
|
|||||
когда |
|
n = p |
|
– |
дробное |
|
|
|
|
1 |
|
|
x |
||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рациональное число ( p и q целые |
|
|
|
Рис. 2.14 |
|
|
|
||||||||||
числа, |
q > 0 ). |
Тогда |
степенная |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
y = xn |
|
|
|
|
|
|
|
|
|
|
|
|
p |
= q x p . |
функция |
определяется |
|
следующим |
образом: |
y = xn = x q |
||||||||||||
Областью |
определения |
такой |
функции является при |
p > 0 |
бесконечный |
||||||||||||
интервал |
0;+∞) , |
а |
при |
p < 0 |
интервал |
|
(0,+∞). |
Наибольший |
интерес |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
представляет радикал y = n x , где n- натуральное число. Областью определения |
|||||||||||||||||
такой функции при четном n является множество всех неотрицательных чисел |
|||||||||||||||||
0;+ ∞), а при нечетном n - вся числовая ось (−∞, +∞) . Так как функция x = yn |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
является обратной для функции |
y = xn , |
то графиками радикалов, т.е. функций |
|||||||||||||||
вида |
|
y = n x , являются либо параболы различных нечетных порядков, либо |
|||||||||||||||
части парабол четных порядков. Графики некоторых таких функций приведены |
|||||||||||||||||
на рис.2.14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
27
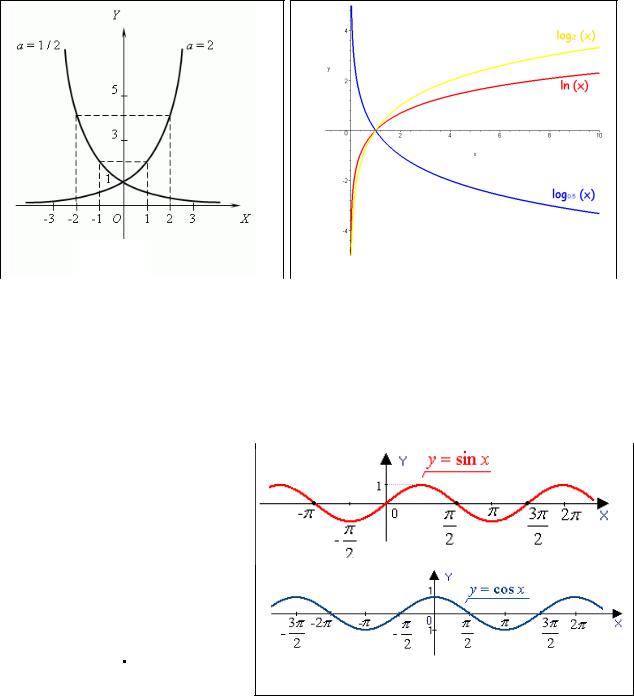
• Показательная функция y = ax , a > 0, a ≠1. Функция определена на всей
числовой оси. Значение этой функции всегда положительно, следовательно, ее график проходит над осью абсцисс. При любом значении a график функции
всегда проходит через точку M0 (0;1), ввиду того, что a0 =1. При a >1,
функция возрастает и при 0 < a <1 – убывает. На рис.2.15 приведены графики показательной функции.
y = ax
|
Рис. 2.15 |
|
|
|
Рис. 2.16 |
|
|
|
|
|
|
|
|
|
|
|
|
Логарифмическая |
функция |
y = loga x, a > 0, a ≠ 1 . |
Функция |
определена при |
||||
x (0, ∞) . Если |
y = loga x , |
то, по определению, |
x = a y . |
Таким образом, |
||||
логарифмическая функция является обратной по отношению к показательной. Отсюда вытекает, что график логарифмической функции получается из графика показательной функции с помощью зеркального отображения последнего
относительно |
прямой |
y = x |
|
||
(рис.2.16). |
|
|
|
|
|
|
|
|
|
|
|
• Тригонометрические |
|
|
|||
функции |
y = sin x , |
y = cos x , |
|
||
y = tg x , y = ctg x . |
|
|
|
||
Аргументом |
|
этих |
|
||
функций являются, в нашем |
|
||||
случае, |
числа, |
которые |
|
||
рассматриваются как |
меры |
|
|||
угла, выраженные в радианах. |
|
||||
Рассмотрим |
каждую |
из |
|
||
приведенных |
выше |
функций |
Рис. 2.17 |
||
подробнее.
Функция y = sin x имеет областью определения всю числовую ось и
обладает областью значений |
[ |
] |
sin x |
|
≤1. Эта функция периодическая |
|
−1;+1 , т.е. |
|
|||
с периодом 2π. Равенство |
|
sin x = sin(x + 2π) выполняется при любом x. |
|||
Графиком функции y = sin x является синусоида (рис.2.17).
28
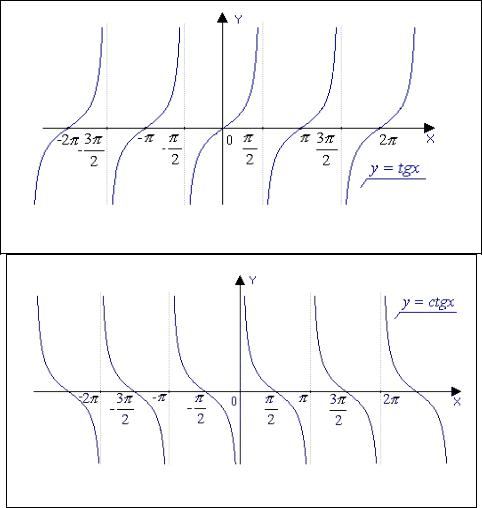
Функция |
|
y = cos x , также определена на всей числовой оси и также верно |
||||||
неравенство |
|
cos x |
|
≤1. Графиком функции |
является |
косинусоида, |
которая |
|
|
|
|||||||
представляет |
|
собой синусоиду, сдвинутую |
влево на |
величину |
π. |
График |
||
функции y = cos x приведен на рис.2.17. |
|
|
2 |
|
||||
|
|
|
|
|||||
Функция |
|
y = tg x не определена при x = π + kπ , |
где k = 0, ±1, ±2,... . Эта |
|||||
|
|
|
|
|
2 |
|
|
|
функция имеет период, равный π. При приближении слева к значению x = π2
функция y = tg x неограниченно растёт, а при приближении справа к значению x = − π2 она неограниченно убывает.
График функции приведен на рис.2.18.
Функция y = ctg x не определена при x = kπ, где k = 0, ±1, ± 2,... . Функция имеет период, равный π. При приближении слева к значению x = 0 функция y = ctg x неограниченно убывает, а при приближении справа к значению x = π она неограниченно возрастает.
График этой функции изображен на рис.2.19.
Рис. 2.18
Рис. 2.19
29
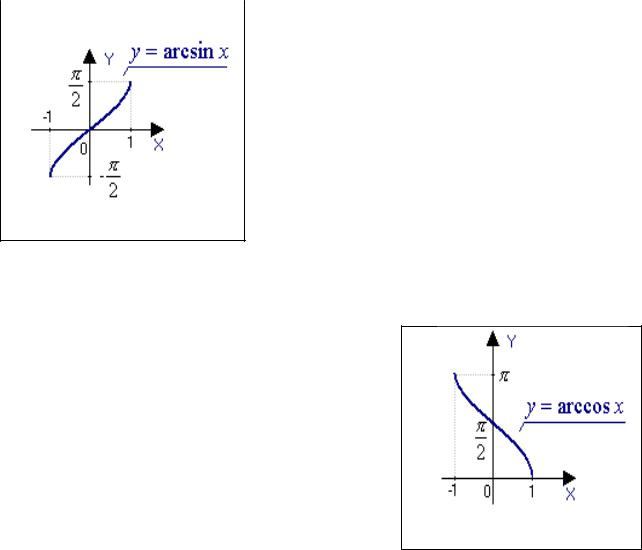
• Обратные тригонометрические функции y = arcsin x , y = arccos x , y = arctg x , y = arcctg x . Рассмотрим каждую из этих функций.
Функция |
y = arcsin x |
имеет областью определения отрезок |
[ |
|
|
] |
|||||||
|
−1;+1 , и по |
||||||||||||
определению |
y = arcsin x |
– это дуга, |
взятая в пределах области определения |
||||||||||
функции, синус которой равен x, |
т.е. |
sin y = x . Отсюда следует, |
что значение |
||||||||||
|
|
|
y |
изменяется в |
пределах |
от − |
π |
до |
π, т.е. |
||||
|
|
|
2 |
||||||||||
|
|
|
− π |
≤ y ≤ π . |
|
|
|
|
|
2 |
|||
|
|
|
Эти |
значения |
функции |
называют |
|||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
главными значениями функции. |
|
|
|
sin y = x |
||||||
|
|
|
|
Если |
решить |
уравнение |
|
||||||
|
|
|
относительно неизвестной |
величины |
y , то |
||||||||
|
|
|
полученное решение является многозначным. В |
||||||||||
|
|
|
этом случае пишем |
y = Arcsin x . |
|
График этой |
|||||||
функции есть не что иное, как синусоида, Рис. 2.20 идущая вдоль оси ординат (рис.2.20). Нетрудно
видеть, что справедливо равенство
Arcsin x = (−1)k arcsin x + kπ, k = 0, ±1, ± 2,...
Функция y = arccos x имеет областью
определения |
отрезок |
[ |
−1; |
] |
а |
область |
|||
|
+1 , |
||||||||
значений |
есть |
отрезок |
|
[ |
0; |
] |
т.е. |
главные |
|
|
|
π , |
|||||||
значения |
функции |
заключены |
в |
пределах |
|||||
0 ≤ arccos x ≤ π. |
По |
определению, |
функция |
||||||
y = arccos x – это дуга, |
косинус которой равен |
x, т.е. справедливо |
равенство cos y = x . |
Разрешая последнее уравнение, имеем, по определению, y = Arccos x .
График этой функции изображен на рисунке 2.21.
Справедлива формула
Arccos x = ±arccos x + 2kπ,
Рис. 2.21
k = 0, ±1, ±2,...
Функция |
y = arctg x , по определению, есть дуга в пределах |
|
− |
π |
, |
π |
, |
|
2 |
|
|||||
|
|
|
|
|
2 |
|
тангенс которой |
равен x, т.е. |
tg y = x Решение полученного |
уравнения |
относительно y |
дает многозначную функцию y = Arctg x . Имеет место |
||
равенство Arctg x = arctg x + kπ. |
Функция y = arctg x имеет |
областью |
|
30
