Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Телекоммуникаций и Информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник

.pdf

Скачиваний:

103

Добавлен:

11.04.2015

Размер:

2.86 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1612 13 14 15 16 > Следующая >>>

РАЗДЕЛ III. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Глава 1. Основные понятия и свойства функции нескольких переменных

§1.1. Понятие функции нескольких переменных

Большинство физических величин являются зависимыми от других величин, причём, как правило, от нескольких. Например, температура может изменяться при переходе от одной точки к другой. Поскольку каждая точка определяется тремя декартовыми координатами, допустим x, y, z, то и температура определяется значениями трех переменных x, y и z. Сила притяжения между двумя телами зависит от их масс и расстояния между ними.

Настоящая глава посвящена функциям многих переменных. Изучение функций многих переменных ограничим случаем, когда функция зависит от двух переменных. Этот важный частный случай выявит все важнейшие особенности функций многих переменных. Отметим, что для функции двух переменных допустима наглядная геометрическая интерпретация.

Если на плоскости введена система координат, то каждая точка M плоскости характеризуется двумя числами – координатами x и y. Сопоставив каждой такой точке действительное число z, мы тем самым определим

функцию

z = f (M )

или

z = f (x, y ) –

функцию

двух независимых

переменных.

Пример 1.1.

z = x2 − y2 ,

Пример 1.2.

z =

sin

x2 + y2

z = e−

x2 + y2

Пример 1.3.

z = 1− x2 − y2

Пример 1.4.

Множество

D = D ( f )

всех

точек M (x; y ) , для которых значение

функции

z = f

(x, y )

определено,

называется

её

областью определения. В

примере 1.1 областью определения служит вся плоскость, в примере 1.2 – вся плоскость за исключением точки (0;0) , в примере 1.3 – круг радиуса 1 с центром в начале координат, а в примере 1.4 – также вся плоскость за исключением точки (0;0) .

Графиком функции двух переменных служит поверхность в трёхмерном пространстве. Каждая точка этой поверхности имеет координаты

{x; y; f (x, y )}.

Графики для примеров 1.1- 1.4 показаны соответственно на рис.1.1 - 1.4. Для определения функции трёх переменных необходимо рассмотреть

множество V точек трёхмерного пространства, характеризуемых в случае введённой системы координат, тремя числами x, y, z . Пусть M (x; y; z ) V .

111

Рис. 1.1

Рис. 1.3

Рис. 1.2

Рис. 1.4

Сопоставим каждой такой точке некоторое действительное число. Тем самым определена функция трёх независимых аргументов u = f (x, y, z ) . Для

изображения такой функции требуется уже четырёхмерное пространство.

В общем случае, функцией n независимых переменных называется правило, при котором каждой упорядоченной совокупности n чисел (x1 , x2 ,…, xn ) ставится в соответствие некоторое число у. Будем использовать в

этом случае обозначение y = f (x1 , x2 ,…, xn ).

Вернёмся к случаю двух переменных. Ещё одним примером такой

функции является расстояние от фиксированной точки

M 0 (x0 ; y0 )

до точки

M (x; y ) . Как известно,

расстояние от M 0

до

M определяется равенством

(M , M

) =

x − x

2 + y − y

, определенным для всех точек плоскости.

Назовём

δ-окрестностью точки M 0 (x0 ; y0 )

множество

точек,

удовлетворяющих

неравенству

ρ(M , M 0 ) < δ .

Очевидно, δ-окрестность

представляет

собой

внутренность

круга

радиуса δ

с центром

в точке

M 0 (x0 ; y0 ) .

112

Точка М называется внутренней точкой области D, если эта точка принадлежит области D вместе с некоторой своей δ-окрестностью.

Область D называется открытой, если все её точки – внутренние.

Точка М называется граничной точкой области D, если любая δ- окрестность этой точки содержит как точки области D, так и точки не входящие в эту область. Множество граничных точек области D образует её границу. На


рис.8.5 точка М1 – внутренняя точка, а
М2 – граничная точка области D1.
Замкнутым			называется			D1
множество, которое содержит все свои					δ	М2
граничные точки.					М1
			линейно
Область		называется
связной, если любые две её точки						D2
можно соединить ломаной, все точки
которой принадлежат этой области. На
рис.1.5 области D1 и D2 – связные.
Область D3 не связная.						D
В	дальнейшем,		если	не

предполагается		обратное,	будем	под		Риc. 1.5
областью	подразумевать		открытую
линейно связную область.

§1.2. Предел функции двух переменных

Пусть функция z = f (x, y ) определена в некоторой области, содержащей точку M 0 (x0 ; y0 ) . Число А называется пределом функции z = f (x, y ) в точке

M 0 (x0 ; y0 ) , если для любого положительного числа ε можно указать такое положительное число δ, что для всех точек M из δ-окрестности точки M 0 , за исключением может быть самой точки M 0 , выполняется неравенство

f (M ) − A < ε.

Будем записывать этот факт следующим образом:

lim f (x, y) = A или	lim f (M ) = A.	(1.1)
x→x0	M →M0
y→y0

Из определения предела следует, что если он существует, то он не зависит от способа стремления точки М к точке M 0 . Заметим, что для функции одной

переменной можно говорить о левостороннем или правостороннем пределах. Для функции двух переменных число таких «односторонних» пределов бесконечно. Это обстоятельство значительно отличает факт существования предела функции одной переменной от функции двух или большего числа переменных.

Пример 1.6. Найти предел lim	x 2	− y 2	.
x→ 0	x 2	+ y 2
y → 0

113

Решение. Пусть точка M (x; y ) приближается к точке O (0; 0) вдоль прямой y = kx . Тогда

lim

x 2 − y 2

= lim

x 2

− k 2 x 2

= lim

1 − k 2

1 − k

x 2 + y 2

x 2

+ k 2 x 2

1 + k 2

1 + k

x → 0

x→ 0

y → 0

Очевидно, при разных значениях k предел будет принимать разные значения.

Следовательно, функция z =

x2 − y 2

не имеет предела в точке O(0;0).

x2 + y 2

Пример 1.7. Найти предел

lim

+ y

y→∞ x

x→∞

Решение. Снова выберем путь стремления точки

(x; y )

к бесконечности вдоль прямой

y = kx , (k > 0 ) . В таком случае

		k k
Выражение
	2
k		+ 1

lim

x → ∞ y → ∞

< 1

xy xy

kx 2

k x 2

= lim

+ y

x→ ∞

+ 1) x

x →∞

+ 1

k x 2

при любом значении k. Но тогда lim

x → ∞

+ 1

= 0 .

Отметим, что	если lim f (x, y) = A, то при	A = 0 функция	f (x, y)	в
	x→x0
	y→y0
окрестности точки	(x0 ; y0 ) называется бесконечно	малой, а при	A = ∞	–

бесконечно большой. Кроме того, имеют место все свойства пределов, известные для функции одной переменной.

Свойство 1.1. Если пределы функций f (x, y) и g(x, y) при M (x; y ) , стремящемся к M 0 (x0 ; y0 ) , существуют и конечны, то предел суммы этих функций равен сумме пределов, т.е.

lim ( f (x, y) + g (x, y)) = lim f (x, y) + lim g (x, y) .
x→x0	x→x0	x→x0
y→y0	y→y0	y→y0
Свойство 1.2. Если пределы функций	f (x, y) и	g(x, y) при M (x; y ) ,

стремящемся к M 0 (x0 ; y0 ) , существуют и конечны, то предел произведения этих функций равен произведению пределов, т.е.

lim	( f (x, y) g (x, y)) = lim f (x, y) lim g (x, y) .
x→x0	x→x0	x→x0
y→y0	y→y0	y→ y0
Свойство 1.3. Если	пределы функций f (x, y)	и g(x, y) при M (x; y ) ,

стремящемся к M 0 (x0 ; y0 ) , существуют и конечны и, при этом, предел g(x, y)

отличен от нуля, то предел отношения этих функций равен отношению пределов, т.е.

			lim f (x, y)
	f (x, y)		x→x
lim	f (x, y)	=	y→y0	.
lim		=	0	.
x→x			0
y→y0	g(x, y)		lim g(x, y)
0			x→x0
			y→y0

114

Свойство 1.4. Если для всех точек некоторой окрестности точки M 0 (x0 ; y0 ) для функций f (x, y) и F (x, y) выполняется неравенство f (x, y) ≤ F (x, y) и пределы f (x, y) и F (x, y) при M (x; y ) → M 0 (x0 ; y0 ) существуют, то

lim f (x, y) ≤ lim F (x, y) .
x→x0	x→x0
y→y0	y→y0

Свойство 1.5. Если для всех точек некоторой окрестности точки M 0 (x0 ; y0 ) для функций f (x, y) , F (x, y) , Φ(x, y) выполняются неравенства

	Φ(x, y) ≤ f (x, y) ≤ F (x, y) .
Если при этом lim Φ(x, y) = lim F (x, y) = A , то предел f (x, y) существует
x→x0	x→x0
y→y0	y→y0

и также равен A : lim f (x, y) = A .

x→x0 y→y0

§1.3. Непрерывность функции двух переменных

Пусть точка M 0 (x0 ; y0 ) принадлежит области определения функции z = f (x, y ) вместе с некоторой окрестностью этой точки.

Определение 1.1. Функция z = f (x, y ) называется непрерывной в точке M 0 (x0 ; y0 ) , если ее предельное значение в этой точке существует и равно

значению f (M 0 ), т.е. lim f (M ) = f (M0 ).
M →M0
Точки, в которых не выполнено это определение, называются точками
разрыва функции. Например, у функций примеров 1.2 и 1.4 точка			O (0;0)
является точкой разрыва. А у функции z =	1	точки разрыва образуют целую
является точкой разрыва. А у функции z =	x − y	точки разрыва образуют целую
линию – прямую y = x .	x − y
линию – прямую y = x .
На языке « ε − δ » определение непрерывности примет следующий вид.
Определение 1.2. Функция z = f (x, y )	называется непрерывной		в точке

M 0 (x0 ; y0 ) ,

если для любого ε > 0 можно указать такое δ > 0 , что для всех

точек

таких,

что

ρ(M , M 0 ) ≤ δ ,

выполняется

неравенство

f (M ) − f (M0 )

< ε.

M 0 (x0 ; y0 )

Обозначим

приращение

функции

точке

∆z = f (M ) − f

(M 0 ) = f (x, y ) − f (x0 , y0 )

назовём

его

полным

приращением.

Обозначим

также

приращения

аргументов,

соответственно

x − x0 = ∆x и y − y0 = ∆y .

Тогда определение непрерывности функции двух переменных можно сформулировать так: функция непрерывна в точке M 0 , если полное приращение

115

функции в этой точке стремится к нулю, когда приращения аргументов стремятся к нулю

				lim ∆z = lim ∆z = 0 .
			M →M0		∆x→0
					∆y→0
Если положим		∆y = 0 ,	то функция		f (x0 + ∆x, y0 + ∆y ) = f (x0 + ∆x, y0 )
является	функцией	одной	переменной		x	(точнее ∆x ) и ее приращение
f (x0 + ∆x, y0 ) − f (x0 , y0 ) = ∆x z				называется		частным приращением функции
по x.
Аналогично, при ∆x = 0 f (x0 , y0 + ∆y )						– функция одной переменной y
(точнее	∆y ). Её	приращение		f (x0 , y0 + ∆y ) − f (x0 , y0 ) = ∆y z называется

частным приращением по y.

Определение 1.3. Функция z = f (x, y ) называется непрерывной по переменной x в точке (x0 ; y0 ) , если ее частное приращение ∆x z в этой точке стремится к нулю при стремлении к нулю ∆x . Аналогично, функция z = f (x, y ) называется

непрерывной по переменной y в точке (x0 ; y0 ) , если ее частное приращение

∆y z в этой точке стремится к нулю при условии ∆y → 0 .

Непрерывность по отдельным переменным, однако, недостаточна для непрерывности функции в точке. Убедимся в этом, рассматривая следующий пример.

			xy		, x	2	+ y	2	≠ 0
Пример 1.8. Докажем, что функция
		2	+ y	2
	z = x
			0		, x	2	+ y	2	= 0

непрерывна по каждой переменной в		отдельности							в точке O (0; 0) , но не является

непрерывной в этой точке при одновременном изменении координат. Поверхность, задаваемая этой функцией, представлена на рис. 1.6.

Рис. 1.6

116

Действительно, полагая, например,	y = 0 , получаем z (x, y ) = z( x) и z (x ) = 0 , то есть
∆x z = z (x ) − 0 = 0 и по этой	координате функция непрерывна.	Аналогично
∆ y z = z ( y ) − 0 = 0 . Отметим, что геометрически стремление в точку O (0; 0)		происходит по

координатным осям. Однако через точку O (0; 0) проходит еще множество прямых y = kx ,

на которых при x →0 y стремится к нулю одновременно. Вычислим предел функции z в этом случае.

	lim	xy	= lim	k	=	k
				1+ k 2		+ k2
	x→0 x2 + y2		x→0		1
	y→0		y→0
При	k = 0 этот предел равен нулю,		а при	k ≠ 0 предел отличен от нуля и данная
функция	разрывна в точке O (0; 0) .	Точки разрыва			функции могут образовать линии

разрыва. Например, для функции z = ln (x2 y2 ) линии разрыва образуют оси координат.

Из определения непрерывности и из свойств предела следуют свойства непрерывных функций, аналогичные соответствующим свойствам функции одной переменной.

Свойство 1.6. Сумма, разность, произведение и частное непрерывных в точке M (x; y ) функций также непрерывны в этой точке. В последнем случае

предполагается, что знаменатель отличен от нуля в точке M (x; y ) .

Свойство 1.7.	Если	функция	z = f (u, v ) непрерывна		в точке N0 (u0 ; v0 ),
функции u = u	(x, y )	и v = v (x, y ) непрерывны в точке			M 0 (x0 ; y0 ) , причем
u (x0 , y0 ) = u0	и v (x0 , y0 ) = v0 ,		то сложная функция	z	= f (u (x, y ), v (x, y ))

непрерывна в точке M 0 (x0 ; y0 ) .

Свойство 1.8. Если функция z = f (M ) непрерывна в ограниченной замкнутой

области G, то в этой области она ограничена, принимает наименьшее и наибольшее значение, а также принимает и все промежуточные значения.

Для закрепления материала решите самостоятельно следующие примеры

изадачи.

1.1.Найти область определения функции

а) z = ln (−x − y ); б) z =		+		; в)	z = arcsin	x
	y2 −1		1 − x2				; г)
						y

z= ln (x2 y2 ).

1.2.Найти область определения функции u = R2 − x2 − y2 − z2 .

1.3.	Вычислить пределы: а) lim	sin(xy)	; б)	lim	x + y	;
1.3.	Вычислить пределы: а) lim	x2 + y2	; б)	lim	− xy + y2	;
	x→0	x2 + y2		x→∞ x2	− xy + y2
в) lim (x2	y→0			y→∞
в) lim (x2	+ y2 )e−( x+ y ) .
x→∞

y→∞

117

Глава 2. Дифференциальное исчисление функций двух переменных

§2.1. Частные производные

Пусть в некоторой открытой области D плоскости XOY задана функция

двух переменных z = f ( x, y) .

Возьмем произвольную точку M 0 (x0 ; y0 ) в этой

области

образуем

частное

приращение

функции

по

∆x z(M 0 ) = f (x0 + ∆x, y0 ) − f (x0 , y0 ) . Рассмотрим теперь отношение

∆x z(M0 )

f (x0 + ∆x, y0 ) − f (x0 , y0 )

∆x

Определение 2.1. Частной производной функции z = f ( x, y)

по переменной х в

точке M 0 (x0 ; y0 )

называется предел этого отношения при

∆x → 0

(если он

существует и конечен).

z = f ( x, y) по x в точке

Для обозначения частной производной функции

M (x; y) используют символы

∂z(x, y) , z′x (x, y) ,

∂z (M ) ,

z′x (M ) .

∂x

Таким образом, ∂z

(M0 ) = lim

∆x z(M0 ) = lim

f (x0 + ∆x, y0 ) − f (x0 , y0 )

∂x

∆x→0

∆x

∆x→0

∆x

Аналогично,

считая переменную x постоянной и придавая переменной

приращение ∆y , получим частное приращение

функции

z = f ( x, y)

по

переменой y в точке M

(x ; y

) : ∆

z(M

) = f (x , y + ∆y) − f (x , y ) .

Определение 2.2. Частной производной функции z = f ( x, y)

по переменной у в

точке M 0 (x0 ; y0 )

называется предел

∂z

(M 0 ) = lim

∆y z(M 0 )

= lim

f (x , y + ∆y) − f (x , y )

∂y

∆y

∆y→0

∆y

если он существует и конечен. Другие обозначения для частной производной по у имеют вид

				∂z(x, y) ,	z′y (x, y) ,		z′y (M ) .
				∂y
Для выяснения физического смысла частных производных заметим, что
отношение		∆x z(M )	=	f (x + ∆x, y) − f (x, y)		дает среднюю скорость изменения
		∆x		∆x
					x на		отрезке MM1 , между точками
функции	z = f ( x, y)			по переменной
M (x; y )	и M1 (x + ∆x; y) . Значит, предел этого отношения при ∆x → 0 (если он

существует и конечен) характеризует мгновенную скорость изменения данной функции по аргументу x в самой точке M (x; y ) .

Аналогично, частная производная z′y (M ) характеризует скорость изменения функции z = f ( x, y) точке M (x; y ) только по аргументу y .

118

Операция

нахождения

частных

производных

f x′( x, y)

f y′(x, y)

называется дифференцированием функции

z = f ( x, y)

по

переменной

переменной y , соответственно.

по x (по y ) есть,

Фактически, частная производная функции

z = f ( x, y)

по определению, обыкновенная производная функции z ,

рассматриваемой как

функция одной переменной

(соответственно

y ) при постоянном значении

другой переменной. Поэтому, вычисление частных производных от конкретных

функций производится по известным для функции одной переменной

правилам. Только требуется помнить, по какой переменной ищется

производная, и при этом другую переменную считать постоянной.

Пример 2.1. Найти частные производные функции

f (x, y) = x2 + 5xy2 + y3 + 3x − 4 y .

Решение. Считая y постоянной,

имеем

fx′( x, y) = 2x + 5 y2 + 3 ;

считая

постоянной,

имеем f ′( x, y) = 10 xy + 3 y 2 − 4 .

Аналогично определяются и обозначаются частные производные функции

любого числа независимых переменных. Именно, частная производная от

функции u = f ( x1 , x2 ,…, xn )

по любой из независимых переменных

xi в точке

M (x1; x2 ;…; xn ) есть предел отношения частного приращения функции по

этой точке к приращению

∆xi

при

∆xi → 0

(если это предел существует и

конечен):

∂u

(M ) =

lim

∆x i u

(M ) .

∂xi

∆xi

∆x i →0

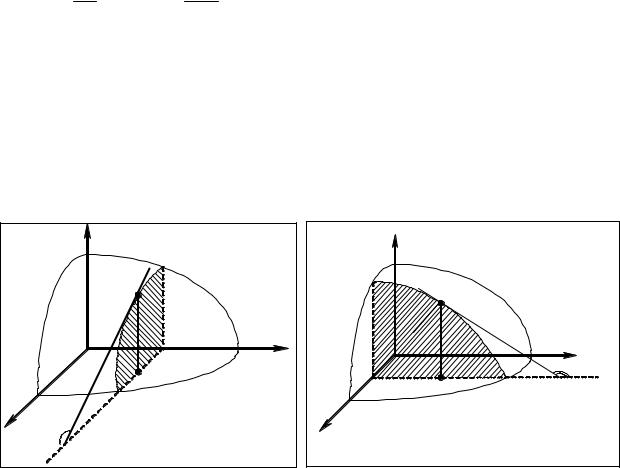
Частные производные функции двух переменных имеют простой

геометрический смысл. Предположим,

что функция z = f ( x, y)

имеет в точке

M 0 (x0 ; y0 )

частную производную по переменной x . Допустим, что поверхность

является графиком

функции z = f (x, y)

(рис.2.1).

Проведем через

точку

M 0 (x0 ; y0 )

плоскость, параллельную координатной плоскости xOz (на рисунке

заштрихована).

Уравнением

такой плоскости

будет

y = y0 . В сечении

этой

плоскости

поверхностью

получится

дуга

P0T ,

где

P0 (x0 ; y0 ; f (x0 , y0 )).

Рис.2.1

Рис.2.2

119

Построим в точке P0 касательную прямую P0 A к линии P0T . Пусть прямая P0 A образует с осью Ox угол α. Тогда fx′(M 0 ) = tg α .

Действительно, по определению, f x′(M 0 ) есть обычная производная по аргументу x от функции одной переменной f ( x, y0 ) при x = x0 . Согласно §1.2 раздела II, производная этой функции в данной точке x0 равна тангенсу угла наклона к оси Ox касательной к графику этой функции в точке x0 . Линия P0T ,

между тем, и есть график	функции f ( x, y0 ) , а прямая	P0 A – эта самая
касательная.
Аналогично, если функция z = f (x, y) имеет в точке		M 0 (x0 ; y0 ) частную
производную по переменной	y , то f y′(M0 ) = tgβ, где β –	угол наклона к оси

Oy касательной, проведенной в точке P0 к линии пересечения поверхности S и плоскости с уравнением x = x0 (на рисунке 2.2 эта плоскость заштрихована).

§2.2. Дифференциал

Пусть функция z = f (x, y ) определена в некоторой окрестности точки M (x; y ) . Составим полное приращение функции z в этой точке

∆z = f (x + ∆x, y + ∆y ) − f (x, y ) .

Функция z = f (x, y ) называется дифференцируемой в данной точке

M (x; y ) , если ее полное приращение в этой точке может быть представлено в

виде
∆z = A ∆x + B ∆y + α(∆x) ∆x + β(∆y ) ∆y ,	(2.1)
где A, B – числа, не зависящие от ∆x и ∆y , а α (∆x ) и β(∆y )	– бесконечно

малые величины при ∆x → 0 и ∆y → 0 . Первые два слагаемых выражения

(2.1) образуют главную часть приращения функции, линейную относительно

∆x и ∆y . Эта часть называется полным дифференциалом функции и

обозначается dz
dz = A ∆x + B ∆y	(2.2)

Для независимых переменных x и y приращения совпадают с дифференциалами этих переменных ∆x = dx , ∆y = dy . Учитывая это, слагаемые

выражения (2.2) называются частными дифференциалами функции				z . Таким
образом	dx z = A dx ,	dy z = B dy ,	dz = dx z + dy z .	(2.3)

Теорема 1.1	(необходимое условие дифференцируемости). Если			функция
z = f (x, y )	дифференцируема в точке M (x; y ) ,		то в этой существуют её

частные производные по переменным x и y, причем

∂∂xz = A , ∂∂yz = B .

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1612 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.09.201940.89 Кб5ДЗ Экология 1 курс.docx
#
11.04.20153.6 Mб175Диплом Баженов испр. М.Л.М..doc
#
11.04.2015213.11 Кб77диплом2.docx
#
11.04.20151.35 Mб115Дискретная_матем1.doc
#
11.04.2015836.61 Кб31Дискретная_матем2.doc
#
11.04.20152.86 Mб103ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник.pdf
#
11.04.2015183.81 Кб12ДКБ Реферат.doc
#
11.04.20153.48 Mб43ДМ Практикум.pdf
#
11.04.2015518.14 Кб29ДМ_гл1_DO.doc
#
16.09.2019501.25 Кб3ДМ_гл1_TM_чит.doc
#
11.04.2015484.86 Кб13ДМ_гл2_DO.doc