Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Телекоммуникаций и Информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник

.pdf

Скачиваний:

103

Добавлен:

11.04.2015

Размер:

2.86 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1610 11 12 13 14 15 16 > Следующая >>>

lim	f (x)	= lim	f ′(x)	,

	g(x)		g (x)

x→∞		x→∞	′

если существует предел, стоящий справа. Для доказательства последнего равенства достаточно сделать замену x = 1t , применить правило Лопиталя при t → 0 , а затем вернуться к исходной переменной.

§2.6. Виды неопределенностей и их раскрытие

Всего насчитывается семь видов неопределенностей. Рассмотрим каждый из них и покажем, как они раскрываются, т.е. как вычисляются соответствующие пределы.

Неопределённость вида		0
Неопределённость вида		0
Рассмотрим предел		0
Рассмотрим предел				f (x)
			lim	f (x)	.
			lim		.
Если lim f (x ) = lim g (x ) = 0 ,			x→a	g (x)
Если lim f (x ) = lim g (x ) = 0 ,		то при вычислении				предела отношения этих
x→a	x→a					0
функций	мы имеем неопределенность вида					0	. Выше мы подробно
функций	мы имеем неопределенность вида					0	. Выше мы подробно
						0

рассмотрели, как с помощью правила Лопиталя можно раскрывать неопределенность такого вида.

Неопределенность типа			∞
	lim f (x)= ∞		∞
Если	lim f (x)= ∞	и	lim g(x) = ∞,	то при вычислении	предела
	x→a		x→a		вида ∞ .
отношения	этих функций	мы имеем дело с		неопределенностью	вида ∞ .
					∞

Заметим, что здесь a может быть как конечным числом, так и бесконечностью. Для вычисления этих пределов справедливо то же правило Лопиталя, но в другом виде.

Теорема 2.7. Если функции f (x) и g ( x) определены и дифференцируемы на

промежутке	[a,b],	причём g ′( x) ≠ 0 и lim f (x ) = ∞ ,	lim g (x ) = ∞ , и				если
		x→a	x→a	f ′(x)
существует	предел	отношения производных, т. е.	lim	f ′(x)	= A	,	то
существует	предел	отношения производных, т. е.	lim	g′(x)	= A	,	то
			x→a	g′(x)

f (x)

существует предел lim ( ) и он также равен A.

x→a g x

∞

Доказательство. Рассмотрим неопределенность вида ∞ . Используя тождественные преобразования, имеем:

f (x )

(2.18)

lim

= lim

g (x )

x →a

x→a

g ( x) f ( x)

В правой части равенства (2.18)

получилось

неопределенность

вида

, к

которой применимо правило Лопиталя, доказанное выше.

(

)

′

lim

= lim

g (x)

x→a

x→a g(x) f (x)

x→a

g(x)

1′

= f (x)

= lim

−

g ′( x)

−

f ′( x)

= lim

g ′( x) f 2

(x)

′

x→a

g (x)

f (x)

f ( x) g (x)

Воспользовавшись тем, что предел произведения равен произведению пределов, имеем

f (x)

′

f (x)

lim

= lim

g (x)

lim

(x)

= lim

g (x)

lim

′

g(x)

g (x)

g(x)

x→a

или

f ′(x)

f (x)

lim

= lim

g (x)

x→a

g(x)

′

По условию теоремы предел в левой части последнего равенства существует и равен А, и, тем самым, теорема доказана.

Теорема остается справедливой и в том случае, когда x стремится к бесконечности.

Рассмотрим примеры.

Пример 2.4. Найти предел lim

ln x

(ε > 0).

x→∞

xε

ln x

∞

(ln x)′

Решение. lim

= lim

= 0

(xε )′

x→∞ xε

∞

x→∞

x→∞ ε xε−1

x→∞ ε xε

Отсюда, в частности, следует, что функция

g ( x) = xε

при любом положительном ε

стремится к бесконечности быстрее,

чем функция

f (x) = ln x , т. е. логарифмическая

функция возрастает медленнее, чем любая степенная функция.

Пример 2.5. Найти предел lim

xε

(ε > 0, a >1).

x→∞ ax

Решение. lim

xε

∞

= lim

(xε )′

= lim

ε xε−1

(a x )′

x→∞ a x

∞

x→∞

x→∞ ax ln a

Если ε > 0 , то справа имеем неопределенность того же типа

∞

∞ , но продолжая этот

процесс, используя

то

же

правило

Лопиталя,

в конце концов, получим степень с

отрицательным или нулевым показателем. Поэтому всегда

lim

xε

= 0 .

x→∞ ax

Таким образом, показательная функция с основанием больше единицы возрастает

быстрее степенной функции.

x 2

Пример 2.6. Найти предел

lim

2 x

x→∞

Решение. lim

∞

= lim

∞

= lim

= 0 .

∞

2x ln 2

∞

2x ln2

x→∞

Неопределенность вида 0 ∞
Если lim f (x)= 0, а lim g(x)= ∞, то при вычислении предела произведения
x→a	x→a

lim f (x)g(x) мы имеем дело с неопределенностью вида 0 ∞. Неопределенность

x→a

такого типа

легко привести либо к неопределенности вида

, либо

∞

неопределенности вида ∞ , а затем воспользоваться правилом

Лопиталя.

самом деле:

f (x )

g (x )

f (x ) g (x ) =

∞

g (x )

(x )

Пример 2.7. Найти предел:

ln x

∞

Решение. lim x ln x =

0 ∞

= lim

= − lim x = 0 .

x → 0 +

∞

x → 0 +

−

x → 0 +

x 2

Неопределённость вида ∞ − ∞

Если при вычислении предела lim( f (x)− g (x))

имеют место равенства

lim f (x) = ∞

x→a

и lim g(x) = ∞, то говорят о неопределенности вида ∞ − ∞ .

x→a

Можно произвести преобразования, сводящие это выражение к

неопределенности вида		0	или ∞ :
0				∞				1			1
	f (x )							1		−	1
			=	1	−	1	=	g (x )				f (x )	=	0	.
				1		1		g (x )				f (x )		0	.
	g (x )			1		1		1			1			0
				f (x )		g (x )			f (x )		g (x )

Иногда того же результата можно достичь значительно проще.

x −

Пример 2.8. Найти предел lim ctg

Решение.

x→0

x2 cos2 x −sin2 x

xcos x + sin x

xcos x −sin x

x −

= lim

lim ctg

sin

xsin

x→0

= lim

x cos x + sin x

lim

xcos x −sin x

= −2lim

= −

xsin2 x

sin x

x→0

+ 2cos x

Неопределенности вида 1∞,00,∞0

В случае неопределенностей вида 1∞,00,∞0 рекомендуется эти выражения сначала прологарифмировать.

Пусть y = ( f ( x))g ( x) , тогда ln y = (ln f (x)) g(x) . Предел ln y представляет неопределенность вида 0 ∞, которую мы изучили ранее. Предположим, что используя приемы, описанные выше, мы нашли lim ln y , который оказался

x→a

равный либо конечному числу A, либо +∞, либо −∞. Тогда исходный предел

будет равен, соответственно, либо e A, либо +∞, либо 0.

sin x

1−cos x

Пример 2.9. Найти предел

lim

x→0

− sin x

Решение.

Имеем

неопределенность

вида

∞

1−cos x

, тогда

1 . Пусть

y =

sin x

ln y =

. Здесь неопределенность вида 0 ∞. Найдем limln y :

− cos x

x→0

sin x

cos x

= lim

ln sin x − ln x

−

lim ln y = lim

= lim

sin x

1 − cos x

−sin x

x→0

1 − cos x

x→0

= lim

x cos x − sin x

= lim

cos x − x sin x − cos x

x→0

x sin2 x

x→0 sin2 x + 2x sin x cos x

= −lim

x sin x

= −lim

= −

sin2 x + 2x sin x

sin2 x

x→0

x→0 sin x

+ 2

x sin x

lim y = e−

Следовательно,

x→0

Для закрепления материала решите самостоятельно следующие примеры и задачи.

Найти пределы, раскрывая неопределенности, применяя правило Лопиталя:


	ln (1 + x )			x
2.1.	lim		2.2. lim(π − x)tg
		x
	x → ∞		x→π	2

2.3.	lim (cos(x)tg(5x) )
	x →π 2

2.5.lim x a r c s in x x → 0

2.7.				1
2.7.	lim x				x
	x→∞
2.9.	lim	1−cos(ax)
2.9.	lim		1− cos(bx)
	x→0		1− cos(bx)
2.11.	lim x 2 e 1 x
	x → 0
2.13.	lim			[sin(2x −1)tg(π x)]
	x→1 2
2.15.	lim	x3 −4x2 +4x
2.15.	lim
	x→2		x3 −10x +12
2.17.						x	)	1
2.17.						x		x
	lim 1+e
	x→∞(

2.4. lim ex

x→∞ x3

2.6.limx→0 (1−e2x )ctg(x)

	2.8. lim	e2 x −1
	2.8. lim	ln(1+ 2x)
	x→0	ln(1+ 2x)

			1		1
2.10.	lim		1	−	1
2.10.	lim			−	2
	x→0	x sin(x)			x
2.12.	lim	ax −bx
2.12.	lim	tg(x)
	x→0	tg(x)


2.14.	lim	e2 x − 2x −1

				x	2
	x→0
2.16.	lim		1− 2sin(x)

	x→π 6			cos( 3x)

2.18.lim (sin( x) )tg ( x )

x → 0

Глава 3. Исследование функций

§3.1. Условия возрастания и убывания функций

	Пусть	функция	y = f ( x)	задана	на промежутке от		a до	b. Введем
определения, которые будут использоваться в дальнейшем.

	y					y
	y
	f(x2)					f(x1)		b
						f(x1)	x2	b
						a x1	x2	x
						a x1		x
	f(x1)					f(x2)
				x		f(x2)
				x
	a	x1	x2	b		Рис. 3.2
		Рис. 3.1				Рис. 3.2
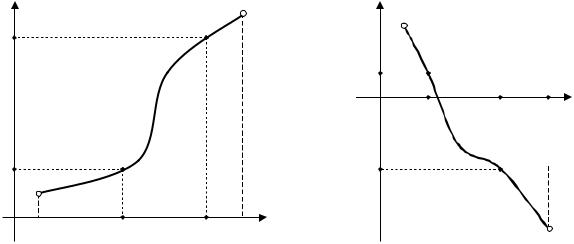
Определение 3.1. Функция y = f ( x) ,					заданная в интервале		(a,b),	называется

монотонно возрастающей, если большему значению аргумента соответствует

большее значение функции, т.е., если x1, x2 (a,b) и					x2 > x1 ,	то f (x2 ) > f (x1 )
(рис.3.1).			y = f ( x)
Определение	3.2.	Функция	y = f ( x)	называется		возрастающей
(неубывающей)	на	интервале (a,b),	если при любых		x1, x2 (a,b) таких, что

x2 > x1 , всегда выполняется неравенство f ( x2 ) ≥ f ( x1 ) .

Аналогично определяются монотонно убывающие функции и убывающие (невозрастающие) функции:

Определение 3.3. Функция y = f ( x) , заданная в интервале (a,b), называется монотонно убывающей, если большему значению аргумента соответствует

меньшее значение функции, т.е., если x1, x2 (a,b) и x2 > x1 , то f (x2 ) < f (x1 ) (рис.3.2).

Определение 3.4. Функция y = f ( x) называется убывающей (невозрастающей) на интервале (a,b), если при любых x1, x2 (a,b) , x2 > x1 , всегда выполняется

неравенство f (x2 ) ≤ f (x1 ) .

Выясним, каким образом по производной можно судить о возрастании или убывании функции в заданном промежутке. Теоремы, сформулированные и доказанные ниже, позволят с помощью производной функции найти промежутки возрастания и убывания функции.

Теорема 3.1. Если функция f (x)

определена и непрерывна на интервале (a,b),

имеет конечную производную f

′

и возрастает, то ее производная на этом

(x)

интервале не отрицательна, т.е.

f ′( x) ≥ 0 , для любого x (a,b).

Доказательство:

Пусть функция

f (x)

удовлетворяет

условиям

теоремы.

Предположим, что x произвольная точка отрезка (a,b) и

∆x > 0 произвольное

приращение,

такое,

что

x + ∆x (a,b) .

Так

как

f (x)

возрастающая,

то

f (x + ∆x) − f (x) ≥ 0 ,

и в пределе при ∆x → 0 ,

получим

′

Теорема

f (x) ≥ 0 .

доказана.

определена на интервале (a,b)

Теорема 3.2. Если функция

f (x)

и имеет на

этом интервале конечную неотрицательную производную

′

то

(x) ≥ 0 ,

функция f (x)

возрастает на интервале (a,b).

Доказательство: Пусть x1, x2

( x2 > x1 )

две произвольные точки интервала

(a,b). Применим

теорему

Лагранжа к

функции

f (x)

на отрезке

[x1,

x2],

′

− x1 ),

x1 < c < x2 . Так как

f ′(c) ≥ 0 ,

то

получим f (x2 ) − f (x1 ) = f (c) (x2

f ( x2 ) ≥ f ( x1 ) ,

т.е. функция

f (x)

возрастает

на

интервале

(a,b).

Теорема

доказана.

Совершенно аналогично доказываются нижеследующие утверждения.

Теорема 3.3. Если функция			f (x) определена		на	интервале		(a,b), имеет
конечную производную		′	и убывает, то ее производная на этом интервале
		f (x)
не положительна, т.е.		f ′( x) ≤ 0 , для любого x (a,b).
Теорема 3.4. Если функция			f (x) определена на интервале (a,b)						и имеет на
этом интервале конечную			неположительную		производную			f	′	, то
									( x) ≤ 0
функция f (x) убывает на интервале (a,b).
Замечание.	Отметим,	что функция		монотонно	возрастает		(убывает),			если
производная	функции	′		′	нет	целого	промежутка, на
		f ( x) ≥ 0 , ( f		( x) ≤ 0 ) и
′
котором f (x) тождественно равна нулю.
	§3.2. Экстремум функции. Необходимое условие

Пусть функция f (x) определена и непрерывна на отрезке [a,b]. Определение 3.5. Если функция f (x) определена и непрерывна на отрезке [a,b], то говорят, что она достигает в точке x0 (a,b)максимума (минимума), если существует окрестность точки (x0 −δ, x0 + δ) , (целиком содержащаяся в отрезке [a,b]) такая, что для всех точек x (x0 − δ, x0 + δ) этой окрестности

выполняется неравенство f (x) < f (x0 ) ( f (x) > f (x0 )) .

Определение 3.6. Точки максимума и минимума функции называются точками

экстремума функции.

Наша цель – нахождение всех значений аргумента, при которых функция достигает экстремума. В решении этой задачи основную роль играет

производная.	Первоначально предположим,	что функция f (x) в	интервале
(a,b) имеет	конечную производную. Пусть	точка x0, x0 (a,b),	, является

точкой экстремума функции. Найдем производную в этой точке. Не уменьшая общности можно предположить, что в точке x0 функция f (x) достигает

максимума. Согласно определению, найдется окрестность (x0 −δ, x0 + δ) точки

x0, для всех точек которой выполняется неравенство
Рассмотрим выражение		f (x) < f (x0 )		(3.1)
Рассмотрим выражение		f (x0 + ∆x) − f (x0 )
∆f	=	f (x0 + ∆x) − f (x0 )	,	(3.2)
∆x	=	∆x	,	(3.2)
∆x		∆x

которое при ∆x → 0 является производной функции в точке x0. Зафиксируем ∆x

таким образом, чтобы x0+∆x принадлежащему	интервалу (x0 −δ, x0 + δ) .
Величина f (x0 + ∆x) − f (x0 ) в силу соотношения	(3.1) всегда отрицательна.

Следовательно, знак выражения, определяемого равенством (3.2), полностью определяется знаком ∆x . А именно: при ∆x > 0

∆f	=	f (x0	+ ∆x) − f (x0 )	≤ 0	(3.3)
∆x			∆x

и при ∆x < 0		f (x0	+ ∆x) − f (x0 )
∆f	=			≥ 0.	(3.4)
∆x			∆x

Переходя к пределу в (3.3) и (3.4) получим выражение для производной

f ′(x0 ) . Из (3.3) вытекает, что f ′(x0 ) ≤ 0 , а из (3.4) вытекает, что f ′(x0 ) ≥ 0 .

Следовательно, f ′( x0 ) = 0 . В этом и состоит необходимое условие экстремума.

x0 x

Рис. 3.3

Экстремум будем искать только в тех точках, где производная равна нулю. На рис.3.3 это точки x0 и x1 . Особо следует отметить, что равенство нулю

производной вовсе не означает, что в этой точке функция достигает

экстремума. Это условие, подчеркнем еще раз, является необходимым, но не достаточным. Например, функция x3 имеет производную 3x2, равную нулю при x = 0 , но в этой точке функция не имеет экстремума. Эта функция везде возрастает.

Допустим теперь, что в отдельных точках интервала (a,b) функция не

имеет производных. Тогда не исключена возможность, что именно в этих точках функция может достигать минимального или максимального значения.

Например, функция x в точке x = 0 имеет минимум, хотя производной в этой

точке у этой функции не существует. Точнее, есть левая производная, равная −1, и есть правая производная, равная +1.

Суммируя все вышесказанное, сформулируем необходимое условие экстремума функции.

Теорема 3.5 (необходимое условие экстремума). Если непрерывная и дифференцируемая во всех точках некоторой окрестности точки x0 , за исключением, быть может, самой точки x0, функция y = f ( x) достигает

экстремума в точке x0 , то ее производная в точке x0 либо равна нулю, либо не существует.

Таким образом, только в точках, в которых производная равна нулю либо производная не существует, следует ожидать появления экстремума функции. Точки, в которых производная равна нулю или не существует, будем называть

критическими точками.

§3.3. Достаточные условия экстремума

Итак, если x0 - критическая точка для функции f (x) , то эта точка является

всего лишь «подозрительной» на экстремум и поведение функции в окрестности этой точки подлежит дальнейшему исследованию. Эти исследования состоят в проверке достаточных условий существования экстремума, которые будут установлены ниже.

Исследование экстремума функции с помощью первой производной

Пусть в некоторой окрестности (x0 −δ, x0 + δ) точки, (за исключением быть

может точки x0) существует конечная производная			′	так и
			f (x) и слева от x0 ,
справа от x0 сохраняет определенный знак.
Тогда возможны случаи:
′	′		′
1) f (x) > 0 при x<	x0 и f	(x) < 0 при x> x0,	т.е. производная f (x) при
переходе через точку x0	меняет знак “плюс” на “минус’’. Это означает, что в
промежутке (x0 − δ, x0 ) функция		f (x) возрастает,	а в промежутке (x0 , x0 + δ)
убывает, следовательно, значение f ( x0 ) будет наибольшим для функции				f (x)
в промежутке (x0 −δ, x0 + δ) т.е. в точке x0 функция имеет максимум.

′	′	при x > x0 , т.е. производная	′
2) f (x) < 0 при x < x0 и f (x) > 0			f (x) при
переходе через точку x0	меняет знак “минус” на “плюс’’. В этом случае легко
убедиться, что в точке x0	функция имеет минимум.
′		′	и слева и
3) f (x) > 0 как при	x < x0 так и при x > x0 либо же f (x) < 0
справа от x0 , т.е. при переходе через x0		f ′(x) не меняет знака. Тогда функция

либо все время возрастает, либо все время убывает, так что в точке x0 никакого

экстремума нет.

Итак, мы получили достаточное условие для исследования экстремума

функции.			x0 - критическая для функции
Пусть точка					f (x) . Тогда, подставляя в
производную f ′(x) сначала значения х меньшие,					чем x0 ,	а затем значения х
большие, чем x0 ,			устанавливаем знак производной вблизи от точки x0					слева и
			′	меняет знак плюс на минус, то в
справа. Если при этом производная f (x)
точке	x0	функция имеет максимум, если меняет знак минус на плюс, то в
точке x0		функция имеет минимум; если же знак производной не меняется, то
в этой точке экстремума нет.
Данное правило полностью решает вопрос в том случае, когда на
интервале		(a,b)	всего лишь конечное	число	критических		точек.	Пусть
x1 < x2	<	< xn критические точки функции f (x) . Тогда в любом промежутке
(a, x1 ),	(x1, x2 ),		…, (xn ,b) существует	производная		′	сохраняющая
						f (x) ,

постоянный знак. Рассматривая соседние промежутки и применяя достаточные условия существования экстремума функции легко определить, есть или нет экстремума в каждой из точек x1 , x2 , , xn .

Исследование экстремума функции с помощью второй производной

Пусть при первая производная функции y = f ( x) обращается в нуль, т.е. f ′( x0 ) = 0 . Такие точки будем называть стационарными точками данной функции. Допустим также, что в этой точке функция дважды

дифференцируема, т.е.	f ′′( x)	существует и		непрерывна в этой точке и в
некоторой её окрестности.
Справедливо утверждение:
Теорема 3.6: Пусть функция		f (x)	дважды непрерывно дифференцируема в
окрестности стационарной точки			x0 , если	f ′′( x0 ) > 0 ,	то функция имеет
минимум, если же f ′′( x0 ) < 0 , то - максимум.
Доказательство. Пусть выполнены условия теоремы, т.е.					f ′( x0 ) = 0 и значение
f ′′( x0 ) существует. Если	f ′′( x0 ) > 0 ,		то функция g ( x) = f ′( x) возрастает, т. е.
вблизи точки x0 слева	f ′( x) < f ′( x0 ) = 0 , а справа f ′( x) > f ′( x0 ) = 0 . Таким

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1610 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.09.201940.89 Кб5ДЗ Экология 1 курс.docx
#
11.04.20153.6 Mб175Диплом Баженов испр. М.Л.М..doc
#
11.04.2015213.11 Кб77диплом2.docx
#
11.04.20151.35 Mб115Дискретная_матем1.doc
#
11.04.2015836.61 Кб31Дискретная_матем2.doc
#
11.04.20152.86 Mб103ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник.pdf
#
11.04.2015183.81 Кб12ДКБ Реферат.doc
#
11.04.20153.48 Mб43ДМ Практикум.pdf
#
11.04.2015518.14 Кб29ДМ_гл1_DO.doc
#
16.09.2019501.25 Кб3ДМ_гл1_TM_чит.doc
#
11.04.2015484.86 Кб13ДМ_гл2_DO.doc