Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Телекоммуникаций и Информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник

.pdf

Скачиваний:

103

Добавлен:

11.04.2015

Размер:

2.86 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 167 8 9 10 11 12 13 14 15 16 > Следующая >>>

4.1.	y =		x
		x2 + x − 6
4.4.	y =		1 + x
		1 + x3

4.7.y = 1 − 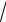x x2 −1

4.10.	y =	arcsin x
			sin 2x

4.13.	y =			2
				− 2x
	1
4.16.	y = lg (x −1)2
4.19.	y = 3x / (1−x2 )

4.2.

y =

4.3.

y =

− 3x2 − 4x

x2 −1

−

2x −1

4.5.

y =

x +1

4.6.

y =

2x2

+ 3x − 2

−

x −1

4.8.

y =

4.9.

y = (sin x)sin(1/ x)

cos x

4.11.

y =

cos(πx / 2)

4.12.

y =

sin 3x

sin 2x

x3 − x2

4.14.

y =

4.15.

y = lg(x2 + 3x)

lg x

4.17.

y = 21/ x

4.18.

y =

x −1

4.20.

y = e−1 /

4.21.

y = ln ln(1 + x2 )

Найти точки разрыва функции, установить их род, найти скачки в точках разрыва 1-го рода:

			1							1			y =				x
4.22.	y = arcsin			4.23.	y = arctg							4.24.
4.22.	y = arcsin			4.23.	y = arctg							4.24.		arctg (x )
			x						x					arctg (x )
		1				1				1				1				1 + x
4.25.	y =	1		4.26.	y =	3	x	+ 2			x	4.27.	y =			ln
	y =		1			3	x	+ 2			x
															x			1 − x
						1				1
		1+ 2x−1
						3x − 2x
						3x − 2x

Исследовать на непрерывность и построить график функции f , если:

x 2 + 1,

x ≤ 1,

x − 3,

x < 0,

4.28.

y =

2 x ,

1 < x ≤ 3,

4.29.

0 ≤ x ≤ 4,

y = x + 1,

x > 3 .

+ x ,

x > 4 .

x + 2 ,

2 x

x ≤ 0 ,

cos(x),

x ≤ 0,

4.30.

y = x ,

0 < x ≤ 1,

4.31.

y = 1− x,

0 < x ≤ 2,

2 ,

x > 1 .

x > 2.

РАЗДЕЛ II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Глава 1. Производная и дифференциал

§1.1. Определение производной

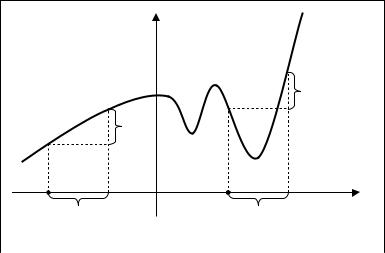
Пусть на некотором интервале (a,b) задана некоторая функция f (x) , а

задача состоит в исследовании поведения функции на этом интервале. А именно, - в выяснении того, где функция возрастает, где убывает, насколько быстро происходит это изменение, где функция достигает максимума или минимума, и т.д. Для решения всех перечисленных выше задач поступим

следующим образом. В исследуемой точке x1 (a,b) вычислим значение функции f (x1 ) , затем аргументу x1 придадим положительное приращение ∆x и вычислим значение функции f ( x1 + ∆x) . Наконец, вычислим приращение функции ∆f = f ( x1 + ∆x) − f ( x1 ) . Если ∆f положительно, то мы предполагаем, что функция возрастает справа от точки x1 ; если же ∆f отрицательно, то она

предположительно убывает справа от этой точки. Впрочем, сделанный нами вывод является спорным и, как показано на рис.1.1, сделанное заключение может оказаться как верным, так и ошибочным.

		f
		f
	x1	x2	x
	x	x
		Рис. 1.1

Из рисунка видно, что в		точке х1 приращение ∆f	положительно при

выбранном приращении ∆x и функция возрастает в окрестности этой точки. В точке х2 приращение ∆f также положительно, но функция f (x) вблизи точки

x2 убывает. Отсюда вывод: чем меньше приращение аргумента ∆x , тем

достовернее заключение о поведении функции. Все эти рассуждения приводят нас к необходимости исследовать поведение отношения приращения функции к приращению аргумента при неограниченном уменьшении приращения

аргумента, т.е. возникает потребность в исследовании величины lim ∆f .

∆x→0 ∆x

Дадим формальное определение производной. Пусть функция y = f ( x) попрежнему определена в интервале (a,b), и пусть x = x0 произвольная точка из этого интервала. Придадим аргументу приращение ∆x , такое, что x0 + ∆x не

выходит за рамки данного интервала, т.е. x0 + ∆x (a,b), при этом ∆x может иметь как положительное, так и отрицательное значение. Функция y = f ( x)

получит при этом приращение у:

∆y = ∆f (x0 ) = f (x0 + ∆x) − f (x0 )

Определение 1.1. Если предел отношения приращения функции ∆y к

вызвавшему его приращению независимого аргумента ∆x , при стремлении ∆x к нулю, существует, т.е. существует

lim	∆y	= lim	f (x0 + ∆x)	− f (x0 )	,
	∆x		∆x
∆x→0		∆x→0		y = f ( x) по независимой
то его называют производной			функции

переменной х в точке x0 и обозначают y′ = f ′( x0 ) .

Нахождение производной называется дифференцированием функции. Термин происходит от латинского «differentia» - разность, что связано с определением производной, как предела отношения соответствующих разностей значений функции и значений аргумента.

Если производная функции y = f ( x) определена в каждой точке интервала (a,b), который может быть и бесконечным интервалом, то производная сама является функцией независимой переменной х на (a,b). В этом случае можно

рассматривать две функции y = f ( x) и	y	′	′
			= f (x) . Докажем, что функция

y = f ( x) непрерывна в области дифференцирования.

Теорема 1.1 (о непрерывности дифференцируемой функции). Если функция f (x) дифференцируема в точке x (a,b), т.е. имеет в этой точке производную, то функция f (x) непрерывна в этой точке.

Доказательство. Пусть функция				f (x)		дифференцируема в точке x ,		x (a,b).
Тогда справедливо равенство					f (x0 + ∆x) − f (x0 )
lim	∆y	= lim					= f ′(x).	(1.1)
	∆x
∆x→0		∆x→0				∆x
На основании теоремы о связи предела и бесконечно малой величины и
соотношения (1.1) имеем			∆y
						′		(1.2)

			∆x = f (x) + α(∆x),
где α(∆x) - бесконечно малая величина. Из соотношения (1.2) следует, что
						′		(1.3)
		∆y = f (x) ∆x + α(∆x) .

Переходя к пределу в обеих частях соотношения (1.3) получаем:

lim ∆y = lim [ f ′( x) ∆x + α(∆x) ∆x] = f ′( x) lim ∆x + lim α(∆x) ∆x = 0

∆x→ 0	∆x→ 0	∆x→ 0	∆x→ 0
		,
т.е., lim ∆y = 0 , или		lim f (x + ∆x) = f (x) , а это означает,	что функция f (x) в
∆x→0		∆x→0
точке x ,	x (a, b) есть непрерывная функция.

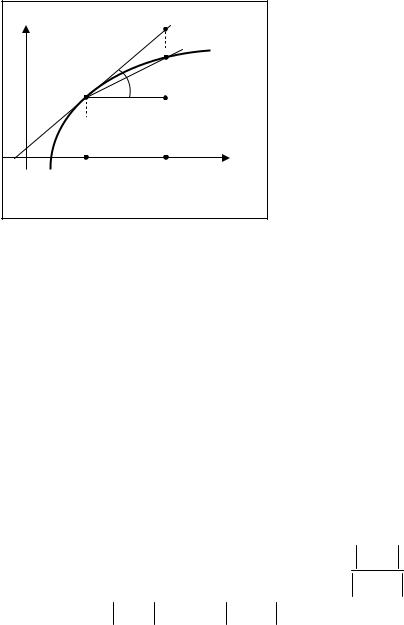
§1.2. Геометрический смысл производной.

Уравнение касательной

Покажем, что производная функции

y = f ( x)

имеет

простой

геометрический смысл, тесно связанный с уравнением касательной к графику

функции. Прежде

всего,

дадим

определение

касательной

линии в

точке

M0 (x0 ; f (x0 )).

Пусть задана плоскость с декартовой

системой

координат,

пусть

функция

y = f ( x)

определяет некоторую линию L в

М0

М1

этой плоскости (рис.1.2). Касательная к

линии

точке

M 0 ,

определяется

следующим образом. На линии L возьмем

x0 +∆x

точку

соответствующую

значению

Рис.1.2

функции в точке x0 + ∆x . Через точки M 0 и

M проведем секущую M 0 M . Касательной к

L назовем

линии

прямую

M 0 K , к которой стремится секущая

M 0 M

при

∆x → 0 . Будем считать, что такая предельная прямая существует. В этом случае

хорда M 0 M стремится к нулю, угол KM 0 M также стремится к нулю.

Учитывая все вышесказанное, можно сформулировать предложение,

которое и определяет геометрический смысл производной.

Теорема 1.2. Если функция

y = f ( x) дифференцируема в точке M0 (x0 ; f (x0 )),

то касательная, проведенная к графику функции y = f ( x)

в точке M 0 , имеет

угловой коэффициент, равный значению производной функции в этой точке,

т.е. k = f ′( x0 )

Доказательство. Пусть M 0 K -

касательная к линии,

определяемой

графиком функции y = f ( x) , в точке M 0 ( x0 , f ( x0 )) . Обозначим угол M 1M 0 K

через α; тогда угловой коэффициент прямой

M 0 K равен

tg α . Рассмотрим

секущую M 0 M , её угловой коэффициент вычисляется следующим образом:

tg ( M1M0M )

MM1

(1.4)

M0M1

Так как

MM1 = ∆x , а

M0M1

= ∆y то равенство (1.4) можно переписать в

виде

M ) = ∆y

tg( M M

(1.5)

∆x

В обеих частях равенства (1.5) перейдем к пределу при ∆x → 0 . Согласно

определению касательной и производной, имеем

lim tg ( M1M 0 M ) = tg α ,

∆x→0

∆y

lim

= f ′(x0 ) .

∆x→0

∆x

Отсюда и равенства (1.5) вытекает, что tg α = f ′( x0 ) . Теорема доказана. Замечание. Используя только что доказанную теорему, легко выписать

уравнение касательной линии	к графику	функции	y = f ( x) в	точке
M 0 ( x0 , f ( x0 )) . Воспользовавшись	уравнением	прямой,	проходящей	через
заданную точку с заданным угловым коэффициентом наклона, имеем:
y − f ( x0 ) = f ′( x0 ) ( x − x0 )				(1.6)

Полученное уравнение прямой (1.6) является уравнением касательной к линии графика функции y = f ( x) в точке M 0 ( x0 , f ( x0 )) .

§1.3. Правила дифференцирования

Для дифференцирования функций необходимо знать правила дифференцирования и формулы дифференцирования основных элементарных функций. Цель настоящего параграфа – вывод основных правил дифференцирования.

Предложение 1.1. Производная постоянной величины равна нулю, т.е. (c)′ = 0 .

Доказательство. Пусть y = c , тогда при любом x , функция y = y ( x) = c .

Отсюда ∆y = y(x + ∆x) − y(x) = c − c = 0		, т.е.	∆y	= 0	при любом ∆x , и тогда
Отсюда ∆y = y(x + ∆x) − y(x) = c − c = 0		, т.е.	∆x	= 0	при любом ∆x , и тогда
	∆y		∆x
y′ = lim	∆y	= 0 .
∆x→0	∆x

Предложение 1.2. Производная функции y = x равна единице, т.е. (x)′ =1.

Доказательство. Пусть y = x , тогда ∆y = y(x + ∆x) − y(x) = x + ∆x − x = ∆x . Следовательно, при любом значении величины ∆x всегда имеет место

равенство ∆y		=1, поэтому y′ = lim	∆y =1.
∆x		∆x→0	∆x
Предложение 1.3. Производная			суммы	(разности) функций равна сумме
(разности) их производных, т.е.			(u + v)′ = u′ + v′
			(u + v)′ = u′ + v′
			′	= u	′	′
			(u − v)	= u		− v
Эти равенства справедливы только тогда, когда существуют производные
слагаемых u	′	′
слагаемых u		и v .

Доказательство. Рассмотрим случай, когда y = u + v . В этом случае имеем:

∆y = y(x + ∆x) − y(x) = u(x + ∆x) + v(x + ∆x) − u(x) − v(x) =

= (u(x + ∆x) − u(x))+ (v(x + ∆x) − v(x)) = ∆u + ∆v.

Отсюда, используя утверждение, что предел суммы равен сумме пределов,

получаем:	∆y		∆u + ∆v			∆u		∆v
y′ = lim	∆y	= lim	∆u + ∆v	= lim		∆u	+ lim	∆v	= u′ + v′.
∆x→0	∆x	∆x→0	∆x		∆x→0	∆x	∆x→0	∆x
			′	′	′
Справедливость равенства (u − v) = u					− v доказывается аналогично.

Предложение 1.4. Производная произведения равна сумме произведений производной первого сомножителя на второй и производной второго сомножителя на первый, т.е., если y = u v , то y′ = u′ v + u v′ .

Доказательство. Если y = u v , то имеем

∆y = y(x + ∆x) − y(x) = u(x + ∆x) v(x + ∆x) − u(x) v(x) .

(1.7)

К правой

части

равенства (1.7)

прибавим и

вычтем

произведение

u(x) v(x + ∆x) и тогда, группируя, получим

∆y = (u(x + ∆x) v(x + ∆x) −u(x) v(x + ∆x)) + (u(x) v(x + ∆x) −u(x) v(x)) =

= v(x + ∆x) (u(x + ∆x) −u(x)) + u(x) (v(x + ∆x) − v(x)).

Так как

u(x + ∆x) − u(x) = ∆u и v(x + ∆x) − v(x) = ∆v ,

то последнее неравенство перепишется в виде

∆y = v(x + ∆x) ∆u + u(x) ∆v .

Разделим обе части последнего равенства на ∆x . Затем, переходя к пределу

и учитывая, что предел суммы равен сумме пределов, получаем

y′ = lim

∆y

= lim

v ( x + ∆x) ∆u + u ( x ) ∆v

= lim v( x + ∆x ) lim

∆u + u ( x ) lim

∆v

∆x

∆x → 0

∆x

∆x → 0

∆x

∆x → 0

В наших обозначениях:

∆u = u′(x) = u′; lim

∆v

u(x) = u ;

lim v(x + ∆x) = v(x) = v ;

lim

= v′(x) = v′.

∆x→0

∆x

∆x→0

∆x

Следовательно,

(u v )′ = u′ v + u v′ . Предложение доказано.

Приведем несколько следствий из доказанного утверждения.

Следствие 1.4.1. Постоянный множитель можно выносить за знак производной, т.е. (c u )′ = c u′ .

В	самом		деле, согласно			предложению 1.4, имеет место равенство
′	′			′		′
(c u )		u + c u			. Но так как		= 0, из последнего соотношения вытекает
	= c					c

доказываемое предложение.

Следствие 1.4.2. Дифференцирование трех и более сомножителей.


Рассмотрим случай, когда		y = u v w . Представим эту функцию в виде
y = (u v) w . Тогда, используя		правило	дифференцирования	произведения,
имеем:	y′ = (u v )′ w + (u v ) w′. Но		(u v )′ = u′ v + u v′ .	Отсюда и из

предыдущего равенства получаем

y′ = u′ v w + u v′ w + u v w′.

Совершенно аналогично доказывается справедливость равенства:

(u v w t )′ = u′ v w t + u v′ w t + u v w′ t + u v w t′.

Окончательно правило дифференцирования трех и более сомножителей можно сформулировать так: производную первого сомножителя умножаем на произведение всех остальных функций, затем производную второго

сомножителя умножаем на произведение всех остальных сомножителей и этот процесс продолжаем до последнего сомножителя; полученные произведения нужно сложить.

Предложение 1.5. Производная дроби является дробью, числитель которой равен разности произведения производной числителя на знаменатель и произведения числителя на производную знаменателя, а знаменатель равен квадрату знаменателя исходной дроби, т.е.

	′		′		′
u		=	u v − uv			.

				v	2
v				v

Доказательство. Пусть y = uv , тогда приращение функции будет таково:

	∆y =	u(x + ∆x)	−	u(x)	=	u(x + ∆x) v(x) − u(x) v(x + ∆x)	=
	∆y =	v(x + ∆x)	−	v(x)	=	v(x + ∆x) v(x)	=
		v(x + ∆x)		v(x)		v(x + ∆x) v(x)
=	(u(x + ∆x) v(x) − u(x) v(x)) − (u(x) v(x + ∆x) − u(x) v(x))							,
					v(x + ∆x) v(x)
или окончательно: ∆y = ∆u v(x) − u(x) ∆v .
		v(x + ∆x) v(x)
Разделив	обе части последнего равенства на и используя							свойства
пределов, имеем:

y′ = lim ∆y =

∆x→0 ∆x

Так как lim v(x + ∆x) = v(x) = v ,	lim
∆x→0	∆x→0

Предложение доказано.

v(x) lim			∆u	−u(x) lim			∆v
		∆x→0	∆x			∆x→0	∆x	.
	v(x) lim v(x + ∆x)							.
	v(x) lim v(x + ∆x)
			∆x→0
∆u	= u′, lim			∆v		= v′, то получаем
∆x		∆x→0		∆x
		′		′
y′	=	u v − uv			.
y′	=	v2			.
		v2

§1.4. Производные элементарных функций

Производная степенной функции	y = xa вычисляется по
Предложение 1.6. Производная степенной функции	y = xa вычисляется по
формуле y′ = a xa−1 .
Доказательство. Пусть y = xa , тогда приращение ∆y	функции можно записать
в виде

∆y = (x + ∆x )	a	− x	a	= x	a		∆x a
						1 +
						1 +

							x

−1 .

Рассмотрим теперь отношение приращения функции к приращению аргумента

		x	a		∆x a
				1 +		− 1
				1 +		− 1
∆y
∆y	=				x
∆x	=			∆x

Так как lim ∆x = 0 ; для любого x ≠ 0 , то величина

∆x→0 x

(1.8)

∆x – бесконечно малая x

при	∆x → 0 . Следовательно, величина		+	∆x a
при	∆x → 0 . Следовательно, величина	1	+		, согласно известной
				x

эквивалентности ( раздел I §3.9), эквивалентна величине 1+ a ∆xx .

Отсюда и из теоремы о вычислении пределов с помощью эквивалентных величин из (1.8) получаем:

1 +

∆x

−1

+ a

∆y

−1

y′ = lim

= lim

∆x

∆x→0

= lim a

xa ∆x

= a xa−1 .

Частные случаи:

∆x→0

x ∆x

1. Для y = x2

производная y′ = (x2 )′ = 2 x2−1 = 2x .

′

−1

−

2. Для y = x производная

y′

= x 2

x 2

′

−1

−

3. Для y = 3 x производная

y′

= x 3

x 3

4. Для	y =	1	производная y′ = (x−1 )′ = −x−1−1 = −x−2 = −				1	.
4. Для	y =		производная y′ = (x−1 )′ = −x−1−1 = −x−2 = −				2	.
		x					x
Производная синуса и косинуса
Предложение 1.7. Производные функций y = sin x						и y = cos x вычисляются по
формулам:			(sin x)′ = cos x
			(sin x)′ = cos x				(1.9)
			(cos x)′ = −sin x				(1.9)
			(cos x)′ = −sin x
Доказательство. Установим справедливость первого равенства из (1.9).
Если	y = sin x , то ∆y = sin( x + ∆x) − sin x . Воспользовавшись формулой
разности синусов, имеем:				∆x		∆x
			∆y = 2 sin	∆x		∆x
			∆y = 2 sin	2	cos x +	.
				2		2

Так как ∆x → 0 , то величина sin

∆x

эквивалентна величине

∆x

и, тогда:

∆x

sin

∆y

cos x +

∆x cos x +

y′ = lim

= 2 lim

= cos x

∆x

2 ∆x

∆x→0

Тем самым первая формула из (1.9) доказана. Установим справедливость второй из формул (1.9). Если y = cos x , то ∆y = cos( x + ∆x) − cos x . Используя

формулу разности косинуса, имеем:

∆y = cos( x + ∆x) − cos x = −2 sin

∆x

sin x +

Отсюда и из эквивалентности sin ∆x величине

∆x

, при ∆x → 0 получаем

∆x

′

∆y

∆x sin x +

= (cos x) = lim

= −2

lim

= −sin x .

∆x

2 ∆x

∆x→0

Предложение полностью доказано.

Производные тангенса и котангенса

Предложение 1.8. Производные функций

y = tg x

y = ctg x

вычисляются по

формулам:

(tg x)′ =

(ctg x)′ = −

cos2 x

sin2 x

Доказательство. Для вычисления производных этих функций воспользуемся правилом вычисления производной от частного и формулами производных для функций sin x и cos x . Тогда

sin x ′

cos x (sin x)′ − sin x (cos x)′

cos2

x + sin2 x

(tg x)′ =

cos

cos x

Аналогично,

cos x ′

(cos x )′ sin x − (sin x)′ cos x

−sin2 x − cos2 x

(ctg x)′ =

= −

sin

cos

sin

sin x

Производная показательной функции

Предложение

1.9. Производная функции

y = ax

находится

по

формуле

(ax )′ = ax ln a ,

a > 0, a ≠ 1. В частности, (ex )′ = ex .

Доказательство. Пусть y = ax , тогда

∆y = ax+∆x − ax = ax a∆x − ax = ax (a∆x −1) = ax (e∆x ln a −1).

(1.10)

e∆x ln a −1

Но величина эквивалентна ∆x ln a при ∆x → 0 . Таким образом, из

(1.10) имеем

y′ =	(	ax	′ = lim		∆y	= lim	ax (e∆x ln a −1)	= lim	ax ∆x ln a	= ax ln a .
					∆x		∆x		∆x
			)	∆x→0		∆x→0		∆x→0

Если a = e , то из доказанного равенства вытекает, что (ex )′ = ex .

Производная логарифмической функции

Предложение 1.10. Производная функции y = ln x вычисляется по формуле

(ln x)′ = 1x .

Доказательство. Пусть y = ln x , тогда приращение функции будет иметь вид

	+	∆x	,
∆y = ln(x + ∆x) − ln x = ln 1	+		,
		x

∆x

при ∆x → 0 . Отсюда и из

но величина ln 1+

эквивалентна

предыдущего равенства имеем

∆x

∆y

1 +

∆x

y′ = lim

= lim

∆x

∆x→0

∆x→0 x∆x x

Предложение доказано.

Следствие. Если y = loga x , где a > 0, a ≠ 1, то (loga x)′ =

ln a

ln x

′

В самом деле

y′ = (loga x )′ =

. Здесь использована формула

ln a

перехода к другому основанию логарифма

loga x = logb x , logb a

и правило дифференцирования, согласно которому постоянный множитель можно выносить за знак производной.

Производная сложной функции
Рассмотрим сложную функцию	y = f (u) , где	u = u(x) является в свою
очередь функцией независимой	переменной	х. Например, функция

y = sin(x2 + 4) является сложной функцией, здесь u = x2 + 4 . Производные таких

функций будем находить, используя следующее утверждение.

Предложение 1.11. Производная сложной функции по независимой переменной равна её производной по промежуточной переменной, умноженной на производную промежуточной переменной по переменной независимой, т.е. если

y = f (u) , где u = u(x) , то y 'x = f 'u (u) u 'x .

Доказательство. Зафиксируем независимую переменную х, тогда функции u и f будут иметь, соответственно, значения u(x) и f (u) . Придадим независимой

переменной приращение ∆x . Тогда, по определению производной,

<<< < Предыдущая 1 2 3 4 5 67 / 167 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.09.201940.89 Кб5ДЗ Экология 1 курс.docx
#
11.04.20153.6 Mб175Диплом Баженов испр. М.Л.М..doc
#
11.04.2015213.11 Кб77диплом2.docx
#
11.04.20151.35 Mб115Дискретная_матем1.doc
#
11.04.2015836.61 Кб31Дискретная_матем2.doc
#
11.04.20152.86 Mб103ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник.pdf
#
11.04.2015183.81 Кб12ДКБ Реферат.doc
#
11.04.20153.48 Mб43ДМ Практикум.pdf
#
11.04.2015518.14 Кб29ДМ_гл1_DO.doc
#
16.09.2019501.25 Кб3ДМ_гл1_TM_чит.doc
#
11.04.2015484.86 Кб13ДМ_гл2_DO.doc