
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник
.pdf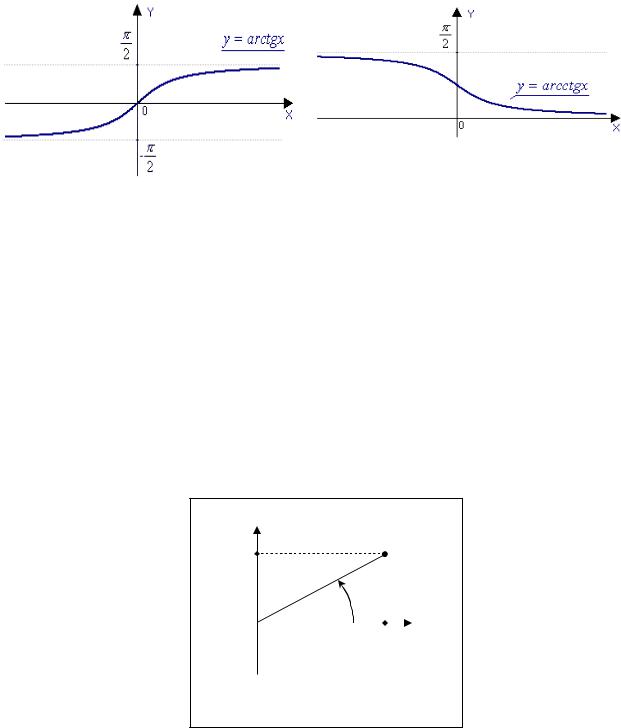
определения всю числовую ось, а областью значений – интервал |
|
− |
π |
, |
π |
|
2 |
. |
|||
|
|
|
|
2 |
График функции y = arctg x изображен на рисунке 2.22.
Функция y = arcctg x , по определению, есть дуга в интервале (0, π), котангенс которой равен x, т.е. справедливо равенство ctg y = x .
|
|
Рис. 2.22 |
|
Рис. 2.23 |
|
|
|
|
|
|
|
|
|
Решая |
это |
уравнение |
относительно |
y , |
получаем: |
|
y = Arcctg x = arcctg x + kπ, k = 0, ±1, ±2,...
График функции y = arcctg x изображен на рисунке 2.23.
§2.5. Задание функции в полярных координатах
При заданной декартовой системе координат положение точки на плоскости определяется с помощью двух чисел, а именно, значениями абсциссы и ординаты. Однако, кроме декартовой, можно использовать и другие системы координат. Напомним, что вместо декартова ортонормированного базиса на плоскости, можно в качестве базиса выбрать любые два неколлинеарных вектора. Такие системы существуют, но их постоянное употребление слишком громоздко и требует больших вычислений по сравнению с используемой нами декартовой системой координат.
|
y |
|
М |
|
r |
|
φ |
O |
х |
А |
Рис. 2.24
Однако, другая, так называемая полярная система координат, получила достаточно широкое распространение. Опишем эту систему подробнее. Полярная система координат вводится следующим образом:
31
-на плоскости фиксируется некоторая точка О, называемая в дальнейшем
полюсом;
-из полюса О проводим направленную прямую Ox , которую назовем
полярной осью.
Положение произвольной точки М на плоскости относительно выбранной системы координат определим двумя числами (рис.2.24). Первое число – длина отрезка OM = r . Это число назовём полярным радиусом точки М. Второе число
–угол ϕ = MOX , между полярной осью и полярным радиусом точки М. Это
число назовём полярным углом. Как обычно, угол считаем положительным, если отсчет ведется против часовой стрелки. Пара чисел r и ϕ составляют полярные координаты точки М. Как и в декартовой системе координат, в этом случае, используется запись M (r,ϕ) . Очевидно, что полярный радиус r может изменяться от 0 до +∞; полярный угол ϕ меняется в пределах от −π до π (или от 0 до 2π). Для полюса О полярный радиус равен нулю, а полярный угол не определен. При решении конкретных задач могут рассматриваться и другие значения углов, т.е. углы, не входящие в указанный интервал.
Рассмотрим взаимосвязь между декартовыми и полярными координатами. Для этого зафиксируем декартов базис и введём полярную систему координат, у которой полюс совпадает с началом координат декартовой системы и
полярная ось совпадает с положительной полуосью Ox . |
|
Для произвольной точки M (x, y) , тогда имеем OA = x ; |
AM = y ; OM = r и |
MOA = ϕ (рис.2.24). Считая ϕ острым углом в прямоугольном треугольнике |
|
AOM , получим |
|
OA = OM cos ϕ; AM = OM sin ϕ |
|
или |
|
x = r cosϕ, y = r sin ϕ. |
(2.3) |
Полученные формулы справедливы при любом 0 ≤ ϕ ≤ 2π . Эти формулы и выражают взаимосвязь между декартовыми и полярными координатами. Из
|
|
|
|
|
|
|
AM |
|
|
этого же прямоугольника видно, что OM = OA2 + AM 2 , tgϕ = |
, т.е. |
||||||||
OA |
|||||||||
r = |
|
, tg ϕ = |
y |
. |
|
|
|||
x2 + y2 |
|
(2.4) |
|||||||
|
|
||||||||
|
|
|
|
x |
|
|
|||
Формула (2.4) выражает полярные координаты точки через декартовы координаты этой же точки. Отметим, что для вычисления угла ϕ по формуле (2.4) нужна дополнительная информация, например, в каком квадранте находится точка M (сравните с формулами (1.11) нахождения аргумента комплексного числа).
Полярные координаты интересны тем, что многие кривые, имеющие в декартовой системе уравнений достаточно сложный вид, в полярной системе имеют значительно более простой вид.
Приведем три примера
32
1. Уравнение окружности с центром в начале координат и радиусом R в декартовой системе координат определяется уравнением x2 + y2 = R2 .
В полярной системе координат та же самая окружность определяется уравнением r = R .
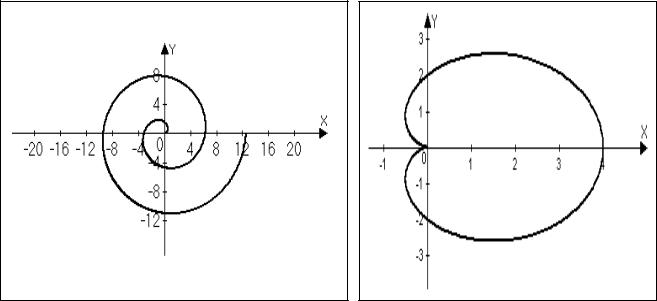
2. Достаточно простое уравнение r = ϕ, являющееся линейным относительно ϕ , определяет сложную кривую, изображенную на рис.2.25 и
называемую спиралью Архимеда.
3. Уравнение кардиоиды в декартовых координатах имеет вид
(x2 + y2 )(x2 + y2 − 2ax) − a2 y2 = 0, a > 0 .
В полярных координатах уравнение принимает значительно более простой вид: r = a(1+ cosϕ) .
График функции при a = 2 приведен на рис. 2.26.
Рис. 2.26
Рис. 2.25
33
§2.6. Уравнение кривой в параметрическом виде
Рассмотрим некоторую кривую на плоскости, уравнение которой определяется равенством F (x, y) = 0 и связывает декартовы координаты точки
x и y. Достаточно часто вместо уравнения F (x, y) = 0 даются выражения
текущих координат x и y в виде функций от некоторой переменной величины t , т.е. x = ϕ(t) , y = ψ(t) . Величину t при этом называют параметром.
Например, параметрическое уравнение окружности радиуса R с центром в начале координат имеет вид
x = R cost , y = R sin t .
Чтобы получить уравнение функции (в неявном виде), нужно исключить параметр t. Для этого возведём обе части равенств в квадрат и, сложив, получим
x2 + y2 = R2 (cos2 t + sin2 t) = R2 .
Другой пример: параметрическое уравнение линии имеет вид: x = a cos t, y = b sin t .
Эту линию можно приблизительно построить по точкам, придавая различные значения t , и нанося точки с соответствующими координатами (x; y) на
координатную плоскость. Соединяя их линией, получим кривую – эллипс, неявное уравнение которого можно получить аналогично предыдущему примеру:
x2 + y2 =1 a2 b2
Еще пример. Пусть линия задана параметрическими уравнениями
|
a |
|
1 |
|
b |
1 |
|
|||
x = |
|
t + |
|
|
, y = |
|
t − |
|
|
, |
2 |
|
|
|
|||||||
|
|
t |
|
2 |
t |
|
||||
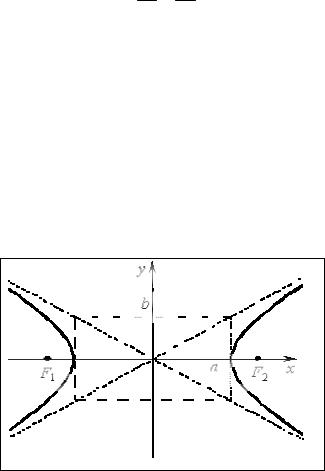
Её уравнение в декартовой системе координат – это каноническое уравнение
гиперболы: |
x2 |
− |
|
y2 |
=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В самом деле, |
x2 |
|
− |
y2 |
= |
1 |
|
|
t + |
1 2 |
− |
|
t − |
1 2 |
= |
1 |
t |
2 |
+ 2 |
+ |
1 |
− t |
2 |
+ 2 |
− |
1 |
=1. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
2 |
|||||||||||||||||||||||
|
|
a |
|
|
b |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
t |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
t |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
График этой кривой приведен на рис.2.27.
Рис.2.27
34
Для закрепления материала решите самостоятельно следующие примеры и задачи.
|
1 |
|
|
1 |
|
f (x) = |
1+ x |
|
||
2.1. Найти f (0), f (−x), f (x +1), f (x) +1, f |
|
|
, |
|
, если |
|
|
|
. |
|
|
f (x) |
1 |
− x |
|||||||
x |
|
|
|
|
||||||
2.2. Найти область определения и множество значений каждой из функций:
а) |
y = ln(x − 2) , б) |
y = |
|
|
1 |
|
, в) y = ex−1 , г) y = arcsin |
1 − x |
. |
|
|
|
|
|
|
|
||||||||||
|
x2 − 4 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
2.3. Исследовать функции на четность и нечетность |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
f (x) = |
ex |
−1 |
, в) f (x) = x2 − 3x3 , г) |
|
|
|
|
|
|
|
||||||||||||
а) |
f (x) = sin x − cos x , б) |
f (x) = x2 +1 . |
||||||||||||||||||||||||
ex |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|||
2.4. Исследовать функции на периодичность |
|
|
|
|
|
|
|
|||||||||||||||||||
а) |
f (x) = sin2 x , б) |
f (x) = sin (x2 ), в) |
f (x) = cos x − cos 2x − cos 4x . |
|||||||||||||||||||||||
2.5. Установить, какие из функций имеют обратные, найти |
||||||||||||||||||||||||||
соответствующие обратные функции и их области определения |
|
|
|
|
|
|
|
|||||||||||||||||||
а) |
y = 2x − 3 , б) y = 3x2 , в) |
y = ex |
−1, г) y = cos 2x . |
|
|
|
|
|
|
|
||||||||||||||||
2.6. Установить, композицией каких основных элементарных функций |
||||||||||||||||||||||||||
являются следующие сложные функции: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
y = ln cos2 x , б) |
y = |
|
|
1 |
|
|
|
|
|
|
= lg (arctg (2tg x )), г) y = |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
а) |
|
|
|
|
|
, в) y |
|
arcsin 3 x . |
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
sin ( |
x3 ) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.7. Построить графики функций, заданных в полярной системе координат: |
||||||||||||||||||||||||||
а) |
r = |
1 |
, б) |
r = sin ϕ , в) |
r = cos2 ϕ . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.8. Построить графики функций, заданных параметрически: |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = t −1 |
x = t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а) |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
, б) |
= t3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
y = t +1 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35
|
|
|
|
|
Глава 3. Теория пределов |
|
|
|
|
|
|||||
|
|
|
|
|
§3.1. Предел функции |
|
|
|
|
|
|||||
|
В этой главе вводится одно из важнейших понятий в математике – понятие |
||||||||||||||
предела функции в точке. Теория пределов образует основание |
|||||||||||||||
математического анализа. Отметим, что при изучении поведения функции |
|||||||||||||||
понятие предела играет фундаментальную роль. |
|
|
|
|
|
|
|||||||||
|
Пусть независимая переменная |
x приближается к числу x0 , |
т.е. величине |
||||||||||||
x придаются значения, сколь угодно близкие |
x0 , но не равные |
x0 , Если при |
|||||||||||||
этом соответствующие значения функции f (x) |
приближаются к числу A , |
то |
|||||||||||||
число A называется пределом функции f (x) при x , стремящемся к x0 . Такое |
|||||||||||||||
определение может быть достаточно понятное, но недостаточно точное. Дадим |
|||||||||||||||
более строгое определение предела функции. |
|
|
|
|
|
|
x , |
||||||||
Определение 3.1. |
Число |
A |
называют пределом функции |
f (x) |
при |
||||||||||
стремящемся к x0 , если для любого, |
сколь угодно малого числа ε , существует |
||||||||||||||
положительное число |
δ такое, что для всех значений x , удовлетворяющих |
||||||||||||||
неравенству 0 < x − x0 |
< δ, выполняется неравенство f (x) − A < ε . |
|
|
||||||||||||
|
|
|
|
|
|
|
lim f (x) = A |
. |
|
|
|
|
|
|
|
|
Этот факт записывают так: x→x |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Символ « lim » означает «предел», а |
x0 называют предельной точкой. Особо |
||||||||||||||
следует отметить, что при вычислении предела функции требуется, чтобы |
|||||||||||||||
функция была определена в некоторой окрестности точки x0 , |
и не требуется, |
||||||||||||||
чтобы она была определена в самой точке x0 . |
|
y |
|
|
|
|
|
||||||||
Например, функция |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
f (x) = x − 2 |
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x − 2 |
x0 = 2 , |
|
|
|
|
|
|
|
|
|
не |
определена |
в |
точке |
однако |
|
|
|
2 |
|
x |
|
||||
совершенно очевидно, что |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
lim x − 2 =1. |
|
|
|
Рис. 3.1 |
|
|
|
|||||
|
|
|
x→2 |
x − 2 |
|
|
|
|
|
|
|
|
|
|
|
График этой функции имеет вид, представленный на рис.3.1. |
|
|
|
|
|
||||||||||
|
Непосредственно из определения предела вытекает, что если функция при |
||||||||||||||
x → x0 , имеет предел, то этот предел единственный. В самом деле, допустим, |
|||||||||||||||
что |
lim f (x) = A и |
lim f (x) = B . Тогда для любого значения |
ε |
существуют |
|||||||||||
|
x→x0 |
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
значения δ1 |
и δ2 такие, что, |
если выполнится неравенство |
0 < x − x0 |
<δ1 , |
то |
||||||||||
f (x) − A < ε, |
и |
если выполнится неравенство |
0 < x − x0 <δ2 , |
то |
f (x) − B < ε . |
||||||||||
Возьмём δ = min(δ1,δ2 ) , и тогда при выполнении неравенства |
0 < x − x0 < δ, |
||||||||||||||
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|

выполняются |
одновременно |
неравенства |
y |
|
|
|
|
||||||||
f (x) − A < ε |
и |
f (x) − B <ε. |
В таком случае |
|
|
|
|
||||||||
|
|
|
|
|
|||||||||||
разность |
A − B |
может быть |
представлена |
A+ε |
|
|
|
|
|||||||
так: A− B = (A− f (x))+(f (x) − B) . Используя |
А |
|
|
В |
|
||||||||||
|
|
|
|
|
a +b ≤ a + b , |
|
|
|
|
|
|
||||
свойство |
модуля |
|
имеем |
A−ε |
|
|
|
|
|||||||
A − B ≤ f (x) − A + f (x) − B ≤ 2ε . |
Так как |
|
ε |
|
|
|
|
||||||||
|
|
|
|
|
x |
||||||||||
можно выбрать сколь угодно малым, то из |
|
|
|
|
|||||||||||
|
|
x0 − δ |
x |
x0 + δ |
|||||||||||
последнего |
соотношения |
вытекает, |
что |
|
|
||||||||||
A − B = 0 , т.е. A = B . |
|
|
|
|
|
|
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
Рис. 3.2 |
|
|
|||||
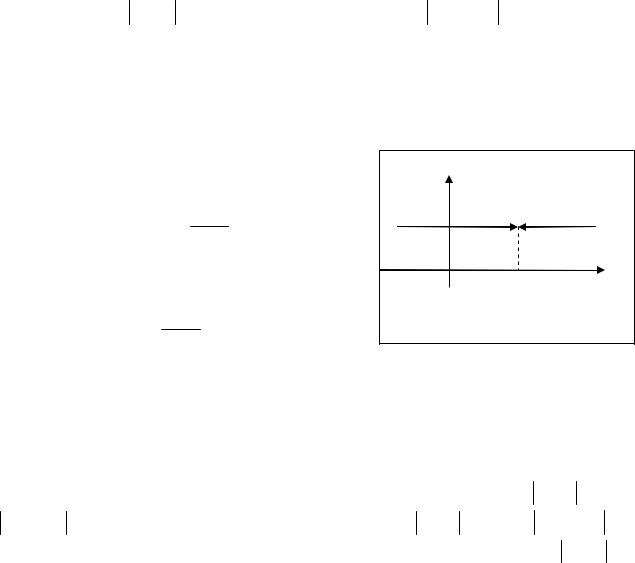
Геометрическую |
|
интерпретацию |
|
|
|
|
|||||||||
|
|
x0 |
|
|
|
||||||||||
предела |
поясним, |
используя |
рисунок |
3.2. |
Через |
проведем |
прямую |
||||||||
параллельную оси |
OY до пересечения с графиком функции в точке B . Из |
||||||||||||||
точки B проведем прямую параллельную |
оси OX до пересечения с осью OY |
||||||||||||||
в точке |
A . Выберем произвольное число |
ε>0. Тогда найдется число δ > 0 |
|||||||||||||
такое, |
что |
|
часть |
графика |
функции, |
соответствующая |
окрестности |
||||||||
x (x0 − δ, x0 + δ), |
будет содержаться |
в |
полосе между |
прямыми, уравнения |
|||||||||||
которых |
y = A − ε и |
y = A + ε . Если неограниченно уменьшать величину ε |
|||||||||||||
(сужать полосу), то уменьшается и величина δ. Легко видеть, что для всякого |
|||||||||||||||
положительного и сколь угодно малого значения ε найдется соответствующее |
|||||||||||||||
значение δ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим также, что если функция постоянна в окрестности точки x = x0 , |
|||||||||||||||
т.е. f ( x) = C , то lim f (x) = lim C = C . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
x→x0 |
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
Рассмотрим пример функции, не имеющей предела в данной точке. Пусть |
|||||||||||||||
f (x) = |
x , при x ≠ 0 |
. В точке x = 0 функция не определена, |
при этом для всех |
||||||||||||||
x > 0 , |
x |
|
f ( x) = 1, |
|
|
|
x < 0 |
|
|
|
f ( x) = −1 . Поэтому не |
||||||
очевидно, |
а для всех |
имеем |
|||||||||||||||
|
|
y |
|
|
|
существует |
|
числа, |
к которому |
значения |
|||||||
|
|
|
|
|
функции f (x) были бы близки для всех x |
||||||||||||
|
|
1 |
|
|
|
||||||||||||
|
|
|
|
|
в |
окрестности |
точки |
x0 = 0 . |
Возьмем, |
||||||||
|
|
|
|
|
|
||||||||||||
|
|
x1 |
δ |
|
|
например, |
ε = 1 . |
Выберем любое значение |
|||||||||
|
|
|
|
δ > 0 . |
Для |
всех |
точек, |
для |
которых |
||||||||
|
–δ |
x2 |
|
x |
|||||||||||||
|
|
|
выполняется |
|
неравенство |
|
0 < x < δ, |
||||||||||
|
|
|
|
|
|
найдутся |
|
две |
|
точки |
|
x1 |
и |
x2 , |
|||
|
|
–1 |
|
|
|
принадлежащие интервалу |
(−δ;δ) |
такие, |
|||||||||
|
|
Рис.3.3 |
|
|
что |
|
f (x1 ) − f (x2 ) = 1−(−1) = 2 >1 |
(см. |
|||||||||
|
|
|
|
|
|
рис.3.3). |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
37 |
|
|
|
|
|
|
|
|
|
|

Во всех предыдущих рассуждениях число x0 – конечное число, т.е. x0 < ∞ . Возникает вопрос: как определить предел функции при неограниченном
возрастании |
x ? Поступим |
следующим образом: вместо аргумента x |
|||||||
рассмотрим аргумент t , связанный с x соотношением |
x = |
1 |
. Очевидно, если |
||||||
t |
|||||||||
t → 0 , то |
x →∞. Используем теперь определение 3.1 |
|
|
||||||
предела функции для |
|||||||||
1 |
|
при t → 0 : число |
A есть предел функции |
F(t) |
при t → 0 , если |
||||
F (t) = f |
|
|
|
||||||
|
|||||||||
t |
|
|
|
|
|
|
|||
для любого ε > 0 , существует δ > 0 такое, что при выполнении неравенства
0 < |
|
|
t |
|
|
< δ выполняется неравенство |
|
F (t ) − A |
|
< ε . |
x и учитывая, что |
||||||||
|
|
|
|
|
|||||||||||||||
|
|
||||||||||||||||||
|
1 |
|
Наконец, перейдя к исходной переменной величине |
||||||||||||||||
x = |
|
, получим определение предела на бесконечности: |
|
|
|
|
|
|
|
||||||||||
t |
|
|
|
|
|
|
x → ∞ , |
||||||||||||
|
|
|
|
Число A называют пределом функции |
f ( x) , при |
||||||||||||||
Определение 3.2. |
|||||||||||||||||||
если для любого |
ε > 0 существует δ > 0 такое, что, как только |
|
x |
|
> |
1 |
, так для |
||||||||||||
|
|
||||||||||||||||||
|
|
δ |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
всех x , удовлетворяющих этому неравенству выполняется соотношение |
|||||||||||||||||||
f(x) − A < ε .
Вопределении мы не уточняем, к какой бесконечности стремится переменная
x . Совершенно очевидно, что при x → +∞ требуется выполнение неравенства
x > |
1 |
|
, а при x →−∞ должно выполняться неравенство |
x < − |
1 |
. Тот факт, что |
|||||||||||
δ |
|
||||||||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
x , |
δ |
||||
число |
является |
пределом функции f (x) |
при |
стремящемся к |
|||||||||||||
бесконечности записывается следующим образом |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
lim f |
(x) = A . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
Очевидно, верно равенство |
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
lim |
|
= 0. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x 2 − 1 |
x→∞ x |
|
|
|
|
|
|||||
Пример 3.1. Докажем, что lim |
= 2 . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x →1 |
x − 1 |
|
|
|
|
|
|
|
|
|
||
Решение. Здесь функция |
x2 −1 |
не определена при x = 1. |
Но пока переменная величина x |
||||||||||||||
x −1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
стремится к 1 |
и не равна 1, |
можно сократить дробь |
x2 −1 |
= x +1 . Теперь найдём предел |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x −1 |
|
|
|
|||
lim (x +1) = 2 .
x→1
Предел последовательности
Используя предел функции при аргументе, стремящемся к бесконечности, можно определить предел последовательности. Для этого представим последовательность как функцию целочисленного аргумента. Этот аргумент
38

обычно обозначают буквой n . Значения функции y = f (n) обозначим при этом yn . Таким образом, числовая последовательность есть не что иное, как бесконечная последовательность чисел y1, y2 ,..., yn ,... , записываемая коротко {yn}. Используя определение предела функции при x , стремящемся к бесконечности, легко определить и предел последовательности.
Определение 3.3: Число A называют пределом последовательности {yn}, если для любого сколь угодно малого ε > 0 найдется натуральное число N такое, что для всех n > N выполняется неравенство yn − A < ε .
§3.2. Бесконечно малая величина и её свойства
Определение 3.4. Функция (величина) α( x) называется бесконечно малой при
x → x0 , если lim α(x) = 0 .
x→x0
Примеры бесконечно малых величин:
•α( x) = sin x , при x → kπ , где k - целое число;
•β( x) = cos x , при x → π2 + kπ , где k - целое число;
•γ(x) = x − 2 , при x → 2 .
Говорить о бесконечно малой величине можно только лишь подразумевая, что аргумент стремится к некоторому определенному значению, т.е. находится в окрестности некоторой определенной точки.
Имеется тесная связь между пределом и бесконечно малой величиной. Ниже будут доказаны две теоремы (прямая и обратная), на которых основаны доказательства основных свойств пределов.
Теорема 3.1 (прямая). Если функция f (x) при x → x0 имеет пределом число A , то в некоторой окрестности точки x0 функция представима в виде
f (x) = A + α(x) ,
где α( x) бесконечно малая величина при x → x0 .
Доказательство: По условию теоремы lim f (x) = A . Но тогда для произвольного
x→x0
сколь угодно малого ε > 0 , для всех x из некоторой окрестности точки x0 ( x ≠ x0 ) выполняется неравенство
f (x) − A < ε ,
а это означает, что lim ( f (x) − A) = 0 , т.е. f (x) − A = α(x) есть бесконечно малая
x→x0
величина в окрестности точки x0 . Отсюда следует, что f ( x) = A + α(x) ,
где α( x) - бесконечно малая при x → x0 . Теорема доказана.
39

Теорема 3.2 (обратная). Если |
функция |
f (x) |
в |
окрестности точки |
x0 , |
||||||||||||||
представима в виде |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = A + α(x) , |
|
|
|
|
|
||
где α(x) бесконечно малая величина при x → x0 , то |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim f ( x) = A . |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
x → x0 |
|
|
|
f ( x) − A = α(x) |
|
||
Доказательство. |
Из условия теоремы |
следует, |
что |
или |
|||||||||||||||
|
f (x) − A |
|
= |
|
α(x) |
|
. |
Так как α ( x) |
бесконечно малая величина, то для любого |
||||||||||
|
|
|
|
||||||||||||||||
ε > 0 , существует δ-окрестность |
точки |
x0 , такая, |
что |
для всех x из |
этой |
||||||||||||||
окрестности (как обычно, предполагается, что |
x ≠ x0 ) |
выполняется |
|||||||||||||||||
неравенство |
|
α(x) |
|
< ε . Отсюда |
вытекает, что |
для этой же |
δ -окрестности |
||||||||||||
|
|
||||||||||||||||||
справедливо неравенство
f (x) − A < ε .
Это и означает, что lim f (x) = A . Теорема доказана.
x→x0
При доказательстве основных свойств пределов нам потребуются свойства бесконечно малых величин, которые мы сейчас сформулируем и докажем.
Теорема 3.3. Сумма двух бесконечно малых величин есть бесконечно малая величина.
Доказательство. Пусть α( x) и β(x) |
бесконечно малые величины при x → x0 . |
||||||||||||||||||||||||||||||||||||||||||
Докажем, что их сумма ω(x) = α(x) + β(x) |
также бесконечно малая величина |
||||||||||||||||||||||||||||||||||||||||||
при x → x0 . |
|
Зафиксируем произвольное |
число |
ε > 0 , |
тогда |
найдется δ- |
|||||||||||||||||||||||||||||||||||||
окрестность точки x |
( 0 < |
|
x − x |
|
< δ) такая, что для всех x из этой окрестности |
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
выполняются неравенства |
ε |
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
α(x) |
|
< |
; |
|
β(x) |
|
< |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
и, следовательно, для всех x из этой |
|
|
же δ-окрестности |
|
выполняются |
||||||||||||||||||||||||||||||||||||||
соотношения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
ε |
|
|
|
|
|
|
|
ω(x) |
|
= |
|
α(x) +β(x) |
|
≤ |
|
α(x) |
|
+ |
|
β(x) |
|
< |
+ |
= ε , |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а это означает, что для всех x из данной |
δ -окрестности |
выполняется |
|||||||||||||||||||||||||||||||||||||||||
неравенство |
|
ω(x) |
|
< ε , т.е. ω(x) = α(x) + β(x) есть бесконечно малая величина |
|||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
при x → x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где α(x) , β(x) , γ(x) - бесконечно |
|||||||||||||||
Замечание. Если ω(x) = α(x) + β(x) + γ( x) , |
|||||||||||||||||||||||||||||||||||||||||||
малые при x → x0 , то, |
по только что доказанному, |
α(x) +β(x) = ∆(x) является |
|||||||||||||||||||||||||||||||||||||||||
бесконечно |
|
малой |
|
|
|
|
величиной |
|
|
|
при |
|
|
|
|
|
x → x0 |
|
|
и, |
следовательно, |
||||||||||||||||||||||
40
