Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Телекоммуникаций и Информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник

.pdf

Скачиваний:

103

Добавлен:

11.04.2015

Размер:

2.86 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 165 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

ω(x) = (α(x) + β(x)) + γ(x) = ∆(x) + γ(x) по той же теореме также бесконечно

малая величина при x → x0 .

Повторяя этот прием очевидно можно установить, что сумма любого конечного числа бесконечно малых величин является бесконечно малой величиной.

Теорема

3.4. Если функция

f ( x)

ограничена, а α(x)

бесконечно

малая

величина

окрестности

точки

x0 , то

произведение

f (x) α(x)

тоже

бесконечно малая величина при x → x0

Доказательство. Так как

f (x)

- ограничена, то существует число B такое,

что

f (x)

< B ,

тогда зафиксировав

ε > 0 , из того что α(x)

бесконечно малая

величина

окрестности

точки

можно

найти δ-окрестность точки

( 0 <

x − x0

< δ), такую, что

для

всех точек

этой окрестности выполняется

неравенство

α(x)

Оценим произведение функций

f (x)

и α(x) для любого значения x из этой

δ-

окрестности.

f ( x )α ( x)

f ( x )

α( x )

< B

= ε ,

и отсюда

f (x) α(x) бесконечно малая при x → x0 . Теорема доказана.

Теперь, пользуясь доказанными в этом пункте теоремами, сформулируем и

докажем основные свойства пределов.

§3.3. Свойства пределов

Теорема 3.5. Если пределы функций

f ( x) и

g(x) при x , стремящемся к x0 ,

существуют и конечны,

то при

x → x0 предел суммы этих функций равен

сумме пределов, т.е.

lim ( f (x) + g(x)) = lim f (x) + lim g(x) .

x→x0

Доказательство. По условию теоремы

< ∞,

< ∞ .

lim f (x) = A ; lim g (x) = B ;

x→x0

Тогда из теоремы 3.1 следует, что существует окрестность точки x0 такая, что функции f (x) и g (x) в окрестности точки x0 представимы в виде

f (x) = A + α(x) ; g(x) = B + β(x) ,

где α(x) и β(x) бесконечно малые. Следовательно

f (x) + g(x) = ( A + B) + (α(x) + β(x)) .

По теореме 3.3 сумма бесконечно малых также бесконечно малая, то есть α(x) + β(x) = γ(x) – бесконечно малая величина и, следовательно,

f (x) + g(x) = [ A + B] + γ(x) .

Из этого равенства и теоремы 3.2 следует, что

lim[ f ( x) + g (x)] = A + B .

x→x0

Отсюда и вытекает справедливость утверждения.

Совершенно очевидно, что теорема 3.5 справедлива при любом конечном числе слагаемых. Заинтересованному читателю предлагается самостоятельно установить этот факт.

Теорема 3.6. Если пределы функций f ( x) и g(x) существуют и конечны при x → x0 , то предел произведения этих функций равен произведению пределов этих же функций, т.е.

lim[ f (x) g(x)] = lim f (x) lim g (x) .
x→x0	x→x0			x→x0
Доказательство. По условию теоремы			A	< ∞,	B	< ∞ ,
lim f (x) = A ;	lim g (x) = B ,		A	< ∞,	B	< ∞ ,
x→x0	x→x0
x→x0	x→x0
и тогда по теореме 3.1 о связи предела с бесконечно малой получаем
f (x) = A + α(x) ; g(x) = B + β(x)
f (x) g(x) = ( A + α(x)) (B + β(x)) = A B + A β(x) + B α(x) + α(x) β(x) .
Используя теоремы 3.3 и	3.4, мы	можем			сказать, что величина

A β(x) + B α(x) + α(x) β(x) = γ(x) является бесконечно малой величиной при x → x0 . Отсюда получаем соотношение

f (x) g(x) = A B + γ(x) .

Тогда по теореме 3.2 о связи предела и бесконечно малой имеем

lim[ f (x) g (x)] = A B = lim f (x) lim g(x) .
x→x0	x→x0	x→x0
Теорема доказана.
Теорема 3.7. Если пределы функций	f (x) и	g(x) при x , стремящемся к x0 ,

существуют и предел g(x) отличен от нуля, то предел частного функций f (x) и g(x) равен частному пределов этих функций.

Доказательство теоремы аналогично доказательству теорем 3.5 и 3.6, поэтому приведем его в несколько сокращенном варианте. Согласно условиям теоремы в некоторой δ-окрестности точки x0 выполняются равенства

	lim f (x) = A ,			lim g (x) = B .
	x→x0			x→x0
Тогда
	f (x)	=	A + α(x)	=	A	+	B α(x) − A β(x)	,	(3.1)
			B + β(x)		B		B (B + β(x))
	g(x)

но B α(x) − A β(x) – бесконечно малая величина, потому что B α(x) − A β(x)

B (B + β(x))

– бесконечно малая, а B (B + β(x)) – ограниченная величина. Тогда из (3.1) и

теоремы 3.2 о связи предела и бесконечно малой величины получаем:

lim

x→x0

Теорема доказана.

f (x)

g(x)

	A		lim f (x)
=		=	x→x0
				.
	B		lim g(x)
			x→x0

Пример 3.2. Найти предел lim	x 2	+ 2	.
	x 2	+ 3
x → ∞

Решение. Разделим числитель и знаменатель на старшую степень переменной х, т.е. на x 2 и используем доказанные свойства предела:

+ 2

+ 2 ): x

1 +

lim

1 + 0

lim

= lim

x →∞

= 1 .

1 + 0

x →∞ x2 + 3

x →∞ (x2 + 3): x2

x→∞

lim

x →∞

§3.4. Свойства пределов, связанные с неравенствами

Теорема 3.8. Если для всех точек некоторой окрестности точки

x0 для

функций f (x) и F(x) выполняется неравенство f (x) ≤ F(x) и пределы f (x)

и F(x)

при x → x0 существуют, то

lim f (x) ≤ lim F (x) .

x→x0

Доказательство. Предположим, что

lim f (x) = A ;

lim F ( x) = B .

Наша

цель:

x→x0

доказать неравенство B ≥ A . Доказательство проведем методом от противного.

Допустим, что A > B .

Пусть A − B = C ,

и тогда,

положив ε =

, мы найдем

окрестность точки x0 , где при x ≠ x0

справедливы неравенства:

−

< f ( x) − A <

и −

< F (x) − B <

Тогда

f ( x) > A −

и F ( x) < B +

Следовательно

f ( x) − F (x) > A −

− B −

> 0 ,

что противоречит условию теоремы. Теорема доказана.

Теорема 3.9. Если для всех точек некоторой окрестности точки x0 для функций f (x) , F (x) , Φ(x) выполняются неравенства

Φ(x) ≤ f (x) ≤ F (x) .

Если при этом lim Φ(x) = lim F (x) = A , то предел f (x) существует и также
x→x0	x→x0

равен A .

Доказательство. Согласно предыдущей теореме

lim Φ(x) ≤ lim f ( x) ≤ lim F ( x)
x→x0	x→x0	x→x0

или

A ≤ lim f (x) ≤ A ,

x→x0

а это и означает, что lim f (x) = A . Теорема доказана.

x→x0

Существует еще одно утверждение, которым мы будем постоянно

пользоваться. Это утверждение часто называют признаком Вейерштрасса.

Доказательство его можно найти в полных курсах математического анализа.

Теорема 3.10.

(Признак Вейерштрасса). Если функция

f (x)

монотонно

возрастает при стремлении

к x0

и при этом ограничена сверху,

то она имеет

предел. Аналогично, предел существует у монотонно убывающей и

ограниченной снизу функции.

Все сформулированные выше утверждения справедливы и для

последовательностей. Мы предлагаем читателю самому сформулировать эти

утверждения для последовательностей и доказать их.

§3.5. Первый замечательный предел

Для вычисления пределов часто используют пределы, наиболее часто

применяемые при решении практических задач. В задачах теории связи часто

встречаются функции вида

f (x) = sin αx . Такая функция определена во всех

αx

точках числовой прямой за исключением x =0. При x , стремящемся к нулю, и

числитель, и знаменатель стремятся к нулю. Ответ на вопрос: “Чему равен

предел функции

sin αx

при х, стремящемся к нулю?” даёт нижеследующая

теорема.

αx

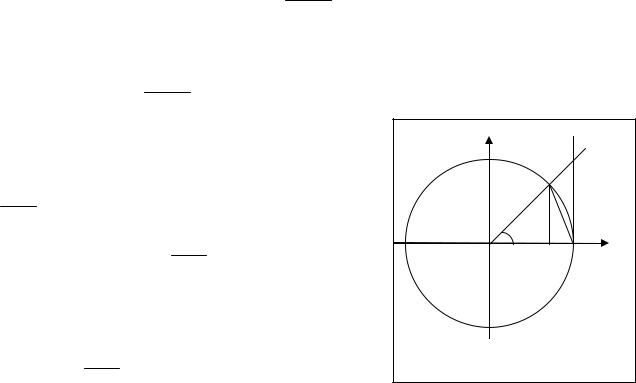
Теорема 3.11.

(Первый

замечательный

предел). При x,

стремящемся к нулю,

функция

sin x имеет предел, равный единице, т.е.

lim sin x =1.

x→x0

Доказательство. Докажем теорему, используя

геометрическую

интерпретацию

синуса

(рис.3.3). Так как

стремится

нулю и

функция

sin x

является четной,

то

можно

Рис. 3.3

от 0 до π

ограничиться изменениями

угла х в

пределах

(1-ой

четверти).

Рассмотрим окружность радиуса 1 и проведем луч ОА под углом х к оси

абсцисс.

Сравнивая

площади

треугольников с

вершинами

ОАС и ОСВ и

площадь сектора ОАС, заключаем

S∆OAC < Sсектор OAC < S∆OCB .

Но S∆OAC

sin x ,

Sсектор OAC

x ,

S∆OCB

tgx . Таким образом выполняются

неравенства

sin x <

x <

tg x .

Разделив

все части этого

неравенства

на

sin x , и помня, что sin x > 0 ,

получаем

1<		x	<	1	или	1 >	sin x	> cos x .
1<	sin x		<	cos x	или	1 >	x	> cos x .
	sin x			cos x			x
Перейдем к пределу при		x → 0 , учитывая, что						lim cos x =1, и теорему 3.9,
получим								x→0
получим					sin x
				lim	sin x	=1.
				lim	x	=1.
Теорема доказана.				x→0	x
Теорема доказана.

§3.6. Второй замечательный предел

Теорема 3.12. При	n,			стремящемся к бесконечности, числовая
последовательность yn			1	n
	= 1	+		имеет предел.

			n

Доказательство. Существование предела последовательности {yn}, при n → ∞

установим с помощью теоремы 3.10 (признака Вейерштрасса). Для этого нам нужно установить ограниченность этой последовательности и её монотонность.

Установим, прежде всего, монотонность этой последовательности. Согласно биному Ньютона имеем:

1 +

n(n − 1)

n(n − 1)(n − 2)

n(n −1)(n − 2)...(n − (n +1))

= 1 +

+ ... +

n 2

n n

1! n

n −1

= 1 + 1 +

−

1 −

−

+ ... +

−

1 −

−

(3.2)

Следующий член последовательности yn+1 равен

yn +1 = 1 + 1 +

n − 1

1 −

−

1 −

+ ... +

−

1 −

+ 1

n +

n + 1

1 −

+ 1)!

n +

n + 1

Сравнивая yn+1

и yn , мы видим, что каждое слагаемое yn+1 , начиная со второго,

больше соответствующего слагаемого yn . В самом деле,

−

1 −

;

n + 1

1			1			2		1			1			2
	1	−		1	−		>		1	−		1	−
3!								3!
			n + 1			n + 1					n			n

И так справедливо для каждого слагаемого

yn .

Последнее слагаемое в

выражении для

, а именно

очевидно также

n+1

(n +

1 −

−

+ 1

1) !

n + 1

положительно.

Таким образом,

yn+1 > yn

для

n =1, 2,...

и,

следовательно,

последовательность { yn } монотонно возрастает.

Докажем ограниченность этой последовательности. Так как

n (n − 1)...(n − k + 1)

≤ 1 ,

то из (3.2) имеем:

n k

(3.3)

1 +

≤

2 +

+ ... +

но

;

и так далее.

Известна сумма бесконечно

убывающей геометрической прогрессии:

+ ... +

+ … = 1 .

2 n

В нашем случае

2 2

+ ... +

< 1 .

n !

2 2

2 n

Отсюда и из (3.3) следует, что yn

< 3 .

Итак,

последовательность

монотонно возрастает и ограничена сверху,

поэтому на основании признака Вейерштрасса эта последовательность имеет предел. Этот предел обозначают буквой e.

			1 n
lim	1	+		= e .

n→∞			n

Это и есть второй замечательный предел, число e – иррациональное число, его приближенное значение равно 2,718 .

Мы установили второй замечательный предел						в предположении, что
аргументами функции				1 n	являются	натуральные числа.
аргументами функции	y(n) =	1	+		являются	натуральные числа.
				n

Спрашивается,

как будет

вести

себя предел

для функции непрерывного

аргумента, т.е. для функции

y( x) =

1 x

Теорема 3.13.

Предел функции

y ( x ) =

1 +

при x , стремящимся к

бесконечности, равен e , т.е.

1 x

1 +

= e .

lim

x→∞

Доказательство. Пусть x произвольное положительное число, тогда существует натуральное число n такое, что n ≤ x < n +1. Отсюда следует, что

1	>	1	>	1	или 1 +	1	≥ 1 +	1	> 1 +	1	.
n		x		n + 1		n		x
										n + 1

Так как аргумент х заключен между п и n +1, то из предыдущих неравенств имеем:

1 n +1

1 x

1 n

≥

n + 1

или

1 n

1 n +1

−1

(3.4)

1 +

≥

> 1

1 +

n + 1

В последнем выражении перейдем к

пределу

при

n → ∞ .

Тогда, по

предыдущей теореме,

1 n

n+1

= e .

lim

n + 1

Кроме того, имеем

n→∞

−1

1 +

= 1.

lim

n + 1

n→∞

Отсюда и из (3.4) вытекает справедливость утверждения теоремы. Докажем ряд следствий этой теоремы.

Следствие 3.13.1.

lim

1 +

= ea .

x→∞

Доказательство. Преобразуем выражение, стоящее под знаком предела,

a x

x a

1 +

(3.5)

Заметим, что

= e .

lim

= lim

1 +

x→ ∞

x → ∞

Отсюда и из (3.5) следует утверждение следствия. В частности,

lim 1 −

= e−1 .

Следствие 3.13.2.

x→∞

1 x

lim

= e .

x→ − ∞

Доказательство. Производя замену, сведём это утверждение к предыдущему:

− y

y − 1

− 1

lim (1 +

)

x = − y

lim

−

lim

−

( e

)

x → − ∞

y → ∞

Следствие 3.13.3.

lim(1 + x) x = e .

x→0

Доказательство. Подходящей заменой, утверждение сводится к утверждению теоремы 3.13:

1		1			1 t


lim(1 + x) x =	t =		= lim 1	+			= e .
		x
x→0			t→∞			t

§3.7. Сравнение бесконечно малых величин

Пусть α(x) и β(x) две бесконечно малые величины при x → x0 . Во

многих случаях представляет интерес сравнение бесконечно малых между собой по характеру стремления в нулю. Для этого рассмотрим предел

отношения этих величин при x → x , т.е. вычислим предел lim α(х)		. При этом
0	х→х0 β(х)
возможны следующие случаи:	х→х0 β(х)
возможны следующие случаи:
1. Предел отношения при x → x0 существует и равен постоянному числу
A ≠ 0 , т.е.	α(х) = А ≠ 0
lim	α(х) = А ≠ 0	(3.6)
х→х0	β(х)

В этом случае мы говорим, что бесконечно малые величины α(х) и β(х) одного

порядка и будем писать,		что	α(x ) = O (β(x))		(читается	«О большое») при
x → x . Например, при x → 0			функции α(x) = x2 и β(x) =1 − cos x являются
0
бесконечно малыми величинами одного порядка.
Если в равенстве (3.6) A =1, т.е.				α(х) =1,
			lim	α(х) =1,
			х→х0	β(х)
то будем говорить, что		α(x)и β(x) эквивалентные бесконечно малые
величины	при x → x0 и	будем писать α(x)~β(x) при				x → x0 .	Например,
α(x) = x2	и β(x) = tg2 x	при	x → 0	являются	эквивалентными		бесконечно

малыми.
2. Предел отношения α(x)и β(x)		при x → x0 существует и равен нулю:
	lim		α(х) = 0 .
В этом случае α(x)	х→х0		β(х)
	называют бесконечно малой более высокого порядка по
отношению к β(x)	и пишут α(x ) = o (β(x))			(читается «о малое»). Символ
o (β(x )) означает, что
	lim	o(β( х))		= 0 .
			β( х)
	х→ х0

Например, при x → 0 функция α(x) = x2 является бесконечно малой более высокого порядка по отношению к функции β(x) = x .

3. Предел отношения α(x) и β(x) равен бесконечности:

lim α( х) = ∞ .

х→ х0 β( х)

В этом случае β(x) является бесконечно малой более высокого порядка по отношению к α(x) и мы будем писать β(x) = o (α(x)). Так x = o(x ) при

x → 0 .

4. Предел отношения α(x) и β(x) не существует. В этом случае говорят, что бесконечно малые величины α(x) и β(x) несравнимы. Примером таких

величин являются функции α(x) = x sin

и β(x) = x при x → 0 . В самом деле,

α( х)

x sin

lim

= lim

= lim sin

β( х)

х → 0

х→ 0

х → 0

но этот последний предел не существует - в окрестности точки x = 0 функция sin 1x бесконечно много раз пробегает все значения от −1 до 1.

§3.8. Эквивалентные бесконечно малые величины и их свойства

Наиболее значимыми являются эквивалентные бесконечно малые

величины. Остановимся на них более подробно.

Согласно определению, α(x) и β(x) - эквивалентные бесконечно малые

величины ( α(x)~β(x)) при

x → x , если

lim α(x) = lim β(x) = 0 и, при этом,

x→x0

α(х) =1.

lim

х→х0

β(х)

sin x

Например, sin x ~ x при x → 0 , т.к. нами ранее доказано, что lim

=1.

х→0

Отношение эквивалентности обладает следующими свойствами.

Свойство 3.14 (симметричность). Если

α(x)~β(x) при x → x0 ,

то и

β(x)~ α(x) при x → x0 .

Доказательство. Пусть α(x)~ β(x) при x → x0 . Тогда

lim

β( х)

= lim

= 1,

α(х)

α(x)

α( x)

х→х0

x→x0

lim

β( x)

x→ x0

т.е., β(x)~ α(x) при x → x0 . Свойство доказано.

Отсюда,	в частности, следует, что если в окрестности точки x0 , x ≠ x0 ,
α(x) и β(x)	не имеют нулей, то они эквивалентны при x → x0 тогда и только
тогда, когда		α( х)		β( x)
	lim		= lim		= 1 .
		β( х)
	х→ х0		x→x0	α( x)

Свойство 3.15 (транзитивность). Если при x → x0 величины α(x)~ β(x) при

x → x0 , а β(x)~ γ(x) при x → x0 , то α(x)~ γ(x) при x → x0 . Доказательство. По условию

lim

α( х) = 1 и lim

β( х) = 1 ,

х → х0

β( х)

х → х0

γ( х)

но тогда

α(x)

α(х)

lim

= lim

β(x)

x→x0

β(x)

=1 .

γ(х)

γ(x)

х→х0

x→x0

lim

β(x)

x→x0

Свойство доказано.

Мы предлагаем читателю самостоятельно доказать следующее свойство. Свойство 3.16. Если при x → x0 выполняются отношения эквивалентности

α(x)~ β(x) и α1 (x)~β1 (x), то α(x) α1 (x) ~β(x) β1 (x).

Первый и второй замечательные пределы, полученные в предыдущем параграфе, позволяют нам составить таблицу эквивалентности для некоторых функций при x → 0 :

sin x x ;

tg x x ;

arcsin x x ;

arctg x x ;

−

cos x

х2

−

1 x ;

2 ;

ln (1+ x) x ;

(1 + x)α 1 + αx .

Вторая эквивалентность вытекает из равенства tg x =

sin x и предела

cos x

lim

= 1 . Третья и четвертая эквивалентности, по сути, повторяют первую

cos x

х→0

и вторую для соответствующих обратных функций (свойство 3.14).

Для

доказательства

асимптотического

равенства

заметим, что

1− cos x = 2sin2

, а так как sin

то, по свойству 3.16,

из предыдущего

соотношения вытекает доказываемая эквивалентность.

Асимптотическое равенство 6 вытекает из свойства 3.13.3:

ex −1 = lim(1

+ x) x

−1 = lim(1+ x) x

−1 = lim(1+ x) −1 x .

x→0

<<< < Предыдущая 1 2 3 45 / 165 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.09.201940.89 Кб5ДЗ Экология 1 курс.docx
#
11.04.20153.6 Mб175Диплом Баженов испр. М.Л.М..doc
#
11.04.2015213.11 Кб77диплом2.docx
#
11.04.20151.35 Mб115Дискретная_матем1.doc
#
11.04.2015836.61 Кб31Дискретная_матем2.doc
#
11.04.20152.86 Mб103ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник.pdf
#
11.04.2015183.81 Кб12ДКБ Реферат.doc
#
11.04.20153.48 Mб43ДМ Практикум.pdf
#
11.04.2015518.14 Кб29ДМ_гл1_DO.doc
#
16.09.2019501.25 Кб3ДМ_гл1_TM_чит.doc
#
11.04.2015484.86 Кб13ДМ_гл2_DO.doc