Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Телекоммуникаций и Информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник

.pdf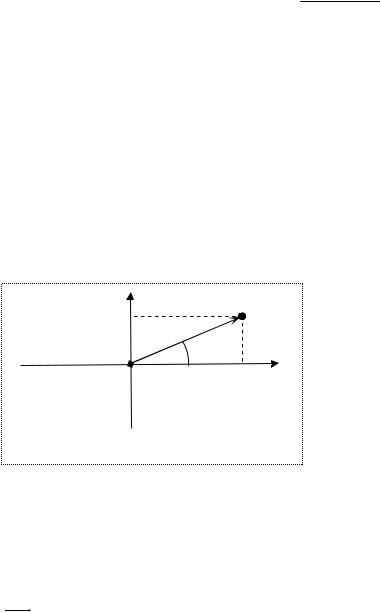

Скачиваний:

103

Добавлен:

11.04.2015

Размер:

2.86 Mб

Скачать

☆

<<< < Предыдущая 12 / 162 3 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

z2 – z1 = (2 + 5i) – (-1 + 6i) = 3 – i.

Частное находим по формуле (1.6):

z2	=	2 + 5i	=	(−1) 2 + 6 5	+	(−1) 5 − 2 6	i =	28	−	17	i .
z		−1 + 6i		(−1)2 + 62
						(−1)2 + 62		37 37
1

Пример 1.3. Выполнить действия

3 + i

(1 + i)(1− 2i) .

Решение. Перемножив числа, стоящие в знаменателе, получим

z =	3 + i	=	3 + i	=	3 +i	.
	+i)(1− 2i)		− 2i +i + 2
(1		1			3 −i

Далее поступим так же, как в примере 1.1. Тогда

z =	(3	+i)(3 +i)	=	9 + 6i −1	=	4	+	3	i .
	(3	−i)(3 +i)		9 +1		5
								5

§1.4. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числа.

Тригонометрическая форма записи комплексного числа


Каждому комплексному		числу	a + bi	может быть		поставлена			в
y	z		соответствие		точка			M (a;b)
			координатной		плоскости	и,	наоборот,
b		М
			каждой точке M (a;b) плоскости можно
φ	a	x	соотнести	комплексное		число		a + bi .
O			Установленное		таким		образом
			соответствие		является		взаимно
			однозначным. Оно дает возможность
Рис. 1.4			рассматривать		комплексные		числа		как
			точки координатной плоскости.					Такую

плоскость называют комплексной плоскостью. При этом ось абсцисс называют действительной осью (на ней расположены точки, соответствующие действительным частям комплексного числа), ось ординат – мнимой осью (на ней лежат точки, соответствующие мнимым частям комплексного числа).

Используя взаимосвязь между точками плоскости и векторами, комплексное число a + bi удобно интерпретировать геометрически как вектор OM (рис.1.4). Каждому вектору плоскости с началом в точке O (0; 0) и с концом в точке M (a;b) соответствует комплексное число a + bi и наоборот.

Точке O (0;0) соответствует нулевой вектор.

Опираясь на установленное взаимно-однозначное соответствие и не боясь путаницы, мы будем комплексное число z называть также точкой или вектором z.

Изображение комплексных чисел векторами позволяет дать простое геометрическое истолкование операциям над комплексными числами. Например, сумма комплексных чисел геометрически может быть истолкована

как вектор,	равный сумме векторов,				y
соответствующих			слагаемым

комплексным числам (рис.1.5).
Определение		1.7.	Модулем
комплексного числа			называется длина
соответствующего		этому		числу	z2
вектора.				z	O
Для	модуля		числа
					Рис. 1.5
используется обозначение \|z\|. Модуль

комплексного числа z = a + bi может быть вычислен по формуле z = 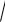a2 + b2 .

z1+z2

(1.7)

Определение 1.8. Аргументом комплексного числа z ≠ 0 называется угол между положительным направлением действительной оси и вектором z, причем этот угол считается положительным, если отсчет ведется против часовой стрелки, и отрицательным, если отсчет производится по часовой стрелке. Для числа z = 0 аргумент не определяется.

Аргумент комплексного числа, в отличие от модуля, определяется

неоднозначно. Например, аргументами числа						z =1 + i являются	каждый из
углов φk =	π +2πk, где k – произвольное целое число. Будем называть главным
значением	4	−π < ϕ ≤ π.
	аргумента угол				Для	обозначения аргумента числа
z = a + bi	используется символ Arg z				(будем	также употреблять букву φ).
Главное значение аргумента обозначим arg z . Таким образом,
	ϕ = Arg z = arg z + 2πk, k = 0,±1, ±2,…						z = a + bi
Действительная и мнимая части комплексного числа
выражаются через его модуль			z	= r и аргумент φ следующим образом:

				a = r cos ϕ			(1.8)

				b = r sin ϕ

Следовательно, комплексное число z = a + bi можно записать в виде
z = r (cos ϕ + i sin ϕ).							(1.9)
Такая форма записи называется тригонометрической формой записи
комплексного числа.
Аргументы φ комплексного числа могут быть найдены из формул
			a
cos ϕ =						b
cos ϕ =
	a2 + b2				или tg ϕ =		(1.10)
	a2 + b2				или tg ϕ =		(1.10)
		b				a
sin ϕ =		b				a
sin ϕ =
	a	2	+ b	2
	a		+ b

Так как −π < arg z ≤ π, то получаем

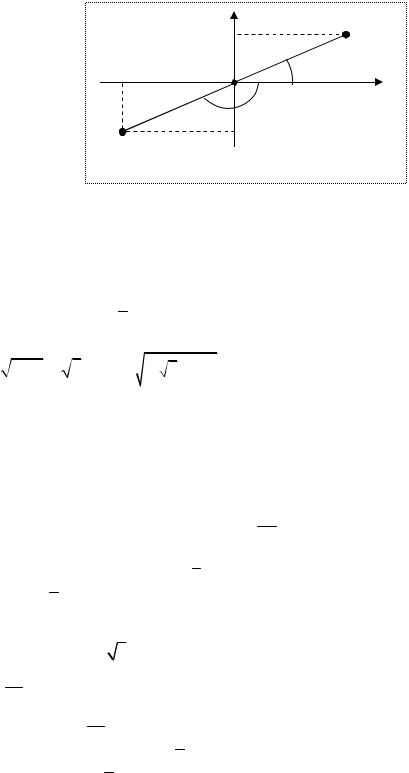
	b		если a > 0
arctg		,
arctg	a	,
	a
	b
	b		если a < 0, b ≥ 0 ,	(1.11)
arg z = arctg		+ π,
arg z = arctg	a	+ π,
	a
	b	− π, если a < 0, b < 0
arctg
arctg	a
	a

На рис.

1.6

точки

М1

М2

расположены

симметрично

относительно

начала

координат.

М1

Комплексное

число,

- a

соответствующее точке М1 ,

имеет

аргумент,

равный

φ,

число,

- b

изображенное

точкой

М2 ,

имеет

М2

аргумент, равный

ϕ− π.

Рис. 1.6

Для точек z, лежащих на

действительной оси,

arg z = 0

при a > 0 и arg z = π при

a < 0 .

Если точка z

лежит на мнимой оси, то arg z = π

при b > 0 и arg z = −

при b < 0 .

Пример 1.4. Найти модули комплексных чисел

z1 = 2 – i, z2 = 2 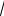6 + 5i, z3 = i.

Решение. По формуле (1.14) находим

|z1| = 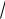4 +1 = 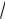5 , |z2| = 26 2 + 52 = 7 .

Для вычисления модуля z3 нет необходимости использовать формулы (1.7). Длина вектора z3 = i, очевидно, равна единице и поэтому |z3| = 1.

Пример 1.5. Найти аргументы комплексных чисел

z1 = -i, z2 = 1, z3 = -1 + i.

Решение. Построив векторы z1, z2, z3, находим один из аргументов для каждого числа: φ1 = -π/2, φ2 = 0, φ3 = 3π/4. Следовательно,

Arg z1 = − π2 + 2πk , Arg z2 = 2πk , arg z3 = Arg z3 = 34π + 2πk ,

где k – произвольное целое число.

Пример 1.6. Найти аргументы комплексного числа z = -1 – 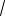3 i. Решение. В данном случае a = -1, b = – 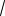3 i. Система (1.10) имеет вид

cos ϕ = −1/ 2

sin ϕ = − 3 / 2

Решив эту систему, найдем ϕk = − 23π + 2πk, k Z . Следовательно,

Arg z = − 23π + 2πk, k Z

Пример 1.7. Найти аргументы комплексного числа z = − 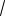3 + i .

Решение. Каждый из аргументов φ числа z = − 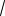3 + i удовлетворяет уравнению

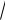tg z = −1/ 3 .

Из этого уравнения следует, что
			ϕk = − π			+ πk, k Z .
		6
	Так как число z = −		+ i расположено во втором квадранте комплексной плоскости,
		3
то его аргументами будут числа φk при нечетных значениях k. Следовательно,
			Arg (−		+ i) =		5π	+ 2πn, n Z
				3
							6
§1.5. Умножение комплексных чисел в тригонометрической форме.
			Формула Муавра
	Тригонометрическая форма записи комплексных чисел особенно удобна
при	умножении и	делении чисел.				Пусть z1 = r1 (cos ϕ1 + i sin ϕ1 ) и
z2 = r2 (cos ϕ2 + i sin ϕ2 )		– два числа, записанные в тригонометрической форме.
Тогда
z1 z2	= r1r2 ((cos ϕ1 cos ϕ2 − sin ϕ1 sin ϕ2 ) + i (sin ϕ1 cos ϕ2 + cos ϕ1 sin ϕ2 )).

Используя тригонометрические формулы суммы углов, получим

z1 z2 = r1r2 (cos(ϕ1 + ϕ2 ) + i sin (ϕ1 + ϕ2 )),

(1.12)

Таким образом, модуль произведения двух комплексных чисел равен произведению модулей этих чисел, сумма аргументов сомножителей является аргументом произведения. В частности, при z1 = z2 = z имеем

z2 = r 2 (cos 2ϕ + i sin 2ϕ)

Обобщая на общий случай возведения комплексного числа в натуральную

степень, получим формулу Муавра
(r (cos ϕ + i sin ϕ))n = r n (cos nϕ + i sin nϕ)	(1.13)

Она показывает, что при возведении комплексного числа в целую положительную степень, модуль возводится в эту степень, а аргумент умножается на показатель степени.

Если положить r =1, то формула примет вид

(cos ϕ + i sin ϕ)n = cos nϕ + i sin nϕ,

откуда вытекают, в частности, тригонометрические формулы тройных углов: cos 3ϕ = cos3 ϕ− 3cos ϕsin2 ϕ; sin 3ϕ = −sin3 ϕ+ 3cos2 ϕsin ϕ.

При делении комплексных чисел в тригонометрической форме, используя аналогично тригонометрические формулы, получим

z1		=	r1	(cos (ϕ1 − ϕ2 )+ i sin (ϕ1 − ϕ2 )).	(1.14)
			r
z	2
		2

Таким образом, модуль частного двух комплексных чисел равен частному модулей этих чисел, разность аргументов делителя и делимого является аргументом частного.

Пример 1.8. Найти произведение и частное двух чисел

			z		=							cos							3π			+ i sin						3π		и z			=				cos							−		3π			+ i sin				−	3π			.
									2										3π									3π								8										3π								3π
									2																							2				8
		1																		4												2
																				4								4																			8							8
Решение. Так как			z1		=								,			z2				=						, то			z1z2		= 4 , а					z1			=		1		. Аргументом произведения z z

										2														8																																			2
										2														8
																																				z2			2																		1
																																				z2			2
будет сумма ϕ + ϕ =							3π		−					3π			=				3π		. Поскольку ϕ −ϕ =																			3π			+		3π		=	9π		= 2π−				7π		, то аргументом
1		2			4				8											4													1		2				4							8					8			8
				z1	4				8											4																			4							8					8			8
частного будет				z1							7π				. Таким образом
частного будет	arg z2					= − 8									. Таким образом
	arg z2					= − 8
					z z				=									cos							3π		+ i sin			3π		,		z1	=			1		cos						−		7π			+i sin			−	7π		.
																8									3π					3π				z1				1										7π							7π
								2								8
					1			2																4
																								4						4 z2								2										8								8

Пример 1.9. Записать в тригонометрической форме комплексное число

z =

(cos(π / 3) − i sin(π / 3))(

+ i)

z = cos π

−i sin π

i −1

ϕ = − π

Решение.

Число

имеет

модуль, равный

1, и

аргумент

; число

= π ; число z

+ i

имеет модуль 2 и аргумент ϕ

= i −1 имеет модуль

и аргумент

3π

− ϕ3 = − π

+ π −

3π

ϕ3 =

. Поэтому

а аргумент

ϕ = ϕ1 + ϕ2

= −

π .

Следовательно,

z =

cos

−

+ i sin

−

π .

Пример 1.10. Возвести в девятую степень комплексное число z =

−i .

Решение. Модуль числа z

равен 2, а одним из аргументов является угол ϕ = −π / 6 , поэтому

модуль числа z9 равен 29 , а аргумент числа z равен 9ϕ = −3π / 2 . Следовательно,

(

− i)9 = 29 (cos(−3π / 2) + i sin(−3π / 2)) = 512i .

§1.6. Извлечение корня степени n

Число w называется корнем степени n из числа z (обозначается n

если wn = z .

Например,

числа

= i

и w2

= −i

являются корнями

второй степени

(квадратными корнями) из числа z = −1, так как i2 = −1 и (−i)2

= −1.

Из определения корня вытекает, что каждое решение уравнения

wn = z

является корнем степени

n из числа

z .

Другими словами, для того чтобы

извлечь корень степени n из числа z , достаточно решить уравнение wn = z . Это уравнение имеет n решений (корней степени n из z ), которые, если использовать тригонометрическую форму записи (1.9), могут быть найдены по формуле

= n

cos

ϕ+ 2πk

+i sin

ϕ+ 2πk

, k = 0,1, , n −1.

(1.15)

В правильности этой формулы нетрудно убедиться, возводя каждое из

чисел wk в степень n. Из формулы (1.15)

видно,

что все корни степени

n из

числа z имеют один и тот же модуль n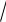r , но разные аргументы, отличающиеся друг от друга слагаемым, кратным числу 2π/ n . Отсюда следует, что комплексные числа, являющиеся корнями степени n из числа z , соответствуют точкам комплексной плоскости, расположенным в вершинах правильного n-

угольника, вписанного в окружность радиуса n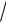r с центром в точке О.

Таким образом, символ n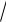z не имеет однозначного смысла. Поэтому, употребляя его, следует четко представлять себе, что под этим символом

подразумевается. Например, используя запись 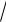−1, следует позаботиться о том, чтобы было ясно, понимается ли под этим символом число i или число −i , или же пара этих чисел.

Пример 1.11. Найти все значения 4−16 .

Решение. Запишем число z = −16 в тригонометрической форме

z = −16 =16(cos π + i sin π) . Согласно формуле (1.15) получаем

w	= 2	cos	π + 2πk	+ i sin	π + 2πk	, . k = 0,1, 2,3

k
			4		4

Следовательно,


w0	= 2	(cos (π / 4) + i sin (π / 4)) =		+ i						,
			2						2
w1 = 2(cos (3π / 4) + i sin (3π / 4)) = −								+ i								,
						2							2
w2	= 2	(cos(5π / 4) + i sin (5π / 4)) = −						− i							,
						2						2
w3	= 2	(cos(7π / 4) + i sin (7π / 4)) =					− i							.
					2						2

На рис.1.7 изображены все четыре значения 4−16 . Точки, соответствующие числам ω0 , ω1 , ω2 , ω3 , находятся в вершинах квадрата, вписанного в окружность радиуса R = 2 с центром в точке z = 0 .


Пример 1.12. Записать число	5 +12i			−	5 −12i	в
Пример 1.12. Записать число			+			в
	5	+12i	+		5 −12i

	y
w1	w0
	2	x
	2
w2	w3
	Рис. 1.7

алгебраической форме при условии, что действительные части корней 5 +12i и 5 −12i отрицательны.

Решение. Для извлечения квадратного корня из числа 5 +12i положим 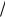5 +12i = x + iy , тогда 5 +12i = x2 + 2xyi − y2 и, следовательно, x и y удовлетворяют системе уравнений

x2 − y2 = 5,

xy = 6.

Решив систему, получим два решения (3; 2 ) и (−3; −2 ) . По условию действительная часть 5 +12i отрицательна, поэтому 5 +12i = −3 − 2i . Аналогично найдем

5 −12i	= −3 + 2i . Таким образом,
		−3 − 2i − (−3 + 2i) 2
	z =	−3 − 2i + (−3 + 2i)	=		i .
				3

Для закрепления материала решите самостоятельно следующие примеры и задачи.

1.1. Представить комплексное число z

в тригонометрической форме:

z = −

+i .

б) z = −1.

z = −cos

а)

в)

− i sin

10π

г)

z =1 + cos

+ i sin

. д)

z = tg1− i .

1.2.

Записать

комплексное

число

в алгебраической и

тригонометрической формах:

а)

z =

i (cos (5π/ 3) + i sin (5π/ 3))

б)

z =

cos (π/ 6)+ i sin (π/ 6)

cos (4π/ 3)− i sin (4π / 3)

в)

д)

а)

г)

z =

г)

z =

−cos (

5π/12) + i sin (5π/12)

(1+i)2

cos (13π /12)− i sin (13π/12)

− i sin

+ i

cos

z =

1.3. Записать комплексное число z

в алгебраической форме:

−10

z =

−

б)

z = (cos 3

+ i sin 3 )

. в) z

z = −

(2i)7

(1+ i)9

. д)

z =

(1− i )7 .

(−

+ i

а)

1.4. Записать комплексное число z в тригонометрической форме:

							6			2n+1
							6			2n+1
		100						в) z = (1	+ i )2n−1 , n N .
z = (	3 −i )	100			3i +1
			б) z =		3i +1	.
			б) z =	i −1		.
				i −1				1	− i	)
								(		)

1.5. При каких целых значениях n справедливо равенство (1 + i )n = (1− i )n ?

1.6. Найти все значения n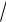z , если:

z = i , n = 2 . б) z = −1, n = 3. в) z = 8i , n = 3.

Глава 2. Функция

§2.1. Понятие функции. Способы задания функции

Идея зависимости одних величин от других возникла, по-видимому, на заре становления науки. Однако четкие математические определения появились гораздо позже. Например, Л. Эйлер описывал функцию так: «Величины, зависящие от других так, что с изменением вторых меняются и первые, принято называть их функциями». Таким образом, одни величины считаются независимыми переменными, а другие – зависимыми, т.е. функциями.

Например, изучая прямолинейное движение с постоянным ускорением, мы имеем дело с такими величинами как время t, ускорение a, начальная скорость V0. Функциями же служат путь S, пройденный за время t или скорость в момент времени t , т.е. величины, которые зависят от значения величин t, a, V0. Эта зависимость выражается формулами

S =	at2	+V t; V = at +V .

	2	0	0

Другой пример: в формуле Эйнштейна E = m c2			энергия E зависит от массы m

– независимой переменной. Рассмотрим более подробно случай, когда функция зависит только от одного независимого переменного. Дадим строгое определение функции.

Определение 2.1. Пусть D - некоторое подмножество действительных чисел. Предположим, что каждому числу x D ставится в соответствие единственное число y, согласно некоторому правилу. В таком случае будем говорить, что на множестве D задана однозначная функция или просто функция. Этот факт запишем в виде: y = f ( x) , где f обозначает конкретный вид этого правила

Множество D назовем областью определения функции f (x) . Величину x

называют независимой переменной или аргументом; переменную y называют

функцией (зависимой переменной).

Множество всех значений функции y = f ( x) , x D , будем называть образом множества D (или областью значений функции) и обозначать E( f ).

E = f (D) ={y | y = f (x), x D}

Говорят, что функция f отображает D на множество f (D) . Если f (D) A , то будем говорить, что f отображает D в A. Следует отметить, что

символ f (x) обозначает число	y,	которое соответствует числу	x, x D .
Например, если x0 D , то f (x0 )	-	значение функции в точке x0 ;	если же

x0 D , то мы говорим, что функция f не определена в точке x0 .

Для функций f и g заданных на одном и том же множестве D определены

функции:	сумма	f + g ; разность f − g ;		произведение	f g ;	частное	f / g .
Значения	новых	функций	определены, соответственно,			выражениями:
f (x) + g(x) , f (x) − g(x) ,			f (x) g (x) ,	f (x) / g(x) . В	последнем		случае
предполагается, что g(x) ≠ 0 .

Рассмотрим способы задания функций.

Одним из самых распространенных является аналитический способ, т.е. определение функции с помощью формулы. Например,

		y =	x3	+ 4	; y = sin3 4x .
y = 1 − x2 ; y = log	(1 + x) ;
			x2	− 2
3

В дальнейшем будем рассматривать только действительные функции, т.е. функции действительного независимого переменного, принимающие действительные значения. Все действительные значения независимой переменной, при которых определена функция, называют естественной областью определения функции.

Всякий раз, когда находится область определения функции, это, как правило, естественная область определения. Например, функция y = 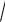1 − x2

имеет областью определения отрезок	[	]	y = log	3	(1	+ x)
		−1,1 , а функция

определена на полубесконечном интервале (−1,+∞).

Приведенные примеры определяют функцию явно. Примером неявного

задания функции может служить	уравнение	x2 + y2 =1. В общем	случае
уравнение F (x, y) = 0 определяет	неявно	заданную функцию y	от x ,

независимо от того, возможно или невозможно разрешить это уравнение относительно y, т.е. получить из него уравнение y = f ( x) .

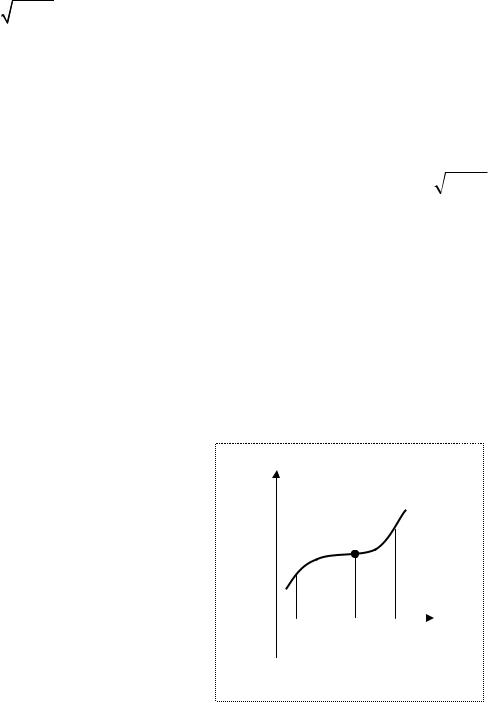
Другим возможным способом задания функции является графический способ.

На плоскости задается декартова система координат xOy . На оси Ox возьмем

отрезок [a,b] и изобразим некоторую

кривую Г, которая обладает следующим свойством: любая прямая, параллельная оси

Oy и проходящая через x [a,b] пересекает

Г ровно в одной точке А (рис.2.1). В этом случае кривую Г называют графиком.

График определяет функцию y = f (x)

О a

x b

согласно	следующему	правилу:	Рис. 2.1
произвольной	точке x [a,b]	ставится в	Рис. 2.1
произвольной	точке x [a,b]	ставится в
соответствие	значение	y = f (x)

определяемое как ордината точки A

Аналогичным образом функция определяется графически на интервале, на всей числовой оси, на объединении двух отрезков и т.д. Если функция f (x)

задана графически на (a,b), то достаточно просто получить графики следующих функций:

					y = 3f(x)		y	y = f(x)+c
							y
		3
					y = f(x)		2	y = f(x)+2
	a	1	0		x	a	0		x
			0	b	x	a	0	b	x
		Рис. 2.2					Рис. 2.3
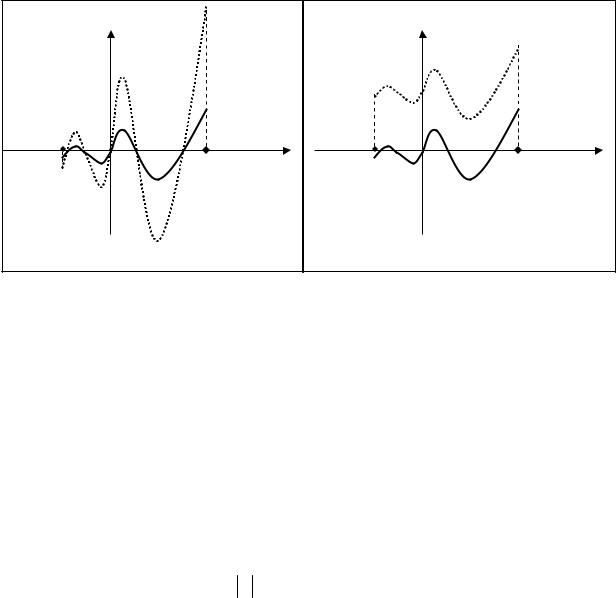
1)	α f (x)		- сжатие (при α <1) или растяжение (при α >1) графика по оси

Oy ;

2)	f (x) + α - сдвиг графика вверх (при α > 0 ) или вниз (при α < 0 ) по оси
Oy ;
3)	f (x − α) - сдвиг графика вправо (при α > 0 ) или влево (при α < 0 ) по
оси Ox ;	f (α x) - сжатие (при α >1) или растяжение (при α <1) графика по оси
4)

Oy .

Заметим, что графики функций 1) и 2) определены на том же интервале (a,b), что и f (x) . Ординаты графика функции 1) получаются из ординат графика функции f (x) умножением на число α. Ординаты графика функции 2) получаются из ординат графика f (x) сдвигом последних вверх на величину α, если α > 0 , и сдвигом вниз на α , если α < 0 (рис.2.2 и 2.3).

График функции 3) получается из исходного сдвигом вправо на α, если

α > 0 , и сдвигом на	α	,	если α < 0 . И наконец, график функции 4) при α > 0

определен на интервале			a	,	b	. График функции	y = f (α x) получается из


			α		α

исходного равномерным сжатием его в α раз по оси x (рис.2.4 и 2.5).

<<< < Предыдущая 12 / 162 3 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.09.201940.89 Кб5ДЗ Экология 1 курс.docx
#
11.04.20153.6 Mб175Диплом Баженов испр. М.Л.М..doc
#
11.04.2015213.11 Кб77диплом2.docx
#
11.04.20151.35 Mб115Дискретная_матем1.doc
#
11.04.2015836.61 Кб31Дискретная_матем2.doc
#
11.04.20152.86 Mб103ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник.pdf
#
11.04.2015183.81 Кб12ДКБ Реферат.doc
#
11.04.20153.48 Mб43ДМ Практикум.pdf
#
11.04.2015518.14 Кб29ДМ_гл1_DO.doc
#
16.09.2019501.25 Кб3ДМ_гл1_TM_чит.doc
#
11.04.2015484.86 Кб13ДМ_гл2_DO.doc