
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Трофимов Агульник
.pdf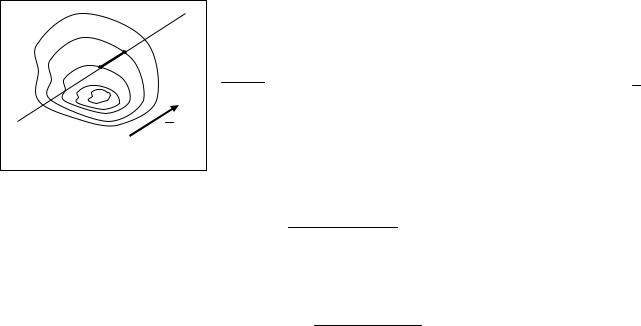
|
§3.2. Производная по направлению |
|
|
|
|
|
|
|
|
|
||||||||||
Пусть задано скалярное поле u(M ) . Обычно представляет интерес |
||||||||||||||||||||
скорость изменения этой величины по заданному направлению. Зададим |
||||||||||||||||||||
произвольную прямую l , и возьмем на ней некоторую точку M 0 |
(рис.3.2). Для |
|||||||||||||||||||
любой переменной точки M на этой прямой рассмотрим направленный отрезок |
||||||||||||||||||||
|
|
|
M 0 M . Будем считать его положительным, если его |
|||||||||||||||||
М |
|
l |
направление совпадает с направляющим вектором |
|||||||||||||||||
|
прямой, |
и |
отрицательным |
– |
в |
противном |
случае. |
|||||||||||||
|
|
|||||||||||||||||||
М0 |
|
|
Другими словами, отрезок |
M 0 M > 0, если векторы |
||||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
M0M |
и |
направляющий |
вектор |
прямой |
|
|
l |
||||||||||
|
l |
|
сонаправлены |
и |
M 0 M |
|
< |
0, |
|
если |
|
они |
||||||||
|
|
противоположно направлены. |
|
|
|
|
|
|
|
|
|
|
||||||||
Рис.3.2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Пусть M неограниченно приближается к M 0 |
. Если |
|
||||||||||||||||
|
|
|
|
|||||||||||||||||
при этом существует предел |
|
u(M ) − u(M 0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
M |
→M0 |
|
MM 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разностного отношения, то этот предел называется производной по направлению |
||||||||||||||||||||
l от функции u(M ) |
и обозначается символом |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
∂u |
= lim |
u(M ) − u(M 0 ) . |
|
|
|
|
|
|
|
|
|
(3.1) |
|||||
|
|
|
∂l |
M |
→M0 |
MM0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это определение производной по направлению носит инвариантный |
||||||||||||||||||||
характер, т.е. не связано с выбором системы координат. Если же задана система |
||||||||||||||||||||
координат, то можно вывести расчетную формулу для вычисления производной |
||||||||||||||||||||
скалярного поля по заданному направлению. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Теорема 3.1. Производная скалярного поля u( x, y, z) |
по направлению l |
в точке |
||||||||||||||||||
M 0 (x0 ; y0 ; z0 ) равна |
|
∂u |
= ∂u cos α + |
∂u cosβ + |
∂u cos γ , |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
(3.2) |
||||||||||||
|
|
|
∂l |
∂x |
|
∂y |
|
∂z |
|
|
|
|
|
|
|
|
|
|
||
где ∂u , ∂u , ∂u - частные производные функции u( x, y, z) |
в точке M |
0 |
(x ; y |
; z |
0 |
) , |
||||||||||||||
∂x ∂y ∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а cos α, cosβ, cos γ - направляющие косинусы единичного вектора el. |
|
|
|
|
|
|
|
|||||||||||||
Доказательство. |
В |
|
стандартной |
системе |
координат |
Oxyz |
|
|
векторы |
|||||||||||
el = (cosα, cosβ, cos γ) |
и |
M0M = (x − x0 , y − y0 , z − z0 ) |
коллинеарны. |
|||||
Следовательно, выполняются равенства |
|
|
|
|
||||
|
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
|
|
cos α |
cosβ |
|
|
|||
|
|
|
|
cos γ |
|
|||
Обозначая это общее отношение через t, координаты текущей точки M (x; y; z) можно представить в виде:
x = x0 + t cos α , y = y0 + t cosβ, z = z0 + t cos γ .
131

Таким образом, функция u( x, y, z) представляется как сложная функция, а её
приращение |
u(M ) − u(M 0 ) = ∆u , |
вызванное |
приращением независимой |
|||||||||
переменной t равно |
|
|
|
|
|
|
|
|
|
|
|
|
∆u = |
∂u(x, y, z) |
|
∂x |
∆t + |
∂u(x, y, z) |
∂y |
∆t + |
∂u(x, y, z) |
|
∂z |
∆t + o(∆t) , |
|
|
∂x |
|
∂t |
|
∂y |
|
∂t |
|
∂z |
|
∂t |
|
где все частные производные вычисляются при t = 0 ( x = x0 , y = y0 , z = z0 ), а o(∆t) - бесконечно малая более высокого порядка, чем ∆t при ∆t = t → 0 . Отсюда
∆u |
= |
∂u cos α + ∂u cosβ + ∂u cos γ + |
o(∆t) |
. |
|
|
|||||
∆t |
|
|
|
||||||||
|
∂x |
∂y |
∂z |
|
∆t |
|
|
||||
Переходя к пределу в формуле (3.1), получим |
|
|
|
|
|
||||||
|
|
∂u |
= lim |
|
∆u |
= lim |
∆u = |
|
|
||
|
|
∂l |
|
MM 0 |
|
|
|||||
|
|
M →M0 |
|
∆t→0 |
∆t |
|
|
||||
= cos α lim ∂u(x, y, z) + cosβ lim ∂u(x, y, z) + cos γ lim |
∂u(x, y, z) |
= |
|||||||||
t→0 |
∂x |
|
|
t →0 |
∂y |
|
t →0 |
∂z |
|
||
|
|
= ∂u cos α + |
|
∂u cosβ + ∂u cos γ , |
|
|
|||||
|
|
∂x |
|
|
∂y |
∂z |
|
|
|||
где частные производные вычисляются в точке M0. Теорема доказана.
Пример 3.2. Найти производную поля u = x2 + y2 − 4 yz в точке M0 (0;1;2) в направлении от этой точки к точке M1 (2;3;3) .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Находим вектор M0M1 и его направляющие косинусы |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
= (2; 2; 1) |
, cos α = |
2 |
; |
|
cosβ = |
2 |
; |
|
cos γ = |
1 |
. |
||||||||||
|
|
|
M 0 M1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
||||||
∂u |
|
= 2x |
|
|
|
= 0 ; ∂u |
|
|
= 2 y − 4z |
|
|
|
|
= −6 ; ∂u |
|
= −4y |
|
= −4 . |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
∂x |
|
M0 |
|
M0 |
∂y |
|
|
|
|
|
|
|
M |
0 |
∂z |
|
M0 |
|
|
|
M0 |
|||||
|
|
|
M 0 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Применяя формулу (3.2), получим |
∂u = − |
16 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
∂l |
3 |
|
|
|
|
|
|
|
|
|
|
||||
Так как ∂∂ul < 0 , то поле в данном направлении убывает.
§3.3. Градиент
Пусть имеется скалярное поле, определяемое дифференцируемой скалярной функцией
u = u(x, y, z)
Градиентом скалярного поля u в данной точке М называется вектор, обозначаемый символом grad u, и определяемый равенством
grad u = i |
∂u |
+ j |
∂u |
+ k |
∂u |
= |
∂u |
; |
∂u |
; |
∂u |
. |
(3.3) |
|
∂x |
|
∂y |
|
∂z |
∂x |
|
∂y |
|
∂z |
|
|
|
132
Если el - единичный вектор в направлении l, то производная по направлению l |
|||||||||||
связана с этим вектором следующим соотношением: |
|
|
|
|
|
|
|
|
|||
|
|
∂u = gradu e . |
|
|
|
|
|
|
(3.4) |
||
|
|
∂l |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
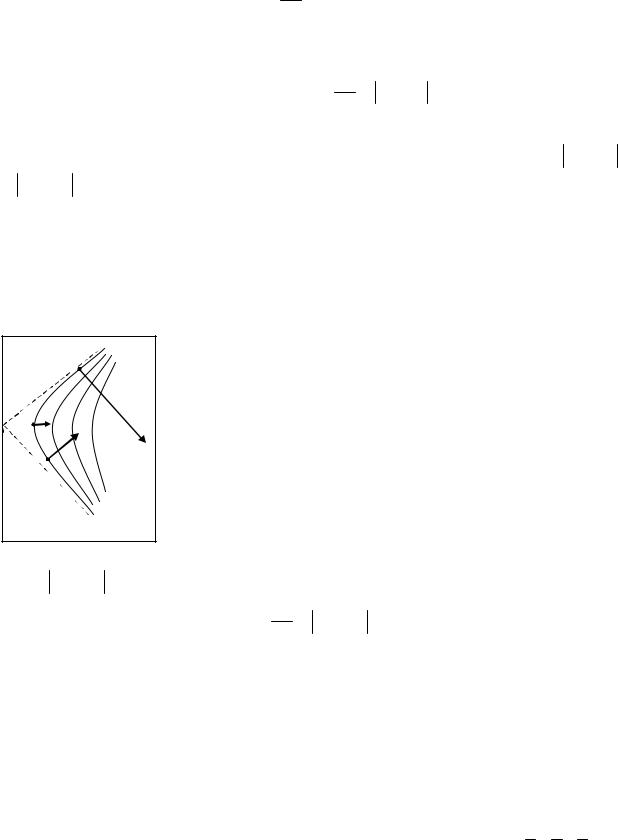
Градиент скалярного поля обладает двумя основными свойствами. |
|
|
|||||||||
Первое: его абсолютная величина определяет наибольшую скорость |
|||||||||||
изменения поля. Действительно, так как ∂u |
= gradu cos ϕ, где φ – угол между |
||||||||||
|
|
∂l |
|
|
|
|
|
|
|
ϕ = π ÷ |
|
векторами grad u |
и el, то при ϕ = 0 получаем наибольшую, |
а при |
|||||||||
наименьшую скорости изменения поля, |
равные |
соответственно |
grad u |
и |
|||||||
− grad u . |
|
|
|
|
|
|
|
|
|
|
|
На рис.3.3 градиент построен в трёх разных точках, лежащих на одной |
|||||||||||
линии уровня (см. пример в разделе 3.1). |
|
|
|
|
|
|
|
|
|
||
Второе свойство градиента состоит в том, что он направлен по нормали к |
|||||||||||
поверхности (линии) уровня. В самом деле, рассмотрим разность ∆u двух |
|||||||||||
поверхностей уровня и разностные отношения ∆u |
и |
∆u , где ∆n |
и ∆l |
– |
|||||||
|
|
|
∆n |
|
∆l |
|
|
|
|
||
|
положительные приращения вектора нормали n и |
||||||||||
|
произвольного направления l в некоторой точке |
||||||||||
|
поверхности уровня. Так как длина нормали меньше |
||||||||||
|
длины |
наклонной, |
то ∆u > |
∆u . |
|
Поскольку |
|
предел |
|||
|
|
|
∆n |
∆l |
|
|
∂u |
> ∂u . |
|
|
|
|
сохраняет знак неравенства, |
имеем |
|
То есть, |
|||||||
|
|
|
|
|
|
|
∂n |
∂l |
|
|
|
|
наибольшая скорость возрастания поля с одной стороны |
||||||||||
Рис. 3.3 |
равна ∂u |
, с другой стороны, согласно первому свойству, |
|||||||||
|
|||||||||||
|
∂n |
|
|
|
|
|
|
|
|
|
|
равна grad u . Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u = grad u , |
|
|
|
|
|
|
|
|
|
|
|
∂n |
|
|
|
|
|
|
|
|
|
откуда следует, что grad u ↑↑ n . Если же grad u ↑↓ n , |
то вектор n указывает |
||||||||||
направление наибольшей скорости убывания поля. |
|
|
|
|
|
|
|
|
|||
Другие свойства градиента: |
|
|
|
|
|
|
|
|
|
||
|
grad (u + v) = grad u + grad v , |
|
|
|
|
|
|
|
|
||
grad cu = cgrad u , где с – постоянная, |
(3.5) |
grad uv = v grad u + u grad v . |
|
Эти свойства выводятся из определения градиента.
Пример 3.3. Найти наибольшую скорость возрастания скалярного поля u = xy + yz + xz в точке
A (-1; 1; -1).
Решение. Вычислим градиент поля
133

|
1 |
|
|
z |
|
|
x |
1 |
|
|
|
y |
|
1 |
||||||||
grad u = |
|
− |
|
|
|
i + − |
|
|
|
+ |
|
j + |
|
− |
|
|
+ |
|
k . |
|||
|
|
|
2 |
y |
2 |
z |
z |
2 |
|
|||||||||||||
|
y x |
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||
Его значение в точке А: |
grad u (−1;1; −1) = 2i − 2k . |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
Таким образом, наибольшая скорость возрастания поля равна |
|
|
|
|
||||||||||||||||||
|
|
|
|
grad u (A) |
|
= 2 |
|
|
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||
Пример 3.4. Найти градиент скалярного поля u = x – 2y +3z. Решение. Согласно формуле (3.3) имеем
grad u = i – 2j +3k.
Поверхностями уровня данного скалярного поля являются плоскости x − 2 y + 3z = C ; вектор
grad u = (1, −2, 3) есть нормальный вектор плоскостей этого семейства.
Пример 3.5. Найти единичный вектор нормали к поверхности уровня скалярного поля u= x2 + y2 + z2.
Решение. Поверхности уровня данного скалярного поля – сферы x2 + y2 + z2 = C ( C >0 ).
Градиент направлен по нормали к поверхности уровня, так что grad u = 2xi + 2yj + 2zk
определяет вектор нормали к поверхности уровня в точке М(x, y, z). Для единичного вектора нормали получаем выражение
en = |
grad u |
|
= |
xi + yj + zk |
|
|
= |
r |
. |
|
| grad u |
| |
|
|
|
|
|
||||
|
x2 + y2 + z |
|
||||||||
|
|
|
2 |
|
|
| r | |
||||
§3.4. Касательная плоскость и нормаль к поверхности
В этой главе мы рассмотрим некоторые геометрические вопросы исследования функции нескольких переменных, использующие результаты предыдущей главы. Покажем, в частности, что дифференцируемость функции
z = f (x, y) в точке M0 (x0 ; y0 ) с геометрической точки зрения означает наличие касательной плоскости к графику функции z = f (x, y) в точке N0 (x0 ; y0 ; z0 ) .
Введем |
|
понятие |
|
|
|
|
|
|
|
|
|||
касательной |
плоскости |
к |
|
z |
|
|
поверхности в точке N0 . Будем |
|
N1 |
N2 |
|||
предполагать, |
что в этой точке, |
|
|
|||
а также в |
некоторой |
её |
x0+ x |
|
N0 |
|
окрестности, |
|
функция |
|
|||
|
|
|
||||
определена, |
непрерывна |
и |
|
|
|
|
дифференцируема. |
|
|
x0 |
|
|
|
Плоскость, |
проходящая |
|
M0 |
|||
через точку |
N0 |
поверхности, |
|
|
||
|
|
|
||||
называется |
|
касательной |
|
|
y0 y0+Δy |
|
плоскостью в этой точке, |
если |
|
Рис. 3.1 |
|||
|
|
|||||
угол между этой плоскостью и |
|
|
||||
|
|
|
||||
секущей |
|
плоскостью, |
|
|
|
|
134
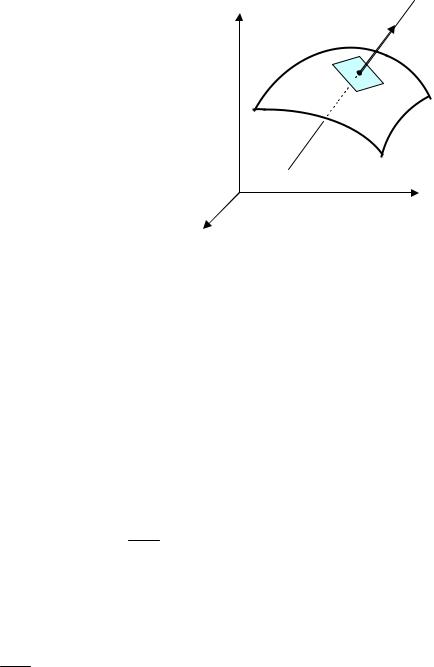
проходящей через точку N0 и любую точку N, поверхности, стремится к нулю,
когда точка N стремится к N0 . |
|
|
|
|
|
|
|
|||||||||
Положим ∆x = x − x0 , ∆y = y − y0 , ∆z = z − z0 , где z0 = f (x0 , y0 ), |
z = f (x, y). |
|||||||||||||||
Тогда |
условие |
дифференцируемости |
|
|
|
|
|
|||||||||
|
|
|
|
|
||||||||||||
можно записать в виде: |
|
|
|
|
|
|
|
|
|
n |
||||||
|
z − z0 = A(x − x0 ) + B( y − y0 ) + γ , |
|
|
|
|
|||||||||||
|
A = |
∂z |
(M 0 ), B = |
∂z |
|
(M 0 ), |
|
|
|
|
|
|
||||
где γ |
∂x |
∂y |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
– |
бесконечно |
|
|
малая |
при |
|
|
|
|
|
||||||
∆x → 0, ∆y → 0 |
более высокого |
порядка, |
|
|
|
|
|
|||||||||
чем ∆x и ∆y . |
|
z1 = f (x0 + ∆x, y0 ), |
|
|
|
|
|
|||||||||
Пусть |
|
|
|
|
|
|
||||||||||
z2 = f (x0 , y0 + ∆y). |
Рассмотрим |
секущую |
|
|
|
Рис. 3.2 |
|
|||||||||
плоскость P, |
проходящую |
|
|
через |
точки |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
N0 (x0 ; y0 ; z0 ) , |
N1 (x0 + ∆x; y0 ; z1 ) |
и |
N2 (x0 ; y0 + ∆y; z2 ). Используя |
уравнение |
||||||||||||
плоскости, проходящей через три данные точки, получим |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
x − x0 |
y − y0 |
|
z − z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
∆x |
0 |
|
∆x z |
|
= 0 , |
|
|
где ∆x z = f (x0 + ∆x, y0 ) − f (x0 |
|
0 |
|
∆y |
|
∆y z |
|
|
|
|||||||
, y0 ), ∆y z = f (x0 , y0 + ∆y) − f (x0 , y0 ) . |
|
|||||||||||||||
Приводя уравнение плоскости N0 N1N2 |
к общему виду, получим |
|
||||||||||||||
|
|
−∆x z ∆y (x − x0 ) − ∆y z ∆x ( y − y0 ) + ∆x ∆y (z − z0 ) = 0 . |
||||||||||||||
Разделим обе части последнего равенства на величину (−∆x ∆y):
∆∆xxz (x − x0 ) + ∆∆yyz (y − y0 )− (z − z0 ) = 0 .
При стремлении точек N1 и N2 к N0 , секущая плоскость становится
касательной плоскостью. При этом
∆x → 0, ∆y → 0 ,
∆∆xxz → z′x (M 0 ), ∆∆yyz → z′y (M0 ).
Тогда уравнение касательной плоскости примет вид
A(x − x0 ) + B( y − y0 ) − (z − z0 ) = 0 .
Нормальный вектор
n= ∂∂xz ; ∂∂yz ; −1
касательной плоскости определяет уравнение нормали, т.е. прямой, перпендикулярной касательной плоскости и проведенной через точку касания.
135
Уравнение этой нормали к поверхности в точке N0 (x0 ; y0 ; z0 ) имеет вид:
|
x − x0 |
= |
|
y − y0 |
= |
z − z0 |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
∂z (M 0 ) |
|
|
∂z |
(M 0 ) |
|
−1 |
|
|
|
|
|
|
|
|
|
|||||
|
∂x |
|
|
∂y |
|
|
|
|
|
|
В случае неявного задания функции F (x, y, z ) = 0 , коэффициенты z′ |
и |
z′ |
||||||||
|
|
|
|
|
|
|
|
x |
|
y |
вычисляются по формулам (2.8), и тогда уравнение касательной плоскости удобнее переписать в виде
F′(M |
0 |
) (x − x ) |
+ F′(M |
0 |
) ( y − y ) + F′(M |
0 |
) (z − z |
) = 0 , |
||||||
x |
0 |
y |
|
|
0 |
z |
0 |
|
||||||
а уравнение нормали |
|
x − x |
|
|
|
y − y |
|
z − z |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
= |
|
0 |
= |
0 |
. |
|
|
|||
|
|
|
Fx′(M 0 ) |
Fy′(M 0 ) |
Fz′(M 0 ) |
|
|
|||||||
Пример 3.1. Составить уравнение касательной плоскости и нормали к поверхности,
задаваемой неявно равенством |
|
x |
|
= x2 |
− y + |
z2 |
|
|
в точке M0 (1;1) . |
|
|
|
|
|
||||||||||||||||||||
|
z |
|
|
y |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. Из уравнения поверхности, подставляя x0 |
=1 и |
y0 =1 , найдём значение z0 =1. |
||||||||||||||||||||||||||||||||
|
F (x, y, z ) |
= z |
− x |
|
+ y − |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Имеем |
|
|
|
|
|
x |
|
|
2 |
|
z2 |
. Найдём частные производные |
|
|
|
|
|
|||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
F′(M |
|
) = |
|
F′(M |
|
) = 1 + |
|
z2 |
|
|
|
, F′(M |
|
) = − |
x |
|
2z |
|
= −3 . |
|||||||||||||||
|
− 2x |
= −1, |
|
|
|
= 2 |
|
− |
|
|||||||||||||||||||||||||
|
x |
0 |
|
z |
|
|
|
M 0 |
|
|
|
y |
|
0 |
|
|
|
|
y2 |
|
M 0 |
z |
0 |
|
z2 |
|
y |
|
M 0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, уравнение касательной плоскости имеет вид |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
−(x −1) + 2 ( y −1) − 3 (z −1) = 0 или x − 2y + 3z + 2 = 0 . |
|||||||||||||||||||||||||||
Уравнение нормали к поверхности в точке N0 (1;1;1) |
имеет вид |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x −1 |
= |
|
y −1 |
= |
z −1 |
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
−3 |
|
|
|
|
|
|
|
||||||||
Замечание. Формулы касательной плоскости и нормали к поверхности получены для обыкновенных, т.е. не особых, точек поверхности. Точка M0
поверхности называется особой, если в этой точке все частные производные равны нулю или хотя бы одна из них не существует. Такие точки мы здесь рассматривать не будем.
§3.5. Экстремум функции двух переменных
Понятие максимума и минимума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной.
Пусть |
функция z = f (x, y) определена в некоторой области D, |
точка |
M (x0 ; y0 ) D . |
|
|
Точка |
(x0 ; y0 ) называется точкой максимума функции z = f (x, y) , |
если |
существует такая δ-окрестность точки (x0 ; y0 ) , что для каждой точки (x; y) , отличной от (x0 ; y0 ) , из этой окрестности выполняется неравенство f (x, y) < f (x0 , y0 ) .
136
Точка (x0 ; y0 ) называется точкой минимума функции z = f (x, y) , если существует такая δ-окрестность точки (x0 ; y0 ) , что для каждой точки (x; y) , отличной от (x0 ; y0 ) , из этой окрестности выполняется неравенство
f (x, y) > f (x0 , y0 ) .
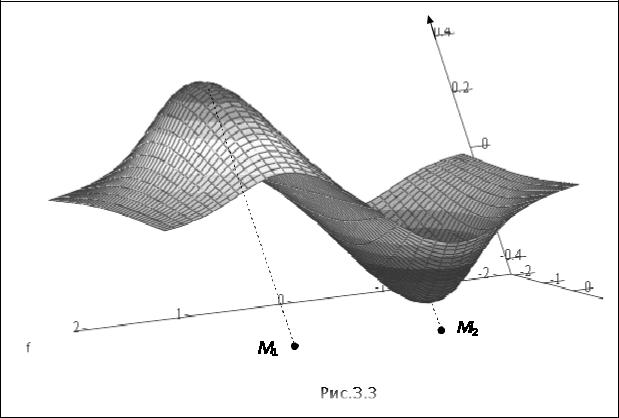
Рисунок 3.3 получен с помощью программы MatLab, причем для наглядности поверхность показана в косоугольной системе координат. Здесь M1 - точка максимума, а M2 - точка минимума функции.
z
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции являются её экстремумами.
Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке (x0 ; y0 ) сравнивается с ее
значениями в точках, достаточно близких к (x0 ; y0 ) . В области D функция может иметь несколько экстремумов или не иметь ни одного.
Пусть функция z = f (x, y) задана в некоторой области D и M0 (x0 ; y0 ) – точка экстремума этой функции. Пусть ∆z = f (M ) − f (M0 ) - полное
приращение функции, где M – произвольная точка области D в указанной окрестности точки M 0 . Тогда при ∆z < 0 в точке M 0 имеем максимум, а при
∆z > 0 – минимум.
137

Теорема 3.1 (необходимый признак экстремума) Пусть функция z = f (x, y)
имеет в точке M0 (x0 , y0 ) экстремум. Тогда, если в этой точке существуют
частные производные первого порядка, то эти частные производные равны нулю.
∂z
Доказательство. Докажем равенство нулю частной производной ∂x . Положим
y = y0 и получим функцию z = f (x, y0 ) одной переменной х. Очевидно, эта функция имеет в точке x = x0 экстремум. Согласно необходимому признаку
экстремума функции одной переменной производная ∂∂xz (M0 ) = 0 . Рассуждая аналогично, получим ∂∂yz (M 0 ) = 0 . Теорема доказана.
Данный необходимый признак не является достаточным. Например, частные производные по x и y функции z = xy в точке M0 (0;0) равны нулю, но
экстремума в этой точке нет, так как в окрестности её есть как положительные, так и отрицательные значения функции. Поэтому будем считать точки, в которых частные производные равны нулю, как точки возможного экстремума -
стационарные точки.
Теорема 3.2 (достаточный признак экстремума). Пусть в точке M0 (x0 ; y0 ) и
некоторой ее окрестности функция z = f (x, y) дважды дифференцируема и все производные непрерывны. Пусть
|
|
|
∂z |
(M |
0 ) = 0 и |
|
∂z |
(M |
0 ) = 0 . |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
Положим |
|
|
∂x |
|
|
|
∂y |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
∂2 z |
(M |
|
), |
B = |
∂2 z |
|
(M |
0 |
) |
, C = |
∂2 z |
(M |
0 |
). |
|||
|
0 |
∂xdy |
|
|
||||||||||||||
|
∂x2 |
|
|
|
|
|
|
|
|
∂y2 |
|
|||||||
Тогда, если в точке возможного экстремума M 0 |
выполнены условия: |
|||||||||||||||||
а) B2 − AC < 0 , то в этой точке есть экстремум. При |
A > 0 – минимум, |
|||||||||||||||||
при A < 0 – максимум. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) B2 − AC > 0 , то в этой точке нет экстремума. (В этом случае говорят:
M 0 есть точка минимакса).
Доказательство. Воспользуемся формулой Тейлора
∆z (M0 ) = dz |
|
+ |
1 |
d 2 z |
|
+ … + |
1 |
d n z |
|
+ |
1 |
|
d n+1z |
|
. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|||||||||||||||||
|
|
|
(n +1)! |
|
||||||||||||||
|
|
M0 |
2! |
|
M0 |
n! |
|
M0 |
|
|
M1 |
|
||||||
Так как точка M 0 – точка возможного экстремума функции z , то dz |
|
M0 |
= 0 |
|||||||||||||||
|
||||||||||||||||||
|
|
|||||||||||||||||
(по необходимому признаку экстремума). Оставляя в формуле Тейлора бесконечно малые второго порядка, получим:
138

|
|
|
1 |
|
|
|
1 |
|
|
2 |
z |
|
|
|
2 |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∆z (M |
|
) = |
d 2 z |
|
= |
|
|
∂ |
|
|
∆x2 + 2 |
∂ |
|
|
∆x∆y + |
||||
0 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2! |
|
M 0 |
2! |
|
∂x2 |
|
|
|
∂x∂y |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
M 0 |
|
|
|
|
|
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Перепишем это выражение в следующем виде:
|
∆z (M 0 ) = |
1 |
(A∆x2 |
+ 2B∆x∆y + C∆y2 )= |
∆y |
2 |
|
∆x |
2 |
|
||||
|
|
A |
|
+ |
||||||||||
|
2 |
2 |
|
∆y |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Полагая |
∆x |
= t , получим ∆z |
(M0 ) = |
∆y2 |
(At 2 |
+ 2Bt + C ). |
|
|
|
|||||
|
∆y |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
∂ |
2 |
z |
|
|
|
|
|
||||
|
|
|
∆y2 . |
||
∂y |
2 |
|
|
|
|
|
|
M 0 |
|
||
|
|
|
|
||
2B ∆∆xy + C .
Определим знак ∆z (M0 ) |
по |
знаку |
правой |
части |
квадратного |
трехчлена |
|||
At2 |
+ 2Bt + C . |
Пусть дискриминант |
D = B2 |
− AC |
квадратного |
уравнения |
|||
At2 |
+ 2Bt + C = 0 меньше нуля. |
Тогда уравнение не имеет корней и сохраняет |
|||||||
знак: при A > 0 |
этот |
знак |
положителен, |
при |
A < 0 – отрицателен. |
||||
Следовательно, |
при |
A > 0 |
∆z(M0 ) > 0 и функция имеет минимум, |
при A < 0 |
|||||
∆z(M0 ) < 0 и функция имеет максимум в точке M 0 .
Если B2 − AC > 0 , то квадратный трехчлен не сохраняет знак, и экстремума нет. Заметим, что при D = 0 необходимо дополнительное исследование.
Пример 3.2. Найти экстремумы функции z = 1 + 6x − x2 − xy − y2 .
Решение. Находим частные производные:
∂∂xz = 6 − 2x − y ; ∂∂yz = −x − 2 y .
Для определения стационарных точек запишем систему уравнений:
6 − 2x − y = 0;
−x − 2 y = 0.
Решая эту систему, получим одну точку, координаты которой: x0 = 4 ; y0 = −2 . Вторые частные производными постоянны:
A = |
∂2 z |
= −2 ; B = |
∂2 z |
= −1 |
; C = |
∂2 z |
= −2 . |
|
∂x2 |
∂x∂y |
∂y2 |
||||||
|
|
|
|
|
||||
Следовательно, B2 − AC = −3 < 0 |
и экстремум существует. |
Так как A = −2 < 0, то точка |
||||||
M 0 (4; −2) - точка максимума данной функции. При этом zmax =13 . Пример 3.3. Найти экстремумы функции z = x4 + y4 − 2 x2 + 4xy − 2 y2 .
Решение. Находим частные производные:
∂∂xz = 4x3 − 4x + 4 y ; ∂∂yz = 4 y3 + 4x − 4 y .
Приравнивая частные производные к нулю и решая полученную систему уравнений, найдём
три стационарные точки: M 0 (0; 0 ) ; M1 ( |
|
|
|
|
|
|
; |
|
). |
|
||||
2; − 2 ); M 2 (− |
|
|||||||||||||
2 |
2 |
|
||||||||||||
Найдём вторые частные производные: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 z |
2 |
|
|
|
∂2 z |
∂2 z |
|
|
|
|
2 |
|
||
∂x2 =12x |
|
− 4 ; |
|
= 4 ; ∂y 2 |
= 12 y |
|
− 4 . |
|||||||
|
∂x∂y |
|
||||||||||||
Подставляя координаты стационарных точек в выражение (B 2 − AC ), получим: |
||||||||||||||
Для точки M 0 (0;0) A = −4; B = 4; C = −4; |
D = 0 . |
|
|
|
|
|
|
|||||||
139

Для точки M1 ( |
|
|
|
|
|
|
|
) |
A = 20 > 0; B = 4; C = 20; |
D = B 2 − AC = 384 > 0 . |
2; − |
2 |
|||||||||
Для точки M2 (− |
|
|
|
|
) |
A = 20 > 0; B = 4; C = 20; |
D = B2 − AC = 384 > 0 . |
|||
2; |
2 |
|||||||||
Таким образом, |
точки M1 и M 2 - точки минимума функции. В этих точках значения |
|||||||||
функции одинаковы и равны zmin = −8 . В точке M 0 нужны дополнительные исследования.
Однако, очевидно, эта точка не является точкой экстремума. В самом деле, в этой точке z = 0 , а в любой окрестности этой точки значения z могут быть как положительными, так и
отрицательными. Например, вдоль оси Ох (т.е. |
при y = 0 ) |
z = x4 − 2 x2 |
= −x2 (2 − x2 ) < 0 |
||||
вблизи |
начала |
координат, |
а |
вдоль |
прямой |
y = x |
имеем |
z = x4 + x4 − 2x2 + 4x2 − 2x2 = 2x4 > 0 . |
|
|
|
|
|
||
Для закрепления материала решите самостоятельно следующие примеры и задачи.
Для заданной функции z = f(x, y) и точки A найти:
a)дифференциал z в точке A;
b)касательную и нормаль к поверхности z = f(x, y) в точке A;
c)экстремумы функции z.
3.1. |
z = xy + y2 − 2x, A(1; 2) |
3.2. |
z = 2x2 +2xy − y2 , |
A(1; 3) |
|
3.3. |
z = x2 + 3xy + y2 , |
A(1;2) |
3.4. |
z = x2 − xy + y2 , |
A(1; 3) |
3.5. |
z = x − y − x2 − y2 , |
A(−2; 2) |
3.6. |
z = xy + 2x − y, A(2; 2) |
|
3.7. Найти поверхности уровня скалярных полей
а) u = |
x2 |
+ |
y2 |
+ |
z2 |
, б) u = z − x2 − y2 , в) u = |
|
. |
|
x + y + z |
|||||||||
a2 |
b2 |
c2 |
|||||||
|
|
|
|
|
|
3.8. Найти линии уровня скалярных полей:
а) u = x2 + y2 , б) u = x2 − y , в) u = x2 − y2 , г) u = x + y . a2 b2
3.9.Дано скалярное поле u = x2 + y2 , Найти grad u в точке (3;2).
3.10.Дано скалярное поле u = 
 4 + x2 + y2 , Найти grad u в точке (2;1).
4 + x2 + y2 , Найти grad u в точке (2;1).
3.11.Дано скалярное поле u = arctg xy , Найти grad u в точке (x0 ; y0 ).
3.12. Каково направление наибольшего изменения в начале координат функции u(x, y, z) = xsin z − y cos z ?
|
1 |
|
равен i − |
16 |
j . |
|
3.13. Найти точку, в которой градиент функций u = ln x + |
|
|
|
|
||
|
9 |
|||||
|
y |
|
|
|||
3
3.14. Найти точки, в которых модуль градиента функции z = (x2 + y2 )2 равен 2.
3.15. Найти производную функции и = x3 − 3x2 y + 3xy2 +1 в точке М(3; 1) в
направлении, идущем от этой точки к точке (6; 5).
3.16. Найти производную функции и = arctg(xy) в точке (1; 1) в направлении биссектрисы первого координатного угла.
140
