
- •1.Матрица.Транспонированная матрица.Сложение и умножение на число.
- •2Отрицательная матрица
- •3Элементарные преобразования матрицы.Вырожденные и невырожденные.
- •4 Минора и алгеброические дополнения
- •6 Обратная матрица
- •7Ранг матрицы
- •Связанные определения
- •8Системы линейных уравнений
- •9Система линейных уравнений решение методом гаусса
- •10Решение системы с помощью обратной матрицы
- •11Кривые второго порядка
- •12Окружность
- •13Элиппс
- •14Гипербола
- •15Парабола
- •17Дифференци́рованием.
- •[Править] Определение производной функции через предел
- •18Правила дифференцирования
- •19Производная обратной функции
- •20Правило диференц. Сложн. Функ.
- •21И22 на листке.
- •23Производные от обратных тригонометрических функций
- •24Дифференциал
- •25Производные и дифференциалы высших порядков
- •26Дифференцирование функций, заданных параметрически
- •27Теорема Ферма
- •28И29Теоремы Ролля, Лагранжа, Коши
- •30Тейлора формула
- •31Раскрытие неопределенностей. Правило Лопиталя
- •32Точки экстремума
- •Необходимое условие экстремума
- •Достаточное условие экстремума
- •Общий план исследования функции и построения графика.
- •35Неопределенный интеграл и его свойства. Таблица интегралов.
- •36Метод замены переменной (метод подстановки)
- •Интегрирование по частям
- •37Интегрирование рациональных выражений
- •38Эйлера подстановки
- •39Определения
- •41Определения
- •Стандартная модель
- •Матричная модель
- •Замечания
- •Модуль и аргумент
- •Сопряжённые числа
- •Алгебраическая форма
- •Тригонометрическая и показательная формы
- •42Геометрическая интерпретация комплексного числа
17Дифференци́рованием.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.
Пусть
в некоторой окрестноститочки
![]() определенафункция
определенафункция
![]() Производной
функции называется такое число
Производной
функции называется такое число
![]() ,
что функцию в окрестностиU(x0)
можно представить в виде
,
что функцию в окрестностиU(x0)
можно представить в виде
f(x0 + h) = f(x0) + Ah + o(h)
если
![]() существует.
существует.
[Править] Определение производной функции через предел
Пусть
в некоторой окрестноститочки
![]() определенафункция
определенафункция
![]() Производной
функцииfв точкеx0называетсяпредел,
если он существует,
Производной
функцииfв точкеx0называетсяпредел,
если он существует,
![]()
[править] Общепринятые обозначения производной функции y = f(x) в точке x0
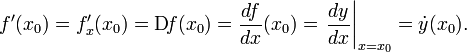
Заметим,
что последнее обычно обозначает
производную по времени (в теоретической
механике).Производная
![]() функцииfв точкеx0, будучи пределом,
может не существовать или существовать
и быть конечной или бесконечной. Функцияfявляется дифференцируемой в точкеx0тогда и только тогда, когда
её производная в этой точке существует
и конечна:
функцииfв точкеx0, будучи пределом,
может не существовать или существовать
и быть конечной или бесконечной. Функцияfявляется дифференцируемой в точкеx0тогда и только тогда, когда
её производная в этой точке существует
и конечна:
![]()
Для дифференцируемой в x0функцииfв окрестностиU(x0) справедливо представление
![]() при
при
![]()
18Правила дифференцирования
При
дифференцировании константу можно
выносить за производную:
![]() Правило
дифференцирования суммы функций:
Правило
дифференцирования суммы функций:
![]() Правило
дифференцирования разности функций:
Правило
дифференцирования разности функций:
![]() Правило
дифференцирования произведения функций
(правило Лейбница):
Правило
дифференцирования произведения функций
(правило Лейбница):
![]() Правило
дифференцирования частного функций:
Правило
дифференцирования частного функций:
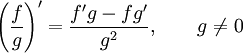 Правило
дифференцирования функции в степени
другой функции:
Правило
дифференцирования функции в степени
другой функции:
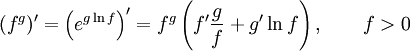 Правило
дифференцирования сложной функции:
Правило
дифференцирования сложной функции:
![]() Правило
логарифма при дифференцировании функции:
Правило
логарифма при дифференцировании функции:
![]()
19Производная обратной функции
Пусть
f
: [a,
b]
→ [c,
d]
непрерывная, строго монотонная на
интервале [a,
b]
функция, имеющая производную в точке
х0
![]() [a,
b].
Тогда обратная функция g
= f
-1:
[c,
d]
→[a,
b]
имеет производную в точке y0
= f(x0)
интервала [c,
d]
равную
[a,
b].
Тогда обратная функция g
= f
-1:
[c,
d]
→[a,
b]
имеет производную в точке y0
= f(x0)
интервала [c,
d]
равную
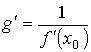 ,
,
если f '(x0) ≠ 0. Если f '(x0) = 0, то g '(y0) = + ∞ (в случае, когда f возрастает), и g '(y0) = − ∞ (в случае, когда f убывает). Доказательство. Пусть f (x) возрастает на [a, b] и f '(x) ≠ 0. Тогда в окрестности точки y0 = f (x0) существует обратная функция g = f -1; она непрерывна и также возрастает на [c, d], в силу чего g (y) ≠ g(y0), если у ≠ у0. Таким образом,
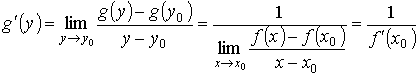
20Правило диференц. Сложн. Функ.
2. Правила дифференцированияарифметических дсйствий сложной функции.
Предположим, что f(x) и g(x) — две дифференцируемые функции в некотором промежутке.
Имеют место равенства (аргумент х опускаем):
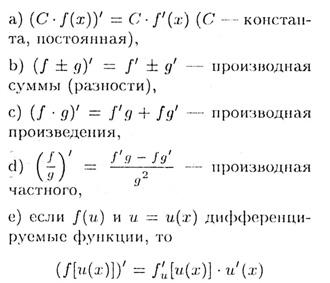
производная сложной функции.
Существование производной f'(x0) равносильно существованию касательной t к графику функции f(x) в точке A(x0,у0), где
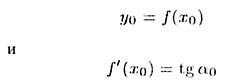
выражает ее угловой коэффициент. Уравнение t имеет вид
(t) : у = y0+ k(x - x0), k = f'(x0)
3. Если
S = S(t) —путь, пройденный материальной
точкой М за время
![]() t,
то
t,
то

- мгновенная скорость М в момент времени t.
