
- •1.Матрица.Транспонированная матрица.Сложение и умножение на число.
- •2Отрицательная матрица
- •3Элементарные преобразования матрицы.Вырожденные и невырожденные.
- •4 Минора и алгеброические дополнения
- •6 Обратная матрица
- •7Ранг матрицы
- •Связанные определения
- •8Системы линейных уравнений
- •9Система линейных уравнений решение методом гаусса
- •10Решение системы с помощью обратной матрицы
- •11Кривые второго порядка
- •12Окружность
- •13Элиппс
- •14Гипербола
- •15Парабола
- •17Дифференци́рованием.
- •[Править] Определение производной функции через предел
- •18Правила дифференцирования
- •19Производная обратной функции
- •20Правило диференц. Сложн. Функ.
- •21И22 на листке.
- •23Производные от обратных тригонометрических функций
- •24Дифференциал
- •25Производные и дифференциалы высших порядков
- •26Дифференцирование функций, заданных параметрически
- •27Теорема Ферма
- •28И29Теоремы Ролля, Лагранжа, Коши
- •30Тейлора формула
- •31Раскрытие неопределенностей. Правило Лопиталя
- •32Точки экстремума
- •Необходимое условие экстремума
- •Достаточное условие экстремума
- •Общий план исследования функции и построения графика.
- •35Неопределенный интеграл и его свойства. Таблица интегралов.
- •36Метод замены переменной (метод подстановки)
- •Интегрирование по частям
- •37Интегрирование рациональных выражений
- •38Эйлера подстановки
- •39Определения
- •41Определения
- •Стандартная модель
- •Матричная модель
- •Замечания
- •Модуль и аргумент
- •Сопряжённые числа
- •Алгебраическая форма
- •Тригонометрическая и показательная формы
- •42Геометрическая интерпретация комплексного числа
35Неопределенный интеграл и его свойства. Таблица интегралов.
Определение первообразной и неопределенного интеграла
Функция F(x) называется первообразной функции f(x), если
![]()
Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как
![]()
Таким образом, если F - некоторая частная первообразная, то справедливо выражение
![]()
где С - произвольная постоянная.
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины.
![]()
![]()
![]()
![]()
36Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличнымили к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть
требуется вычислить интеграл
![]() Сделаем
подстановку
Сделаем
подстановку![]() где
где![]() —
функция, имеющая непрерывнуюпроизводную.
—
функция, имеющая непрерывнуюпроизводную.
Тогда
![]() и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаемформулу интегрирования
подстановкой:
и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаемформулу интегрирования
подстановкой:
![]()
Интегрирование по частям
Основная статья: Интегрирование по частям
Интегрирование по частям — применение следующей формулы для интегрирования:
![]()
В частности, с помощью n-кратного применения этой формулы находится интеграл
![]()
где Pn + 1(x) — многочлен (n+ 1)-ой степени.
37Интегрирование рациональных выражений
Отношение двух алгебраических многочленов
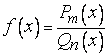 ,
(1)
,
(1)
![]() ,
,
![]() ,
,
![]() ,
называется рациональной функцией и еще
рациональной дробью.
,
называется рациональной функцией и еще
рациональной дробью.
Будем
считать, что рациональная дробь
![]() действительная,
т. е.
действительная,
т. е.![]() и
и![]() -
действительные многочлены. Кроме того,
будем считать, что
-
действительные многочлены. Кроме того,
будем считать, что![]() -
действительная переменная.
-
действительная переменная.
Рациональные функции вида
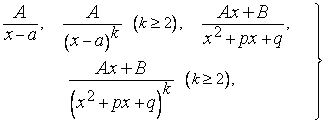 (2)
(2)
где
![]() ,
,![]() ,
,![]() ,
,![]() -
действительные числа,
-
действительные числа,![]() -
натуральное число, а трехчлен
-
натуральное число, а трехчлен![]() не
имеет действительных корней, будем
называть простейшими дробями.
не
имеет действительных корней, будем
называть простейшими дробями.
В § 5.2. мы показали, как вычисляются интегралы от простейших дробей (см. (4), (5), (6), (7), (11), § 5.2).
Пусть
надо найти неопределенный интеграл от
рациональной функции
![]() (см.
(1)). Если
(см.
(1)). Если![]() ,
то простым делением выделяем из
,
то простым делением выделяем из![]() целую
часть:
целую
часть:
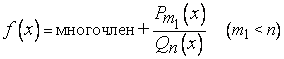 .
.
Интегрирование многочлена не представляет труда, и трудность свелась к интегрированию рациональной дроби, у которой степень числителя меньше степени знаменателя.
Будем
поэтому считать, что наша рациональная
дробь
![]() правильная,
т. е. степень ее числителя меньше степени
знаменателя
правильная,
т. е. степень ее числителя меньше степени
знаменателя![]() .
.
Т е о р е м а 2. Пусть знаменатель правильной действительной рациональной дроби разложен по формуле (5’) § 5.5:
![]() .
.
Тогда дробь (1) можно представить, и притом единственным образом, в виде следующей суммы простейших дробей:
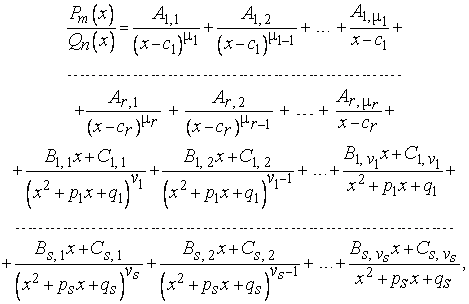 (3)
(3)
где
![]() ,
,![]() ,
,![]() (с
соответствующими индексами) – постоянные
числа.
(с
соответствующими индексами) – постоянные
числа.
Эта
теорема утверждает, что для любой
правильной рациональной действительной
дроби существуют постоянные числа
![]() ,
,![]() ,
,![]() с
указанными индексами так, что имеет
место тождество (3) для всех
с
указанными индексами так, что имеет
место тождество (3) для всех![]() ,
исключая значения
,
исключая значения![]() ,
для которых обе части (3) не определены.
Эту теорему можно аккуратно доказать,
но мы здесь ее доказывать не будем.
,
для которых обе части (3) не определены.
Эту теорему можно аккуратно доказать,
но мы здесь ее доказывать не будем.
Поясним формулировку теоремы 1 на примере. Согласно теореме 1 имеет место равенство
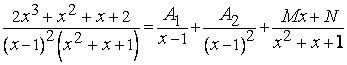 ,
(4)
,
(4)
где
![]() ,
,![]() ,
,![]() ,
,![]() -
вполне определенные постоянные числа.
Чтобы найти их, приводим (4) к общему
знаменателю и приравниваем числители
левой и правой частей:
-
вполне определенные постоянные числа.
Чтобы найти их, приводим (4) к общему
знаменателю и приравниваем числители
левой и правой частей:
![]()
![]() .
(5)
.
(5)
Раскрывая
скобки в правой части (5), группируем
члены с одинаковыми степенями
![]() и
приравниваем коэффициенты при одинаковых
степенях
и
приравниваем коэффициенты при одинаковых
степенях![]() обеих
частей (см. § 4.14, теорема 2);
обеих
частей (см. § 4.14, теорема 2);
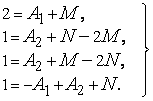 (6)
(6)
Мы
получили четыре линейных уравнения с
четырьмя неизвестными
![]() ,
,![]() ,
,![]() ,
,![]() .
Эта система по теореме 1 имеет решение
и притом единственное. Решая систему
(6) получим
.
Эта система по теореме 1 имеет решение
и притом единственное. Решая систему
(6) получим![]() ,
,![]() ,
,![]() ,
и потому
,
и потому
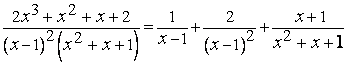 .
(7)
.
(7)
В общем
случае, если мы нашли коэффициенты
![]() в
(3), для интегрирования дроби
в
(3), для интегрирования дроби![]() у
нас все готово: неопределенный интеграл
от левой части (3) равен сумме неопределенных
интегралов от всех членов правой плюс
некоторая постоянная
у
нас все готово: неопределенный интеграл
от левой части (3) равен сумме неопределенных
интегралов от всех членов правой плюс
некоторая постоянная![]() .
Выше уже было отмечено, что интегралы
от любого из членов (3) мы умеем вычислять.
.
Выше уже было отмечено, что интегралы
от любого из членов (3) мы умеем вычислять.
В случае примера (7)
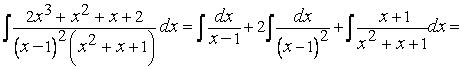
![]() .
.
З а м
е ч а н и е 1. Равенство (5) верно для
любого
![]() .
Но оно тогда верно и при
.
Но оно тогда верно и при![]() ,
потому что слева и справа в (5) стоят
непрерывные функции от
,
потому что слева и справа в (5) стоят
непрерывные функции от![]() .
Подставив в (5)
.
Подставив в (5)![]() ,
получим
,
получим![]() ,
т. е.
,
т. е.![]() и,
положив
и,
положив![]() ,
получим
,
получим![]() ,
т. е.
,
т. е.![]() .
Эти данные
.
Эти данные![]() сильно
упрощают систему (6). На практике подобными
соображениями не надо пренебрегать.
сильно
упрощают систему (6). На практике подобными
соображениями не надо пренебрегать.
З а м
е ч а н и е 2. Принципиально всякая
рациональная функция интегрируется в
элементарных функциях. Практически
полное интегрирование (1) можно довести
до конца в случае, если известны все
корни
![]() и
их кратности. Но мы уже говорили в § 5.5,
что это не всегда удается узнать. В связи
с этим всякого рода упрощения интеграла
от рациональной дроби (1) являются очень
ценными.
и
их кратности. Но мы уже говорили в § 5.5,
что это не всегда удается узнать. В связи
с этим всякого рода упрощения интеграла
от рациональной дроби (1) являются очень
ценными.
С этой точки зрения заслуживает большого внимания метод Остроградского, обычно излагаемый в более полных учебниках.
