
- •1.Матрица.Транспонированная матрица.Сложение и умножение на число.
- •2Отрицательная матрица
- •3Элементарные преобразования матрицы.Вырожденные и невырожденные.
- •4 Минора и алгеброические дополнения
- •6 Обратная матрица
- •7Ранг матрицы
- •Связанные определения
- •8Системы линейных уравнений
- •9Система линейных уравнений решение методом гаусса
- •10Решение системы с помощью обратной матрицы
- •11Кривые второго порядка
- •12Окружность
- •13Элиппс
- •14Гипербола
- •15Парабола
- •17Дифференци́рованием.
- •[Править] Определение производной функции через предел
- •18Правила дифференцирования
- •19Производная обратной функции
- •20Правило диференц. Сложн. Функ.
- •21И22 на листке.
- •23Производные от обратных тригонометрических функций
- •24Дифференциал
- •25Производные и дифференциалы высших порядков
- •26Дифференцирование функций, заданных параметрически
- •27Теорема Ферма
- •28И29Теоремы Ролля, Лагранжа, Коши
- •30Тейлора формула
- •31Раскрытие неопределенностей. Правило Лопиталя
- •32Точки экстремума
- •Необходимое условие экстремума
- •Достаточное условие экстремума
- •Общий план исследования функции и построения графика.
- •35Неопределенный интеграл и его свойства. Таблица интегралов.
- •36Метод замены переменной (метод подстановки)
- •Интегрирование по частям
- •37Интегрирование рациональных выражений
- •38Эйлера подстановки
- •39Определения
- •41Определения
- •Стандартная модель
- •Матричная модель
- •Замечания
- •Модуль и аргумент
- •Сопряжённые числа
- •Алгебраическая форма
- •Тригонометрическая и показательная формы
- •42Геометрическая интерпретация комплексного числа
8Системы линейных уравнений
Обозначим
через
![]() любое
из множеств
любое
из множеств
![]() или
или
![]() .
.
Системой
линейных уравнений(л.у.) над
![]() называется
совокупность (набор) из нескольких
уравнений от одного и того же набора
переменных (неизвестных)
называется
совокупность (набор) из нескольких
уравнений от одного и того же набора
переменных (неизвестных)
![]() :
:
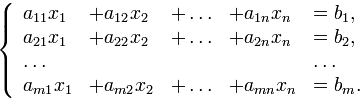
Здесь
числа
![]() и
и
![]() —
из
—
из
![]() ;
они называютсякоэффициентами
системы. Первый индекс у коэффициента
;
они называютсякоэффициентами
системы. Первый индекс у коэффициента
![]() отвечает
за номер уравнения, а второй — за номер
переменной. Относительно числа
отвечает
за номер уравнения, а второй — за номер
переменной. Относительно числа
![]() уравнений
не делается ни какого предположения:
оно может быть меньше, больше или равно
числу переменных
уравнений
не делается ни какого предположения:
оно может быть меньше, больше или равно
числу переменных
![]() .
Если
.
Если
![]() то
система называетсяпереопределенной.Решением системы уравненийназывается любой набор значений
переменных
то
система называетсяпереопределенной.Решением системы уравненийназывается любой набор значений
переменных
![]() ,
обращающий каждое из уравнений в истинное
равенство. Система называетсясовместнойесли она имеет хотя бы одно решение инесовместнойв противном
случае.
,
обращающий каждое из уравнений в истинное
равенство. Система называетсясовместнойесли она имеет хотя бы одно решение инесовместнойв противном
случае.
!
Можно доказать (см. результаты НИЖЕ), что все возможности для произвольной системы ограничиваются следующими вариантами:
1. система совместна и имеет единственное решение;
2. cистема совместна и имеет бесконечное множество решений;
3. cистема несовместна.
При
этом все решения будут находиться в том
же множестве
![]() ,
что и коэффициенты системы.
,
что и коэффициенты системы.
x
i = Di
(i =
![]() ). Формула
крамера
). Формула
крамера
9Система линейных уравнений решение методом гаусса
В
отличие от матричного
методаиметод
Крамера, метод Гаусса может
быть применен к системам линейных
уравнений с произвольным числом уравнений
и неизвестных. Суть метода заключается
в последовательном исключении
неизвестных.
Рассмотрим систему
линейных уравнений :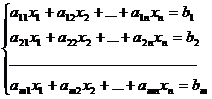
Разделим обе части 1–го уравнения на a11не равно 0, затем: 1) умножим на а21и вычтем из второго уравнения 2) умножим на а31и вычтем из третьего уравнения и т.д.
Получим:
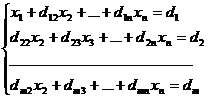 ,
гдеd1j = a1j/a11,
j = 2, 3, …, n+1.
,
гдеd1j = a1j/a11,
j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Пример:Решить систему линейных
уравнений методом Гаусса.
Составим расширенную матрицу системы.
А* =
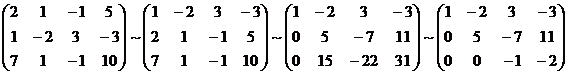
Таким образом, исходная система может быть представлена в виде:
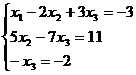 ,
откуда получаем: x3= 2; x2= 5; x1= 1.
,
откуда получаем: x3= 2; x2= 5; x1= 1.
Пример.Решить систему методом Гаусса.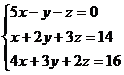
Для решения методом гаусса уравнения, составим расширенную матрицу системы.
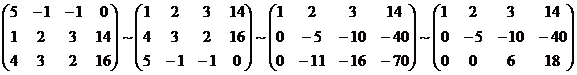 Таким
образом, исходная система может быть
представлена в виде:
Таким
образом, исходная система может быть
представлена в виде:
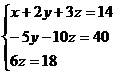 ,
откуда получаем: z = 3; y = 2; x = 1.
Полученный
ответ совпадает с ответом, полученным
для данной системы методом Крамера и
матричным методом.
,
откуда получаем: z = 3; y = 2; x = 1.
Полученный
ответ совпадает с ответом, полученным
для данной системы методом Крамера и
матричным методом.
Для
самостоятельного решения:
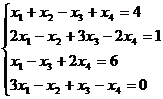 Ответ: {1, 2, 3, 4}.
Ответ: {1, 2, 3, 4}.
10Решение системы с помощью обратной матрицы
Решить
систему с матричным методом
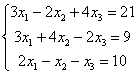
Решение:
Запишем систему в матричной форме:
![]() ,
где
,
где
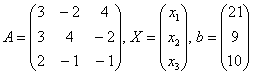
Единственный комментарий: если бы в
уравнениях отсутствовали некоторые
переменные, то на соответствующих местах
в матрице
![]() нужно
было бы поставить нули.
нужно
было бы поставить нули.
Обратную
матрицу найдем по формуле![]() .
.
Согласно
формуле нам нужно найти обратную матрицу
![]() и
выполнить матричное умножение
и
выполнить матричное умножение
![]() .
Обратную матрицу найдем по формуле:
.
Обратную матрицу найдем по формуле:![]() ,
где
,
где
![]() –
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
![]() .
.
Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.
Внимание!
Если
![]() ,
то обратной матрицы не существует, и
решить систему матричным методом
невозможно. В этом случае система
решается методом
исключение неизвестных (методом Гаусса).
,
то обратной матрицы не существует, и
решить систему матричным методом
невозможно. В этом случае система
решается методом
исключение неизвестных (методом Гаусса).
Теперь
нужно вычислить 9 миноров и записать их
в матрицу миноров
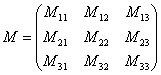
Справка:Полезно знать смысл двойных подстрочных
индексов в линейной алгебре. Первая
цифра – это номер строки, в которой
находится данный элемент. Вторая цифра
– это номер столбца, в котором находится
данный элемент: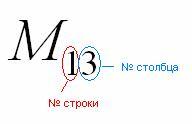 То
есть, двойной подстрочный индекс
указывает, что элемент
То
есть, двойной подстрочный индекс
указывает, что элемент
![]() находится
в первой строке, третьем столбце, а,
например, элемент
находится
в первой строке, третьем столбце, а,
например, элемент
![]() находится
в 3 строке, 2 столбце
находится
в 3 строке, 2 столбце
В ходе
решения расчет миноров лучше расписать
подробно, хотя, при определенном опыте
их можно приноровиться считать с
ошибкамиустно.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом:
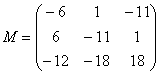 –
матрица миноров соответствующих
элементов матрицы
–
матрица миноров соответствующих
элементов матрицы
![]() .
.
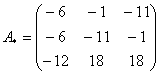 –
матрица алгебраических дополнений.
–
матрица алгебраических дополнений.
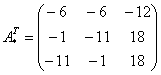 –
транспонированная матрица алгебраических
дополнений.
–
транспонированная матрица алгебраических
дополнений.
Теперь
записываем обратную матрицу:
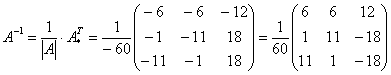
Ни
в коем случае не вносим
![]() в
матрицу, это серьезно затруднит дальнейшие
вычисления. Деление нужно было бы
выполнить, если бы все числа матрицы
делились на 60 без остатка. А вот внести
минус в матрицу в данном случае очень
даже нужно, это, наоборот – упростит
дальнейшие вычисления.
в
матрицу, это серьезно затруднит дальнейшие
вычисления. Деление нужно было бы
выполнить, если бы все числа матрицы
делились на 60 без остатка. А вот внести
минус в матрицу в данном случае очень
даже нужно, это, наоборот – упростит
дальнейшие вычисления.
Осталось провести матричное умножение. Умножать матрицы можно научиться на уроке Действия с матрицами. Кстати, там разобран точно такой же пример.
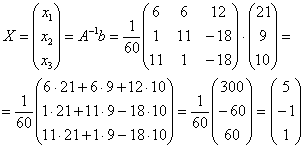
Обратите внимание, что деление на 60 выполняется в последнюю очередь. Иногда может и не разделиться нацело, т.е. могут получиться «плохие» дроби. Что в таких случаях делать, я уже рассказал, когда мы разбирали правило Крамера.
Ответ:
![]()
