26Дифференцирование функций, заданных параметрически

Пусть даны два уравнения

x=x(t),y=y(t), где t  [T1, T2].

(1)

Каждому значению tиз [T₁, T₂] соответствуют определенные значенияxиy. Если рассматривать значенияxиyкак координаты точки на плоскостиxOy, то каждому значениюtбудет соответствовать определенная точка плоскости. Когдаtизменяется от T₁до T₂, эта точка на плоскости описывает некоторую кривую. Уравнения (1) называютсяпараметрическими уравнениямиэтой кривой,tназываетсяпараметром, а способ задания кривой уравнениями (1) называетсяпараметрическим.

Предположим, что функция x=x(t)имеет обратнуюt=t(x). Тогда, очевидно, у является функцией отx: y=y[t(x)]. Следовательно, уравнения (1) определяютyкак функцию отx, и говорят, что функцияyотxзадаетсяпараметрически.

При рассмотрении функций, заданных параметрически, исключение параметра не всегда возможно. Во многих случаях удобнее задавать различные значения tи затем вычислять соответствующие значения аргументаxи функцииy.

Пример.Пусть кривая задана параметрическими уравнениями:

Построим эту кривую на плоскости, придавая различные значения параметру tи находя соответствующие значенияхиу.

При t =0 M(R, 0).

Таким образом, получаем окружность с центром в начале координат, радиуса R. Здесьtобозначает угол, образованный радиусом, проведенным в некоторую точку окружностиМ(x, y), и осьюOx.

Если исключим из этих уравнений параметр t, то получим уравнение окружности, содержащее толькоxиy. Возводя в квадрат параметрические уравнения и складывая их, находим:

x²+ y²=R²(cos²t + sin²t) или x²+ y²=R².

Выведем правило нахождения производных функций, заданных параметрически. Пусть x=x(t), y=y(t), причем на некотором отрезке [T₁, T₂] функцииx(t)иy(t)дифференцируемы иx' ≠ 0.

Т.к. у– функция, зависящая от переменнойx, то будем считать, что функцияx=x(t)имеет обратнуюt=t(x).

Будем обозначать: y_x' – производная функции по переменнойx, y_t', x_t', t_x' – соответственно производные поtих.

Воспользовавшись правилом дифференцирования сложной функции, получим . Производную t_x' найдем по правилу дифференцирования обратной функции .

Окончательно, .

Итак,

Полученную функцию можно рассматривать как функцию, заданную параметрически: .

Используя эту формулу, можно находить и производные высших порядков функций, заданных параметрически. Найдем . По определению второй производной . Учитывая, чтоy_x' есть функция параметраt,y_x'=f(t),получаем:

Примеры.

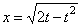1. , y = arcsin (t–1). Найдем .

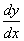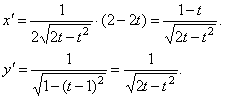
Следовательно, .

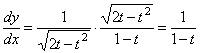2. Найти угловой коэффициент касательной к циклоиде x = a·(t – sin t), y = a·(1 – cost)

в произвольной точке (0 ≤t≤ 2·π).

Угловой коэффициент касательной .

x' =a·(1 – cost) ,y' =a·sint.Поэтому .

3. 

Найти .

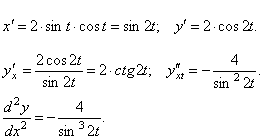
27Теорема Ферма

     Теорема Ферма, - утверждение, что для любого натурального числаn> 2 уравнениеxⁿ+yⁿ=zⁿ(уравнение Ферма) не имеет решений в целых ненулевых числахx,y,z. Теорема была сформулирована Пьером Ферма примерно в 1630 году на полях книги Диофанта "Арифметика" следующим образом: "невозможно разложить ни куб на два куба, ни биквадрат на два биквадрата, и вообще никакую степень, большую квадрата, на две степени с тем же показателем". И далее добавил: "я открыл этому поистине чудесное доказательство, но эти поля для него слишком малы". В бумагах Пьера Ферма нашли доказательство теоремы Ферма дляn= 4. Нездоровый интерес к доказательству этой теоремы среди неспециалистов в области математики был в свое время вызван большой международной премией, аннулированной в конце первой мировой войны.

     Предполагается, что доказательство теоремы Ферма вообще не существовало.

     Для n= 3 теорему Ферма доказал Л. Эйлер, дляn= 5 И. Дирихле и А. Лежандр, дляn= 7 - Г. Ламе. Теорему Ферма достаточно доказать для любого простого показателяn=p> 2, т. е. достаточно доказать, что уравнение

x^p+y^p=z^p(1)

не имеет решений в целых ненулевых взаимно простых числах x,y,z. Можно также считать, что числаxиyвзаимно просты сp. При доказательстве теоремы Ферма рассматривают два случая:первый случай, когда (xyz,p) = 1 ивторой случай, когдаp|z. Доказательство второго случая теоремы Ферма более сложно и обычно проводится методом бесконечного спуска. Существенный вклад в доказательство теоремы Ферма внес Э. Куммер, который создал принципиально новый метод, основанный на разработанной им арифметической теории кругового поля. Используется тот факт, что в поле , левая часть уравнения (1) разлагается на линейные множители , которые являютсяp-ми степенями идеальных чисел поля в первом случае и отличаются отp-х степеней на множитель во втором случае. Еслиpделит числители Бернулли чиселB_2n(n= 1, 2, ..., (p- 3)/2), то по критерию регулярностиpне делит числоhклассов идеалов поля и эти идеальные числа - главные. В этом случае Э. Куммер доказал теорему Ферма. Не известно бесконечно или конечно число регулярных чиселp(по теореме Иенсена число иррегулярных простых чисел бесконечно). Э. Куммер доказал теорему Ферма для некоторых классов иррегулярных простых чисел и тем самым установил ее справедливость для всехp< 100. В первом случае он показал, что из (1) следует выполнимость сравнений

n= 2, 4, ...,p- 3,

справедливых при любой перестановке x,y, -z. Отсюда он получил, что если в первом случае уравнение (1) разрешимо, то дляn= 3, 5

(2)