28И29Теоремы Ролля, Лагранжа, Коши

Теорема Ролля

Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f(a) = f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что f'(ξ) = 0.

Теорема Лагранжа

Если функция f: [a, b] → R непрерывна на сегменте [a, b] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то такое, что f(b) - f(a) = f'(ξ)(b - a).

Теорема Коши

Если каждая из функций f и g непрерывна на [a, b] и имеет конечную или бесконечную производную на ]a, b[ и если, кроме того, производная g'(x) ≠ 0 на ]a, b[, то такое, что справедлива формула

Если дополнительно потребовать, чтобы g(a) ≠ g(b), то условие g'(x) ≠ 0 можно заменить менее жестким:

30Тейлора формула

Тейлора формула

        формула

        

        

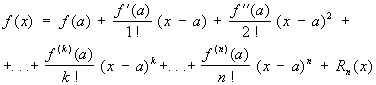
        изображающая функцию f (x), имеющую n-ю производную f ⁽ⁿ⁾(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена R_n (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) ⁿ [то есть R_n (x) = an (x)(x—a) ⁿ, где an (x) → 0 при х → а]. Если в интервале между а и х существует (n + 1)-я производная, то R_n (x) можно представить в видах:

        

        ,

        где ξ и ξ₁ — какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а Соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.

31Раскрытие неопределенностей. Правило Лопиталя

1. Неопределенность вида 0/0. Первое правило Лопиталя.

Если = 0, то , когда последний существует.

2. Неопределенность вида ¥/. Второе правило Лопиталя.

Если = ¥, то , когда последний существует.

3. Неопределенности вида 0× ,  - , 1^ и 0⁰ сводятся к неопределенностям 0/0 и ¥/ путем алгебраических преобразований.

Пример 3.25.Найти предел функции y =при x  0.

Решение. Имеем неопределенность вида -. Сначала преобразуем ее к неопределенности вида 0/0, для чего достаточно привести дроби к общему знаменателю. К полученному выражению два раза применим правило Лопиталя. Записывая последовательно все промежуточные вычисления, будем иметь:

= = == ==.

Пример 3.26. Найти .

Решение. Раскрывая неопределенность вида / по правилу Лопиталя, получаем:

= = =0.

Пример 3.27. Вычислить .

Решение. Имеем неопределенность вида 1^. Обозначим искомый предел через A. A = .

Тогда lnA= = = = 2, 

32Точки экстремума

   Точка x₀ называется точкой строгого локального максимума (минимума) функции f (x), если для всех значений аргумента из некоторой достаточно малой δ - окрестности точки х₀ выполняется неравенство

f (x) < f (x₀) ( f ( x) > f ( x₀ ) )

при х ≠ x₀.    Локальный максимум и локальный минимум объединяются общим названием экстремум. Из определения следует, что понятие экстремума носит локальный характер в том смысле, что неравенство f ( x) < f ( x₀) ( f (x) > f ( x₀ )) может и не выполняться для всех значений х в области определения функции, а должно выполняться лишь в некоторой окрестности точки x₀.    Очевидно, функция может иметь несколько локальных максимумов и несколько локальных минимумов, причем может так случиться, что иной локальный максимум окажется меньше какого-то другого локального минимума.    В точках экстремума приращение функции имеет определённый знак. Если Δ f = f ( x₀ + h ) − f ( x₀) ≥ 0 для достаточно малых значений h, то точка х₀ является точкой локального минимума. Если Δ f = f ( x₀ + h ) − f (x₀) ≤ 0 для достаточно малых значений h, то точка х₀ является точкой локального максимума. Точки экстремума это точки графика функции, которые отделяют участки определённой монотонности друг от друга.    Ниже приведены виды точек экстремумов. В первых двух функция определена и производная существует, такие точки называются стационарными.     Функция в точках экстремума определена, однако производной в точке экстремума может не существовать.