Необходимое условие экстремума

   Теорема. Если х₀ — точка экстремума функции f (x), то либо в этой точке производная обращается в нуль f ' (x₀) = 0 (в стационарных точках), либо в этих точках производная не существует (в угловых точках).    Доказательство. Рассмотрим разложение функции в окрестности точки х₀ в ряд Тейлора с остаточным членом в форме Пеано

Δ f (x) = f ' (x₀)·Δ x + o(Δ x).

Так как остаточный член является бесконечно малой величиной относительно приращения аргумента, то

sign Δ f (x) = sign f ' (x₀)·sign Δ x,

и знак приращения функции зависит от знака приращения аргумента sign (Δ x). Что недопустимо для точек экстремума. Следовательно производная функции в точке х₀ или равна нулю, или не должна существовать.

Достаточное условие экстремума

   Теорема. Пусть функция f (x) непрерывна в некотором интервале, содержащую точку экстремума х₁, и дифференцируема во всех точках этого интервала кроме, быть может самой точки х₁. Если при переходе слева направо через эту точку х₁ производная меняет знак с плюса на минус, то при х = х₁ функция имеет локальный максимум. Если же при переходе слева направо через эту точку х₁ производная меняет знак с минуса на плюс, то функция имеет в этой точке локальный минимум.    Комментарий. Если в достаточно малой окрестности точки х₁ справедливо f ' (x) > 0 при х < x₁, f ' (x) < 0 при х > x₁, то в точке х₁ функция имеет максимум; если f ' (x) < 0 при х < x₁, f ' (x) > 0 при х > x₁, то в точке х₁ функция имеет минимум.    Доказательство. Пусть при переходе слева направо через эту точку х₁ производная меняет знак с плюса на минус, то есть для всех х, достаточно близких к х₁, имеем f ' (x) > 0 при х < x₁, f ' (x) < 0 при х > x₁. Применяя теорему Лагранжа к разности f (x) − f ( x₁), получим

f ( x ) − f ( x₁ ) = f ' ( c )·( x − x₁ ).

где с лежит между точками х и х₁. По условию теоремы

sign f ' ( c ) = − sign ( x − x₁ ),

поэтому в произвольно малой окрестности точки х₁ имеем

f ( x ) < f ( x₁ ).

В этом случае точка х₁ есть точка локального максимума, что и требовалось доказать

Общий план исследования функции и построения графика.

1) Отыскивается область определения функции.Исследование функции начинают с поиска области определения. Под областью определения понимается множество всех значений аргумента, при которых функция определена, то есть может быть вычислена. При нахождении области определения функции следует обращать внимание на выражения содержащие дроби, так как, знаменатель дроби не может обращаться в нуль. Следует обращать внимание на корни, так как, подкоренное выражение должно быть неотрицательным. Особое внимание следует обратить на логарифмы, входящие в выражение. Если функция содержит логарифм     , то на область определения накладываются ограничения исходя из неравенств

.

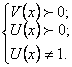2) Исследуем общие свойства функции: чётность; нечётность; периодичность. Функция     называется чётной, если. График чётной функции симметричен относительно оси ординат. Например, функция- чётная, так как. Функция называется нечётной, если.График функции симметричен относительно начала координат (центральная симметрия). Для примера рассмотрим функцию     . Она нечётная, так как. Если функция ни чётная, ни нечётная, то говорят, что функция имеет график общего положения. Если существуеттакое, что для любоговыполняется условие, то функцияназывается периодической. Наименьшее из чисел, удовлетворяющих указанному условию, называют периодом. График периодической функции строят так. Сначала строят график на одном периоде, а потом копируют построенный участок вдоль всей оси. Запись периодические функции, как правило, содержит тригонометрические функции синуса, косинуса, тангенса и котангенса.

3) Находим точки пересечения графика функции с осями координат. Абсцисса пересечение с осью     ищется исходя из уравнения. Ордината пересечение с осьюищется подстановкой значенияв выражение функцииЕсли пересечение с осьюнайти не удаётся, то обходятся без него. Обычно поиск пересечения с осьюне представляет труда.4) Исследуется непрерывность функции, находятся точки разрыва. Функция     называется непрерывной в точке, если она определена в этой точке и существует предел, который равен значению функции. То есть

.

Функция называется непрерывной на промежутке (отрезке), если она непрерывна в каждой точке этого промежутка (отрезка). График непрерывной функции может быть изображён без отрыва карандаша (мела, пера, ручки,…). Точка     является точкой разрыва функции, если функция определена и непрерывна в окрестности точки, а в самой точке не является непрерывной (хотя может быть определённой). В этом случае говорят, что функция терпит разрыв в точке. Выделяют три типа точек разрыва: устранимый разрыв; конечный разрыв (разрыв первого рода); бесконечный разрыв (разрыв второго рода).

5) Ищутся асимптоты графика функции.

Прямая называется асимптотой графика функции, если расстояние от точек графика до этой прямой стремится к нулю при бесконечном удалении от начала координат вдоль графика функции. Образно выражаясь, график как бы прилипает к асимптоте. Асимптоты бывают вертикальные, наклонные и горизонтальные. Вертикальные асимптоты ищутся по точкам разрыва второго рода. Если в точке     функция терпит бесконечный разрыв, то вертикальная прямаяявляется вертикальной асимптотой. Например, в точкефункцияимеет разрыв второго рода. Следовательно, уравнение вертикальной асимптоты. График функции имеет наклонную асимптоту при(соответственно при), если существуют конечные пределы(соответственно). При этом уравнение наклонной асимптоты. Если хотя бы один из двух пределов не существует (или бесконечен), то соответствующей наклонной асимптоты нет. Еслии существует конечный предел, то асимптота является горизонтальной и её уравнение.

6) Находятся критические точки и интервалы монотонности. Функция     имеет максимум в точке, если её значение в этой точке больше, чем её значения во всех точках некоторой окрестности, содержащей точку. Функцияимеет минимум в точке, если её значение в этой точке меньше, чем её значения во всех точках некоторой окрестности, содержащей точку. Для определения критических точек находим производную по соответствующим правилам и используя таблицу производных. В критических точках производная равна нулю или не существует. Определяем знак производной в интервалах между критическими точками. Если на некотором интервале производная положительна, то функция возрастает. Если производная отрицательна, то на данном интервале функция убывает.

7) Ищутся точки перегиба и интервалы выпуклости.

Для определения точек перегиба находят вторую производную. В точке перегиба вторая производная равна нулю или не существует. По знаку второй производной в интервалах между точками перегиба определяют направление выпуклости графика функции. Если вторая производная положительна, то график функции выпуклый вниз. Если вторая производная отрицательная, то график функции выпуклый вверх. 8)

На основании проведённого исследования строим график.

Если необходимо вычисляем значение функции в некоторых промежуточных точках.

34ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Функция F (х) называется первообразной функцией для  данной функции f (х) (или, короче, первообразной данной функции f (х)) на данном промежутке, если на этом промежутке .Пример. Функция является  первообразной функциина всей числовой оси, так какпри любомх. Отметим, что вместе с  функцией первообразной дляявляется любая функция вида, гдеС —  произвольное постоянное число (это следует из того, что производная постоянной равна нулю). Это свойство имеет место и в общем случае.

Теорема 1. Если и— две  первообразные для функцииf (х) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу. Из этой теоремы следует, что если известна какая-нибудь первообразная F (х) данной  функции f (х), то все множество первообразных для f (х) исчерпывается функциями F (х) + С. Выражение F (х) + С, где F (х) —  первообразная функции f (х) и С — произвольная  постоянная, называется неопределенным интегралом от функции f (х) и обозначается символом , причемf (х) называется подынтегральной функцией ; —подынтегральным выражением, х — переменной  интегрирования; ∫ — знак неопределенного интеграла. Таким образом, по определению если. Возникает вопрос:для всякой ли функции f (х) существует первообразная, а значит, и  неопределенный интеграл? Теорема 2. Если функция f (х) непрерывна на [a ; b], то на этом отрезке для функции f (х) существует первообразная. Ниже мы будем говорить о первообразных лишь для непрерывных функций. Поэтому  рассматриваемые нами далее в этом параграфе  интегралы существуют.