
- •1.Матрица.Транспонированная матрица.Сложение и умножение на число.
- •2Отрицательная матрица
- •3Элементарные преобразования матрицы.Вырожденные и невырожденные.
- •4 Минора и алгеброические дополнения
- •6 Обратная матрица
- •7Ранг матрицы
- •Связанные определения
- •8Системы линейных уравнений
- •9Система линейных уравнений решение методом гаусса
- •10Решение системы с помощью обратной матрицы
- •11Кривые второго порядка
- •12Окружность
- •13Элиппс
- •14Гипербола
- •15Парабола
- •17Дифференци́рованием.
- •[Править] Определение производной функции через предел
- •18Правила дифференцирования
- •19Производная обратной функции
- •20Правило диференц. Сложн. Функ.
- •21И22 на листке.
- •23Производные от обратных тригонометрических функций
- •24Дифференциал
- •25Производные и дифференциалы высших порядков
- •26Дифференцирование функций, заданных параметрически
- •27Теорема Ферма
- •28И29Теоремы Ролля, Лагранжа, Коши
- •30Тейлора формула
- •31Раскрытие неопределенностей. Правило Лопиталя
- •32Точки экстремума
- •Необходимое условие экстремума
- •Достаточное условие экстремума
- •Общий план исследования функции и построения графика.
- •35Неопределенный интеграл и его свойства. Таблица интегралов.
- •36Метод замены переменной (метод подстановки)
- •Интегрирование по частям
- •37Интегрирование рациональных выражений
- •38Эйлера подстановки
- •39Определения
- •41Определения
- •Стандартная модель
- •Матричная модель
- •Замечания
- •Модуль и аргумент
- •Сопряжённые числа
- •Алгебраическая форма
- •Тригонометрическая и показательная формы
- •42Геометрическая интерпретация комплексного числа
41Определения
Поле
комплексных чисел можно понимать как
расширение
полявещественных чисел, в
котором многочленz2+ 1 имеет
корень. Следующие две элементарныемоделипоказывают, что непротиворечивое
построение такой системы чисел возможно.
Оба приведенных определения приводят
кизоморфнымрасширениям поля вещественных чисел![]() ,
как и любые другие конструкцииполя
разложениямногочленаz2+ 1.
,
как и любые другие конструкцииполя
разложениямногочленаz2+ 1.
Стандартная модель
Комплексное число zможно определить как упорядоченную парувещественных чисел(x,y). Введём операции сложения и умножения таких пар следующим образом:
Вещественные
числа являются в этой модели подмножеством
множества комплексных чисел и представлены
парами вида
![]() ,
причём операции с такими парами
согласованы с обычными сложением и
умножением вещественных чисел. Ноль
представляется парой
,
причём операции с такими парами
согласованы с обычными сложением и
умножением вещественных чисел. Ноль
представляется парой![]() единица
—
единица
—![]() амнимая
единица—
амнимая
единица—![]() На
множестве комплексных чисел ноль и
единица обладают теми же свойствами,
что и на множестве вещественных, а
квадрат мнимой единицы, как легко
проверить, равен
На
множестве комплексных чисел ноль и
единица обладают теми же свойствами,
что и на множестве вещественных, а
квадрат мнимой единицы, как легко
проверить, равен![]() ,
то есть − 1.
,
то есть − 1.
Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные сотношением порядка(больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа так, чтобы операции по-прежнему были согласованы с порядком, невозможно.
Матричная модель
Комплексные числа можно также определить как семейство вещественных матрицвида
![]()
с обычным матричным сложением и умножением. Действительной единице будет соответствовать
![]()
мнимой единице —
![]()
Замечания
Ошибочно определение числа iкак единственного числа, удовлетворяющего уравнениюx2= − 1, так как число ( −i) также удовлетворяет этому уравнению.
Следует
также заметить, что выражение
![]() ,
ранее часто использовавшееся вместоi, не вполне корректно, так как
алгебраический корень определяется
над множеством неотрицательных чисел.
Вплоть до XIX века включительно запись
вроде
,
ранее часто использовавшееся вместоi, не вполне корректно, так как
алгебраический корень определяется
над множеством неотрицательных чисел.
Вплоть до XIX века включительно запись
вроде![]() считалась
допустимой, но в настоящее время, во
избежание ошибок, принято записывать
это выражение как
считалась
допустимой, но в настоящее время, во
избежание ошибок, принято записывать
это выражение как![]() .
Пример возможной ошибки при неосторожном
использовании устаревшей записи:
.
Пример возможной ошибки при неосторожном
использовании устаревшей записи:
![]()
в то время как правильный ответ:
![]()
Сравнение
a + bi = c + di означает, что a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение
(a + bi) + (c + di) = (a + c) + (b + d)i.
Вычитание
(a + bi) − (c + di) = (a − c) + (b − d)i.
Умножение
![]()
Деление
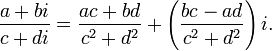

![]()
Геометрическое представление комплексного числа
Рассмотрим
плоскость с прямоугольной
системой координат. Каждому
комплексному числу![]() сопоставим
точку плоскости с координатами {x,y}
(а такжерадиус-вектор,
соединяющий начало координат с этой
точкой). Такая плоскость называетсякомплексной.
Вещественные числа на ней занимают
горизонтальную ось, мнимая единица
изображается единицей на вертикальной
оси; по этой причине горизонтальная и
вертикальная оси называются соответственновещественнойимнимойосями.
сопоставим
точку плоскости с координатами {x,y}
(а такжерадиус-вектор,
соединяющий начало координат с этой
точкой). Такая плоскость называетсякомплексной.
Вещественные числа на ней занимают
горизонтальную ось, мнимая единица
изображается единицей на вертикальной
оси; по этой причине горизонтальная и
вертикальная оси называются соответственновещественнойимнимойосями.
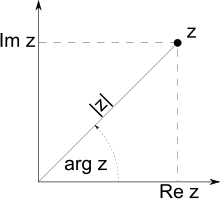
Часто бывает удобно рассматривать на комплексной плоскости также полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и уголрадиус-вектораточки (показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент). Подробнее см. ниже.
В этом наглядном представлении сумма комплексных чисел соответствует векторной суммесоответствующих радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него геометрически означает поворот радиус-вектора первого числа на угол, равный аргументу второго числа. Этот факт объясняет широкое использование комплексного представления втеории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза».
Геометрическая модель комплексных чисел широко используется в планиметрии: многие планиметрические теоремы можно доказать как некоторые комплексные тождества. Некоторые планиметрические утверждения (например, теорема Клиффорда), допускают только доказательство при помощи счёта в комплексных координатах.
![]()
Модуль, аргумент, вещественная и мнимая части
Пусть
![]() —
комплексное число, где
—
комплексное число, где![]() и
и![]() —вещественные
числа. Числа
—вещественные
числа. Числа![]() или
или![]() и
и![]() или
или![]() называются
соответственновещественнойимнимой(аналогичноангл.real,
imaginary) частямиz.
называются
соответственновещественнойимнимой(аналогичноангл.real,
imaginary) частямиz.
Если x = 0, то z называется мнимым или чисто мнимым числом.
Если y = 0, то z является действительным (вещественным) числом.
