
- •1.Матрица.Транспонированная матрица.Сложение и умножение на число.
- •2Отрицательная матрица
- •3Элементарные преобразования матрицы.Вырожденные и невырожденные.
- •4 Минора и алгеброические дополнения
- •6 Обратная матрица
- •7Ранг матрицы
- •Связанные определения
- •8Системы линейных уравнений
- •9Система линейных уравнений решение методом гаусса
- •10Решение системы с помощью обратной матрицы
- •11Кривые второго порядка
- •12Окружность
- •13Элиппс
- •14Гипербола
- •15Парабола
- •17Дифференци́рованием.
- •[Править] Определение производной функции через предел
- •18Правила дифференцирования
- •19Производная обратной функции
- •20Правило диференц. Сложн. Функ.
- •21И22 на листке.
- •23Производные от обратных тригонометрических функций
- •24Дифференциал
- •25Производные и дифференциалы высших порядков
- •26Дифференцирование функций, заданных параметрически
- •27Теорема Ферма
- •28И29Теоремы Ролля, Лагранжа, Коши
- •30Тейлора формула
- •31Раскрытие неопределенностей. Правило Лопиталя
- •32Точки экстремума
- •Необходимое условие экстремума
- •Достаточное условие экстремума
- •Общий план исследования функции и построения графика.
- •35Неопределенный интеграл и его свойства. Таблица интегралов.
- •36Метод замены переменной (метод подстановки)
- •Интегрирование по частям
- •37Интегрирование рациональных выражений
- •38Эйлера подстановки
- •39Определения
- •41Определения
- •Стандартная модель
- •Матричная модель
- •Замечания
- •Модуль и аргумент
- •Сопряжённые числа
- •Алгебраическая форма
- •Тригонометрическая и показательная формы
- •42Геометрическая интерпретация комплексного числа
Модуль и аргумент
Модулем (абсолютной величиной) комплексного числа называется длина радиус-векторасоответствующей точкикомплексной плоскости(или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль
комплексного числа zобозначается
|z| и определяется выражением![]() .
Часто обозначается буквами
.
Часто обозначается буквами![]() или
или![]() .
Еслиzявляетсявещественным
числом, то |z| совпадает сабсолютной
величинойэтого вещественного
числа.
.
Еслиzявляетсявещественным
числом, то |z| совпадает сабсолютной
величинойэтого вещественного
числа.
Для
любых
![]() имеют
место следующие свойства модуля. :
имеют
место следующие свойства модуля. :
1)
![]() ,
причём
,
причём![]() тогда
и только тогда, когда
тогда
и только тогда, когда![]() ;;
;;
2)
![]() (неравенство
треугольника);
(неравенство
треугольника);
3)
![]() ;
;
4)
![]() .
.
Из
третьего свойства следует
![]() ,
где
,
где![]() .
Данное свойство модуля вместе с первыми
двумя свойствами вводят на множестве
комплексных чисел структуру двумерногонормированного
пространстванад полем
.
Данное свойство модуля вместе с первыми
двумя свойствами вводят на множестве
комплексных чисел структуру двумерногонормированного
пространстванад полем![]() .
.
5) Для пары комплексных чисел z1 и z2 модуль их разности | z1 − z2 | равен расстоянию между соответствующими точками комплексной плоскости.
Угол
![]() (в
радианах)радиус-вектораточки, соответствующей числуz,
называетсяаргументомчислаzи обозначается
(в
радианах)радиус-вектораточки, соответствующей числуz,
называетсяаргументомчислаzи обозначается![]() .
.
Из этого определения следует, что
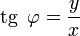 ;
;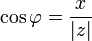 ;
;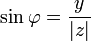 .
.Для комплексного нуля значение аргумента не определено, для ненулевого числа z аргумент определяется с точностью до 2kπ, где k — любое целое число.
Главным значением аргумента называется такое значение
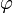 ,
что
,
что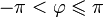 .
Часто главное значение обозначается
.
Часто главное значение обозначается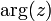 [4].
Главное значение аргумента обратного
числа отличается знаком от аргумента
исходного:
[4].
Главное значение аргумента обратного
числа отличается знаком от аргумента
исходного:
 .
.
Сопряжённые числа
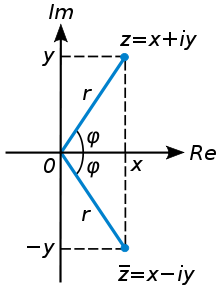
![]()
Геометрическое представление сопряжённых чисел
Если
комплексное число z=x+iy, то
число![]() называетсясопряжённым(или комплексно
сопряжённым) кz(обозначается такжеz*). На комплексной плоскости
сопряжённые числа получаются зеркальным
отражением друг друга относительно
вещественной оси. Модуль сопряжённого
числа такой же, как у исходного, а их
аргументы отличаются знаком.
называетсясопряжённым(или комплексно
сопряжённым) кz(обозначается такжеz*). На комплексной плоскости
сопряжённые числа получаются зеркальным
отражением друг друга относительно
вещественной оси. Модуль сопряжённого
числа такой же, как у исходного, а их
аргументы отличаются знаком.
Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.
 (сопряжённое
к сопряжённому есть исходное).
(сопряжённое
к сопряжённому есть исходное).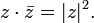

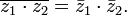
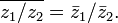
Обобщение:
![]() ,
гдеp(z) — произвольный многочлен
с вещественными коэффициентами.
,
гдеp(z) — произвольный многочлен
с вещественными коэффициентами.
Алгебраическая форма
Запись
комплексного числа zв видеx+iy,![]() ,
называетсяалгебраической формойкомплексного числа.
,
называетсяалгебраической формойкомплексного числа.
Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что i2= − 1):
(a + ib) + (c + id) = (a + c) + i(b + d);
![]()
Тригонометрическая и показательная формы
Если
вещественную xи мнимуюyчасти
комплексного числа выразить через
модульr= |z| и аргумент![]() (x=rcos φ,y=rsin φ), то всякое
комплексное числоz, кроме нуля,
можно записать втригонометрической
форме
(x=rcos φ,y=rsin φ), то всякое
комплексное числоz, кроме нуля,
можно записать втригонометрической
форме
z = r(cos φ + isin φ).
Также может быть полезна показательнаяформа записи комплексных чисел, тесно связанная с тригонометрической черезформулу Эйлера:
z = reiφ,
где eiφ— расширениеэкспонентыдля случая комплексного показателя степени.
Отсюда вытекают следующие широко используемые равенства:
![]()
42Геометрическая интерпретация комплексного числа
Всякое комплексное число z= (x,y) можно изобразить как точку на плоскости с координатамиxиy. Плоскость, на которой изображаются комплексные числа, называетсякомплексной плоскостью, при этом осьOxназываетсядействительной, аOy-мнимой.
Расстояние rточкиzот нулевой точки, т. е. число
![]()
![]()
называется модулемкомплексного числаzи обозначается символом |z|.
Число
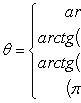
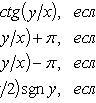

называем
аргументомкомплексного числаzи обозначаем символомθ= argz.
При заданномrуглы, отличающиеся
на![]()
![]() ,
соответствуют одному и тому же числу.
В этом случае записываем
,
соответствуют одному и тому же числу.
В этом случае записываем![]()
![]()
![]() называемглавным значениемаргумента.
называемглавным значениемаргумента.
Числа rиθназываютполярными координатамикомплексного числаz. В этом случае
z = (x, y) = (r cos θ, r sin θ) = r(cos θ + i sin θ)
называется тригонометрической формойкомплексного числа.
Если z1= (r1cosθ1,r1sinθ1),z2= (r2cosθ2,r2sinθ2), то
z1z2 = (r1r2 cos(θ1 + θ2), r1r2 sin(θ1 + θ2)),
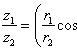
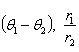
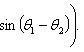
Для n-й степени числаz= (rcosθ,rsinθ) формула приобретает видzn= (rncosnθ,rnsinnθ).
При r= 1 соотношение приобретает видzn= (cosnθ, sinnθ) и называетсяформулой Муавра.
Корень n-й степени из комплексного числаzимеетnразличных значений, которые находятся по формуле
![]()
![]()
![]()
![]()
![]() (1)
(1)
Тригонометрическая форма комплексного числа
Пусть
![]() .
Положим
.
Положим![]() ,
,![]() .
Из рисунка 17.4 очевидно, что
.
Из рисунка 17.4 очевидно, что![]() Тогда
Тогда![]() .
Это выражение запишем в виде
.
Это выражение запишем в виде![]() (
17 .8) Последняя запись называется
тригонометрической формой комплексного
числа. В отличие от нее запись числа в
виде
(
17 .8) Последняя запись называется
тригонометрической формой комплексного
числа. В отличие от нее запись числа в
виде![]() называют
иногда алгебраической формой комплексного
числа. Отметим, что тригонометрическая
форма -- это указание числа по двум его
характеристикам: модулю и аргументу.
Поэтому вместо формулы ( 17.8 ) можно
было бы просто записывать пару
называют
иногда алгебраической формой комплексного
числа. Отметим, что тригонометрическая
форма -- это указание числа по двум его
характеристикам: модулю и аргументу.
Поэтому вместо формулы ( 17.8 ) можно
было бы просто записывать пару![]() ,
но запись ( 17.8 ) принята в силу традиции.
Замечание 17
. 3 При записи числа в тригонометрической
форме НЕЛЬЗЯ вычислять значения
,
но запись ( 17.8 ) принята в силу традиции.
Замечание 17
. 3 При записи числа в тригонометрической
форме НЕЛЬЗЯ вычислять значения![]() и
и![]() ,
иначе мы потеряем явное указание
аргумента
,
иначе мы потеряем явное указание
аргумента![]() и
снова вернемся к алгебраической форме.
Кроме того, если угол
и
снова вернемся к алгебраической форме.
Кроме того, если угол![]() получился
отрицательным, то знак "
получился
отрицательным, то знак "![]() "
НЕЛЬЗЯ выносить за знак синуса и НЕЛЬЗЯ
убирать его под знаком косинуса.
Пример 17 . 5
Запишите в тригонометрической форме
числа
"
НЕЛЬЗЯ выносить за знак синуса и НЕЛЬЗЯ
убирать его под знаком косинуса.
Пример 17 . 5
Запишите в тригонометрической форме
числа![]() ,
,![]() ,
,![]() ,
,![]() .
Решение. Находим модуль, аргумент, а
затем выписываем тригонометрическую
форму:
.
Решение. Находим модуль, аргумент, а
затем выписываем тригонометрическую
форму: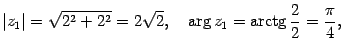
![]()
![]()
![]()
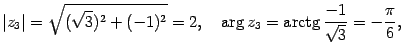
![]()
![]()
![]() Пусть
Пусть![]() ,
,![]() .
Найдем произведение
.
Найдем произведение![]() :
: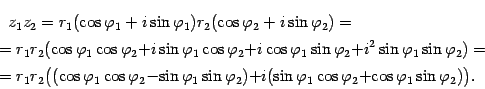 Заметим,
что во внутренних скобках стоят формулы
косинуса и синуса суммы аргументов.
Поэтому
Заметим,
что во внутренних скобках стоят формулы
косинуса и синуса суммы аргументов.
Поэтому![]() Последняя
запись является тригонометрической
формой комплексного числа
Последняя
запись является тригонометрической
формой комплексного числа![]() .
Значит,
.
Значит,![]()
![]() иными
словами, при умножении комплексных
чисел их модули перемножаются, а аргументы
складываются . Аналогично можно доказать,
что
иными
словами, при умножении комплексных
чисел их модули перемножаются, а аргументы
складываются . Аналогично можно доказать,
что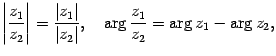 иными
словами, при делении комплексных чисел
их модули делятся один на другой, а
аргументы вычитаются . Несложно проверить,
что если
иными
словами, при делении комплексных чисел
их модули делятся один на другой, а
аргументы вычитаются . Несложно проверить,
что если![]() ,
то
,
то![]() Используя
правило умножения комплексных чисел в
тригонометрической форме, получим
формулу для возведения комплексного
числа в степень
Используя
правило умножения комплексных чисел в
тригонометрической форме, получим
формулу для возведения комплексного
числа в степень![]() ,
где
,
где![]() --
натуральное число. Пусть
--
натуральное число. Пусть![]() .
Тогда
.
Тогда![]() то
есть
то
есть![]() Далее
находим
Далее
находим![]() то
есть
то
есть![]() Продолжая
умножения дальше, придем к формуле
Продолжая
умножения дальше, придем к формуле![]() (
17 .9) Эта формула называется формулой
Муавра . Пример
17 . 6 Вычислите
(
17 .9) Эта формула называется формулой
Муавра . Пример
17 . 6 Вычислите![]() ,
если
,
если![]() .
Решение. Находим тригонометрическую
форму числа
.
Решение. Находим тригонометрическую
форму числа![]() :
:![]() По
формуле Муавра
По
формуле Муавра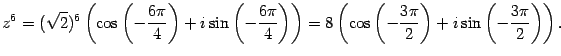 Переходим
к алгебраической форме, вычисляя косинус
и синус:
Переходим
к алгебраической форме, вычисляя косинус
и синус:![]() .
Ответ:
.
Ответ:![]() .
.
