
- •1.Матрица.Транспонированная матрица.Сложение и умножение на число.
- •2Отрицательная матрица
- •3Элементарные преобразования матрицы.Вырожденные и невырожденные.
- •4 Минора и алгеброические дополнения
- •6 Обратная матрица
- •7Ранг матрицы
- •Связанные определения
- •8Системы линейных уравнений
- •9Система линейных уравнений решение методом гаусса
- •10Решение системы с помощью обратной матрицы
- •11Кривые второго порядка
- •12Окружность
- •13Элиппс
- •14Гипербола
- •15Парабола
- •17Дифференци́рованием.
- •[Править] Определение производной функции через предел
- •18Правила дифференцирования
- •19Производная обратной функции
- •20Правило диференц. Сложн. Функ.
- •21И22 на листке.
- •23Производные от обратных тригонометрических функций
- •24Дифференциал
- •25Производные и дифференциалы высших порядков
- •26Дифференцирование функций, заданных параметрически
- •27Теорема Ферма
- •28И29Теоремы Ролля, Лагранжа, Коши
- •30Тейлора формула
- •31Раскрытие неопределенностей. Правило Лопиталя
- •32Точки экстремума
- •Необходимое условие экстремума
- •Достаточное условие экстремума
- •Общий план исследования функции и построения графика.
- •35Неопределенный интеграл и его свойства. Таблица интегралов.
- •36Метод замены переменной (метод подстановки)
- •Интегрирование по частям
- •37Интегрирование рациональных выражений
- •38Эйлера подстановки
- •39Определения
- •41Определения
- •Стандартная модель
- •Матричная модель
- •Замечания
- •Модуль и аргумент
- •Сопряжённые числа
- •Алгебраическая форма
- •Тригонометрическая и показательная формы
- •42Геометрическая интерпретация комплексного числа
6 Обратная матрица
Матрица
![]() называется
обратной матрицей для квадратной матрицы
называется
обратной матрицей для квадратной матрицы
![]() ,
если
,
если
![]() .
Из определения
следует, что обратная матрица
.
Из определения
следует, что обратная матрица
![]() будет
квадратной матрицей того же порядка,
что и матрица
будет
квадратной матрицей того же порядка,
что и матрица
![]() (иначе
одно из произведений
(иначе
одно из произведений
![]() или
или
![]() было
бы не определено). Обратная матрица для
матрицы
было
бы не определено). Обратная матрица для
матрицы
![]() обозначается
обозначается
![]() .
Таким образом, если
.
Таким образом, если
![]() существует,
то
существует,
то
![]() .
Из определения обратной матрицы следует,
что матрица
.
Из определения обратной матрицы следует,
что матрица
![]() является
обратной для матрицы
является
обратной для матрицы
![]() ,
то есть
,
то есть
![]() .
Про матрицы
.
Про матрицы
![]() и
и
![]() можно
говорить, что они обратны друг другу
или взаимно обратны. Предложение
14 . 20 Если матрица
можно
говорить, что они обратны друг другу
или взаимно обратны. Предложение
14 . 20 Если матрица
![]() имеет
обратную, то
имеет
обратную, то
![]() и
и
![]() .
Доказательство
. Так как определитель
произведения матриц равен произведению
определителей ( предложение 14.7 ), то
.
Доказательство
. Так как определитель
произведения матриц равен произведению
определителей ( предложение 14.7 ), то
![]() .
По следствию 14.1
.
По следствию 14.1
![]() ,
поэтому
,
поэтому
![]() ,
что невозможно при
,
что невозможно при
![]() .
Из предыдущего равенства следует также
.
Из предыдущего равенства следует также
![]() .
Последнее предложение
можно сформулировать в следующем виде.
Если определитель матрицы равен нулю,
то обратная к ней не существует. Так как
для нахождения обратной матрицы важно,
равен ли определитель марицы нулю или
нет, то введем следующие определения.
Определение
14 . 9 Квадратную матрицу
.
Последнее предложение
можно сформулировать в следующем виде.
Если определитель матрицы равен нулю,
то обратная к ней не существует. Так как
для нахождения обратной матрицы важно,
равен ли определитель марицы нулю или
нет, то введем следующие определения.
Определение
14 . 9 Квадратную матрицу
![]() назовем
вырожденной или особенной матрицей ,
если
назовем
вырожденной или особенной матрицей ,
если
![]() ,
и невырожденной или неособенной матрицей
, если
,
и невырожденной или неособенной матрицей
, если
![]() .
Предложение
14 . 21 Если обратная матрица существует,
то она единственна.
Доказательство . Пусть две
матрицы
.
Предложение
14 . 21 Если обратная матрица существует,
то она единственна.
Доказательство . Пусть две
матрицы
![]() и
и
![]() являются
обратными для матрицы
являются
обратными для матрицы
![]() .
Тогда
.
Тогда
![]() и
и![]() Следовательно,
Следовательно,
![]() .
Предложение
14 . 22 Если квадратная матрица
.
Предложение
14 . 22 Если квадратная матрица
![]() является
невырожденной, то обратная для нее
существует и
является
невырожденной, то обратная для нее
существует и
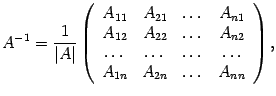 (
14 .14) где
(
14 .14) где
![]() --
алгебраические дополнения к элементам
--
алгебраические дополнения к элементам
![]() .
Доказательство
. Так как для невырожденной
матрицы
.
Доказательство
. Так как для невырожденной
матрицы
![]() правая
часть равенства ( 14.14 ) всегда существует,
то достаточно показать, что эта правая
часть является обратной матрицей для
матрицы
правая
часть равенства ( 14.14 ) всегда существует,
то достаточно показать, что эта правая
часть является обратной матрицей для
матрицы
![]() .
Обозначим правую часть равенства (
14.14 ) буквой
.
Обозначим правую часть равенства (
14.14 ) буквой
![]() .
Тогда нужно проверить, что
.
Тогда нужно проверить, что
![]() и
что
и
что
![]() .
Докажем первое из этих равенств, второе
доказывается аналогично. Пусть
.
Докажем первое из этих равенств, второе
доказывается аналогично. Пусть
![]() .
Найдем элементы матрицы
.
Найдем элементы матрицы
![]() ,
учитывая, что
,
учитывая, что
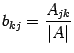 :
:
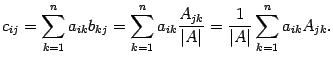 Если
Если
![]() ,
то по предложению 14.17 сумма справа
равна нулю, то есть
,
то по предложению 14.17 сумма справа
равна нулю, то есть
![]() при
при
![]() .
Если
.
Если
![]() ,
то
,
то
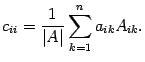 Сумма
справа представляет собой разложение
определителя матрицы
Сумма
справа представляет собой разложение
определителя матрицы
![]() по
по
![]() -ой
строке ( предложение 14.16 ). Таким образом,
-ой
строке ( предложение 14.16 ). Таким образом,
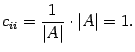 Итак,
в матрице
Итак,
в матрице
![]() диагональные
элементы равны 1, а остальные равны нулю,
то есть
диагональные
элементы равны 1, а остальные равны нулю,
то есть
![]() .
Результаты предложений
14.20 , 14.21 , 14.22 соберем в одну теорему.
Теорема 14 . 1
Обратная матрица для квадратной
матрицы
.
Результаты предложений
14.20 , 14.21 , 14.22 соберем в одну теорему.
Теорема 14 . 1
Обратная матрица для квадратной
матрицы
![]() существует
тогда и только тогда, когда матрица
существует
тогда и только тогда, когда матрица
![]() --
невырожденная, обратная матрица
единственна, и справедлива формула (
14.14 ). Замечание
14 . 12 Следует обратить особое внимание
на места, занимаемые алгебраическими
дополнениями в формуле обратной матрицы:
первый индекс показывает номер столбца
, а второй -- номер строки , в которые
нужно записать вычисленное алгебраическое
дополнение.
Пример 14 . 7
Найдите обратную матрицу для матрицы
--
невырожденная, обратная матрица
единственна, и справедлива формула (
14.14 ). Замечание
14 . 12 Следует обратить особое внимание
на места, занимаемые алгебраическими
дополнениями в формуле обратной матрицы:
первый индекс показывает номер столбца
, а второй -- номер строки , в которые
нужно записать вычисленное алгебраическое
дополнение.
Пример 14 . 7
Найдите обратную матрицу для матрицы
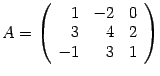 .
Решение. Находим определитель
.
Решение. Находим определитель
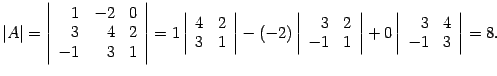 Так
как
Так
как
![]() ,
то матрица
,
то матрица
![]() --
невырожденная, и обратная для нее
существует. Находим алгебраические
дополнения:
--
невырожденная, и обратная для нее
существует. Находим алгебраические
дополнения:
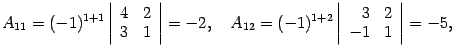
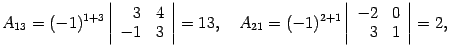

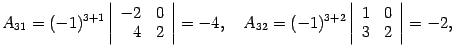
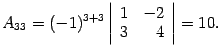 Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй -- строке:
Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй -- строке:
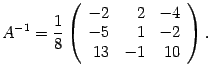 (
14 .15) Полученная матрица и служит ответом
к задаче.
Замечание 14
. 13 В предыдущем примере было бы
точнее ответ записать так:
(
14 .15) Полученная матрица и служит ответом
к задаче.
Замечание 14
. 13 В предыдущем примере было бы
точнее ответ записать так:
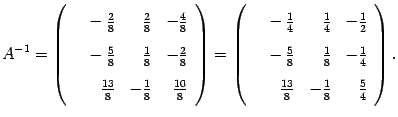 (
14 .16) Однако запись ( 14.15 ) более компактна
и с ней удобнее проводить дальнейшие
вычисления, если таковые потребуются.
Поэтому запись ответа в виде ( 14.15 )
предпочтительнее, если элементы матриц --
целые числа. И наоборот, если элементы
матрицы
(
14 .16) Однако запись ( 14.15 ) более компактна
и с ней удобнее проводить дальнейшие
вычисления, если таковые потребуются.
Поэтому запись ответа в виде ( 14.15 )
предпочтительнее, если элементы матриц --
целые числа. И наоборот, если элементы
матрицы
![]() --
десятичные дроби, то обратную матрицу
лучше записать без множителя
--
десятичные дроби, то обратную матрицу
лучше записать без множителя
![]() впереди.
Замечание
14 . 14 При нахождении обратной матрицы
приходится выполнять довольно много
вычислений и необычно правило расстановки
алгебраических дополнений в итоговой
матрице. Поэтому велика вероятность
ошибки. Чтобы избежать ошибок следует
делать проверку: вычислить произведение
исходной матрицы на итоговую в том или
ином порядке. Если в результате получится
единичная матрица, то обратная матрица
найдена правильно. В противном случае
нужно искать ошибку.
Пример 14 . 8
Найдите обратную матрицу для матрицы
впереди.
Замечание
14 . 14 При нахождении обратной матрицы
приходится выполнять довольно много
вычислений и необычно правило расстановки
алгебраических дополнений в итоговой
матрице. Поэтому велика вероятность
ошибки. Чтобы избежать ошибок следует
делать проверку: вычислить произведение
исходной матрицы на итоговую в том или
ином порядке. Если в результате получится
единичная матрица, то обратная матрица
найдена правильно. В противном случае
нужно искать ошибку.
Пример 14 . 8
Найдите обратную матрицу для матрицы
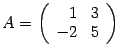 .
Решение.
.
Решение.
![]() --
существует.
--
существует.
![]()
![]() Ответ:
Ответ:
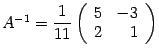 .
Нахождение
обратной матрицы по формуле ( 14.14 )
требует слишком много вычислений. Для
матриц четвертого порядка и выше это
неприемлемо. Реальный алгоритм нахождения
обратной матрицы будет приведен позже.
.
Нахождение
обратной матрицы по формуле ( 14.14 )
требует слишком много вычислений. Для
матриц четвертого порядка и выше это
неприемлемо. Реальный алгоритм нахождения
обратной матрицы будет приведен позже.
