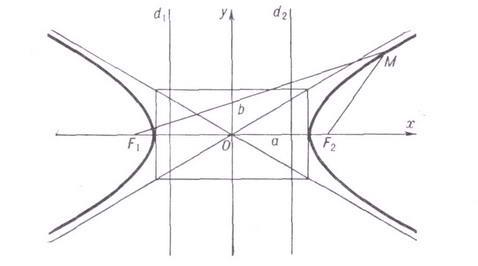
14Гипербола

- плоская кривая, получающаяся в пересечении кругового конуса с плоскостью, не проходящей через вершину конуса и пересекающей обе его полости. Г. есть множество точек Мплоскости (см. рис.), модуль разности расстояний к-рых до двух данных точек и (фокусов Г.) постоянен и равен . Расстояние между фокусами Г. наз. ф о-кусным расстоянием его принято обозначать через2с.Середина отрезка наз. центром Г. Прямая, на к-рой лежат фокусы Г., наз. действительной (или фокальной) осью Г. Прямая, проходящая через центр Г. перпендикулярно к действительной оси Г., наз. мнимой осью Г. Мнимая и действительная оси Г. являются ее осями симметрии. Число наз. эксцентриситетом Г. Диаметром Г. наз. любая прямая, проходящая через центр Г. Середины параллельных хорд Г. лежат на диаметре. Директрисой Г., соответствующей данному фокусуF,наз. прямаяd,перпендикулярная к действительной оси Г., отстоящая от центра на расстояниеaleи лежащая от центра по одну сторону с фокусомF.У Г.- две директрисы. Г. имеет две асимптоты:

Г. есть центральная линия второго порядка.Ее канонич. уравнение имеет вид

где и - полуоси Г., а - текущие координаты. Уравнение касательной к Г. в точке (x₀, y₀) имеет вид

Фокальный параметр Г. (половина длины хорды, проходящей через фокус перпендикулярно фокальной оси Г.) равен . При помощи фокального параметра рможно записать уравнение Г. в виде

где - полярные координаты, - угол между асимптотами.

При Г. наз. равнобочной, или равносторонней, Г. Асимптоты равнобочной Г. взаимно перпендикулярны; если их принять за оси координат, то уравнение равнобочной Г. примет вид

т. е. равнобочная Г. представляет собой график обратно пропорциональной зависимости.

15Парабола

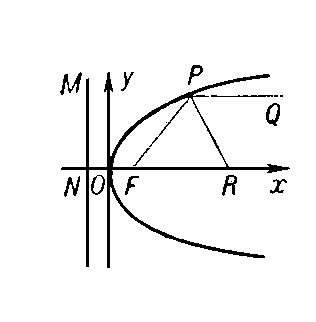
линия пересечения круглого конуса плоскостью, параллельной какой-либо касательной плоскости этого конуса (рис. 1). П. может быть также определена как геометрическое место точек плоскости (рис. 2), для каждой из которых расстояние до определённой точки F плоскости — фокуса П.— равно расстоянию до некоторой прямой MN — директрисы П. Прямая, проходящая через фокус перпендикулярно директрисе и направленная от директрисы к фокусу, называется осью П., а точка пересечения оси с П.— вершиной П. Если выбрать систему координат хОу так, как указано на рис. 2, то уравнение П. примет вид:

         у² = 2рх,

        где р — длина отрезка FN. Величина р называется параметром П. Парабола — линия второго порядка (См. Линии второго порядка). График квадратного трёхчлена у = ax² + bx + c является П. Парабола представляет собой бесконечно простирающуюся кривую, симметричную относительно оси. Если в фокусе П. поместить источник света, то лучи, отразившиеся от П., образуют параллельный пучок, т.к. прямая PF, соединяющая любую точку Р П. с фокусом, и прямая, параллельная оси, образует с нормалью PR равные углы. Это свойство П. применяется, например, для прожекторных устройств (см. Параболическая антенна). См. также Конические сечения.

        

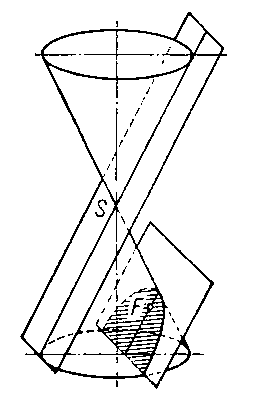
        Рис. 1 к ст. Парабола.

        

16понятия производной функции.

Физический смысл производной x`(t) от непрерывной функции x(t) в точке t₀ – есть мгновенная скорость изменения величины функции, при условии, что изменение аргумента Δt стремится к нулю. Таким образом, мгновенная скорость (величина пути, пройденного за мгновение) и есть производная величина от функции, описывающей путь самолёта по времени. Мгновенная скорость - это и есть физический смысл производной.

Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение  x 0, причем x+ x  (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+ x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+ x,f(x+ x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОX через  ( x).

Определение 3. Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при  x 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика.

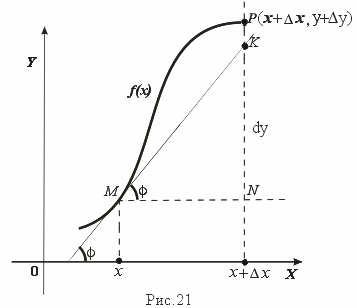
Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел lim_{ x 0} ( x) =  ₀, который равен углу, образованному касательной с положительным направлением оси OX.

Справедливо утверждение:

Предложение 1. Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке M( x,f(x)) , причем угловой коэффициент этой касательной равен производной f'(x).

Из этого утверждения вытекает геометрический смысл производной: производная f'(x0) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x0, который в свою очередь равен tg угла наклона касательной к графику функции.

Тогда уравнение касательной к кривой f(x) в точке x₀ имеет вид

y = f(x0)+f'(x0)(x-x0)

Пример 3. Составить уравнение касательной к кривой y = 2x²-x+5 при x = -0,5.

Решение. Найдем производную в точке x = -0,5

y' = 4x-1, y'(-0,5) = -3.

Уравнение касательной имеет вид:

y = 6-3(x+0,5) или y = -3x+4,5.

h4>Дифференцируемость функции Пусть функция определена на интервале (a,b).