1. Цепь из последовательно соединенных звеньев

(рис. 2.1). Пусть заданы передаточные функции всех звеньев:

где X_i=X_i(s)—изображения по Лапласу переменных x_i(t). Передаточная функция всей цепи, по определению, будет

Если перемножить между собой все левые части и все правые части написанных равенств, получим иско­мый результат

так как все промежуточные переменные X_i при таком перемножении сокращаются. Следовательно,

т. е. передаточная функция разомкнутой цепи последо­вательно соединенных звеньев равна произведению пе­редаточных функций всех звеньев.

2. Цепь из параллельно соединенных звеньев (рис. 2.2). Пусть заданы передаточные функции звеньев

Поскольку выходная величина цепи равна

то и передаточная функция цепи получит вид

т. е. передаточная функция разомкнутой цепи из парал­лельно соединенных звеньев равна сумме передаточных функций всех звеньев.

3. Цепь с местной обратной связью (рис. 2.3). Запи­шем сначала передаточную функцию звена, охваченного

обратной связью (часть схемы, обведенная на рис. 2.3 пунктиром).

Обратная связь называется отрицательной, если (см. рис. 2.3)

Согласно схеме имеем в изображениях по Лапласу

Отсюда получаем

Перемножив правую часть данного выражения с переда­точными функциями остальных звеньев цепи (согласно формуле (2.1)), получаем окончательную формулу

т. е. передаточная функция разомкнутой цепи с местной отрицательной обратной связью равна произведению пе­редаточных функций всех звеньев прямой цепи, деленно­му на единицу плюс произведение передаточной функ­ции обратной связи на передаточную функцию охваты­ваемого ею звена.

Если в той же схеме (рис. 2.3) местная обратная связь будет положительной, т. е. если х₂=х₁ + x_oc , то получим

Отличие заключается в знаке второго слагаемого зна­менателя. Это, как увидим потом, весьма важно. Главное применение в автоматических системах имеют отрица­тельные обратные связи.

В общем случае, сложная разомкнутая цепь звеньев может включать в себя комбинации всех трех рассмот­ренных случаев. Пользуясь полученными здесь форму­лами, можно составлять общую передаточную функцию и для более сложных цепей (см. об этом ниже § 2.2).

Общий коэффициент усиления разомкнутой цепи. Це­лесообразно, как и для отдельного звена, передаточную функцию всей разомкнутой цепи в целом W(s) приво­дить к стандартному виду

где N(s) и L(s) — многочлены с единичными коэффи­циентами при младших членах. Выносимый при этом множитель К явится общим коэффициентом усиления всей разомкнутой цепи звеньев. Согласно записанным выше формулам получим:

а) для цепи из последовательно соединенных звеньев (рис. 2.1)

где k_i—коэффициенты усиления отдельных звеньев;

б) для цепи из параллельно соединенных позицион­ных звеньев (рис. 2.2)

в) для цепи с отрицательной местной обратной связью (рис. 2.3) в случае, если звенья W₂ и W_oc —по­зиционные,

а при положительной местной обратной связи

В случае наличия непозиционных звеньев формулы (2.5) и (2.6) изменятся (см. гл. 6).

Заметим, что степень числителя KN(s) передаточной функции разомкнутой цепи звеньев в реальных системах обычно ниже степени знаменателя L(s).

Дифференциальное уравнение разомкнутой цепи будет

а характеристическое уравнение —

Частотные характеристики разомкнутой цепи звеньев.

Рассмотрим получение частотных характеристик на при­мере, из которого будет ясен общий метод. Пусть задана передаточная функция разомкнутой цепи в виде

причем ζ = 0,6 (при таком ζ можно будет не учитывать «горба» амплитудной частотной характеристики колеба­тельного звена).

Амплитудная и фазовая частотные характеристики имеют вид

Их можно изобразить графически (рис. 2.4), а по ним — построить и амплитудно-фазовую частотную ха­рактеристику (рис. 2.5).

Логарифмическую амплитудно-частотную характери­стику можно строить непосредственно по заданной пе­редаточной функции. Для этого надо помнить, что, со­гласно характеристикам типовых звеньев (см. главу 1),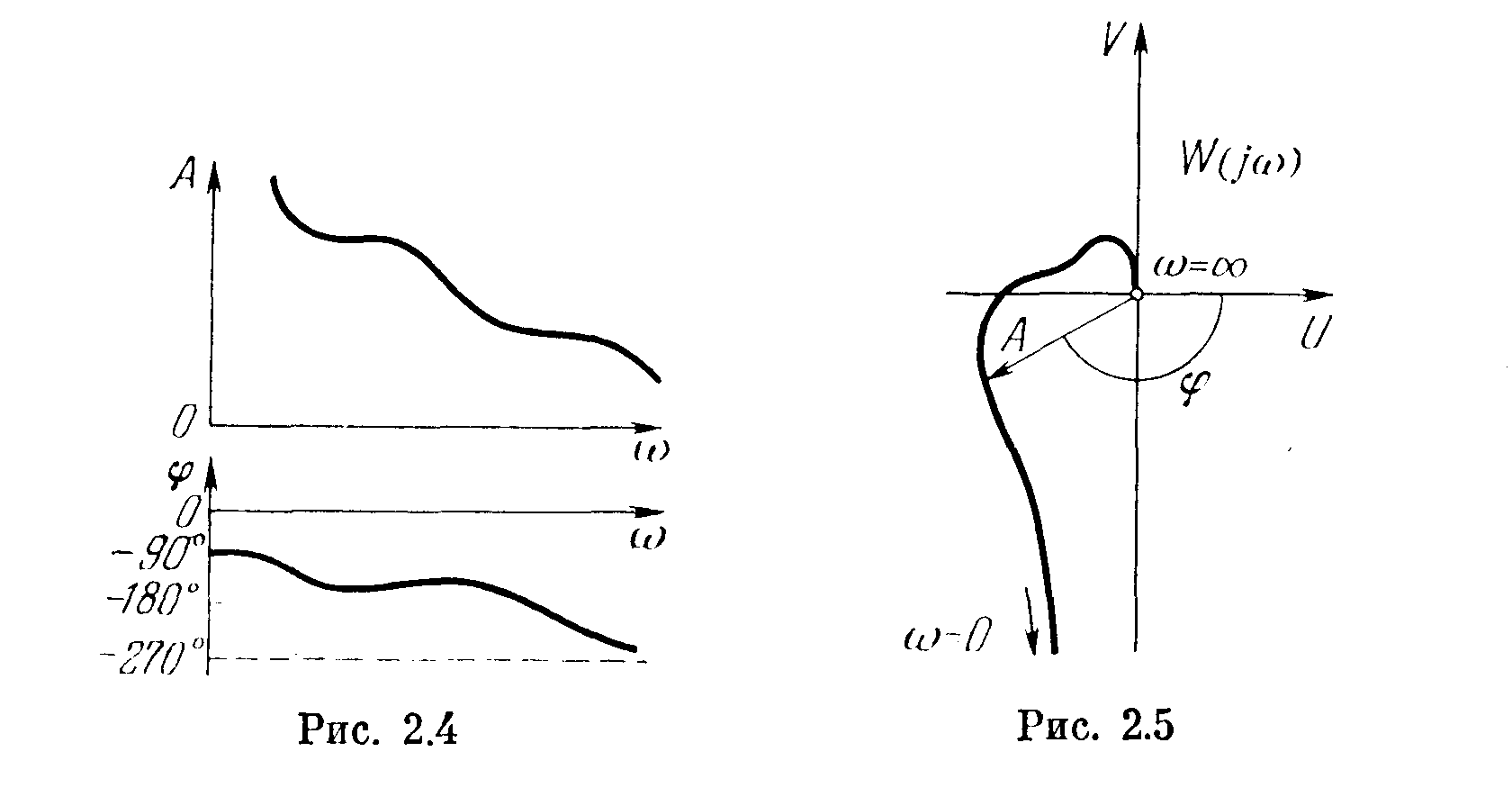

каждому сомножителю типа (Ts+l) в знаменателе со­ответствует точка излома характеристики при с последующим наклоном —20дБ/дек., а каждому сомножи­телю такого же типа в числителе соответствует точка излома при с последующим наклоном +20 дБ/дек.

Сомножителю же типа (T²s²+2ζT_s+1) в знаменателе соответствует излом при с наклоном —40 дБ/дек, если 0,5 < ζ < 1. При ζ < 0,5 нужно добавочно строить «горб», вычислив превышение Н (см. § 1.2).

Таким образом, пронумеровав по порядку все сомно­жители передаточной функции:

для каждого из них получим характеристики, показанные па рис. 2.6, а и обозначенные там цифрами в круж­-

ках. Простое сложение их дает искомую логарифмиче­скую амплитудную частотную характеристику Lm(ω) данной разомкнутой цепи звеньев, показанную на рис. 2.6, б. На рис. 2.6, в согласно написанной выше формуле изображена фазовая частотная характеристи­ка φ(ω).

Из рис. 2.6 видно, что легко можно строить непосред­ственно суммарную характеристику Lm(ω) по переда­точной функции W(s) (помня указанное выше правило изломов), не изображая отдельных частей характеристи­ки (т. е. можно обойтись без рис. 2.6, а). При этом частоты в точках изломов называются сопрягающими частотами.

При более сложных формах передаточной функции W(s), например, при наличии внутренних обратных связей, построение ЛАХ усложняется. Однако часто мож­но и сложные формулы приводить к аналогичному виду, разложив на множители многочлены числителя и зна­менателя (с заданными числовыми коэффициентами). Имеются и другие инженерные приемы.

Для любой разомкнутой цепи звеньев, как ранее де­лалось для отдельного звена, можно определить также переходные и весовые функции.