
Mech-Slobod
.pdfДодаток 3
Параметричний резонанс
Можливість параметричного збудження коливань і параметричного резонансу можна показати й виходячи з рівняння руху найпростішої коливальній системі без згасання і без зовнішньої періодичної змушуючої сили
x +ω 2 (t)x =0 , |
(Д3.1) |
0 |
|
де залежність параметра ω02 (t) від часу має місце внаслідок явної залежності від часу одного |
|
або декількох параметрів, що визначають період власних |
коливань осцилятора: довжини |
математичного маятника l, коефіцієнта пружності пружини k , |
моменту інерції I для фізичного |
маятника тощо. |
|
Покажемо, що при періодичній зміні параметра ω0 можливе експоненціальне зростання зміщення x .
Розглянемо умови виникнення параметричного резонансу у простому випадку, коли функція
ω02 (t) мало відрізняється від постійної величини ω02 , яка є квадратом частоти власних коливань
системи для певного рівноважного (початкового) значення параметра, що змінюється з часом, і є простою періодичною функцією
ω02 (t) = ω02 (1 + ε cosΩt) , |
(Д3.2) |
де стала ε є додатно визначена і набагато менша за одиницю, |
1 >> ε > 0 . Враховуючи |
результат спостережень за параметричним розгойдуванням гойдалки (зміна параметра l двічі за
період власних коливань T =2π/ω ), покладемо |
Ω = 2ω + δω , |
де |
δω << ω |
. Тоді рівняння руху |
|
|
0 |
0 |
|
0 |
|
параметрично збуджуваного осцилятора набирає вигляду |
|
|
|
||
x + ω02[1 + ε cos(2ω0 + δω)t]x = 0 . |
|
|
|
(Д3.3) |
|
Розв’язок цього рівняння шукаємо у вигляді |
|
|
|
||
x(t) = a(t)cos(ω0 + δω / 2)t + b(t)sin(ω0 + δω / 2)t , |
|
|
(Д3.4) |
||
де a(t) і |
b(t) є функції, що повільно |
змінюються з |
часом порівняно з множниками |
||
cos(ω0 + δω / 2)t |
і sin(ω0 + δω / 2)t . Такий вигляд розв’язку є наближеним і враховує лише члени |
||||
першого порядку малості по ε . Підставимо (Д3.4) в (Д3.3) і перетворимо добутки тригонометричних функцій на суми, наприклад,
cos(ω |
0 |
+ δω / 2)t cos(2ω + δω)t = |
1 |
cos(3ω |
0 |
+ 3δω / 2)t + |
1 |
cos(ω |
0 |
+ δω / 2)t |
(Д3.5) |
|
|
|
|||||||||||
|
|
0 |
2 |
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
При цьому збережемо лише члени першого порядку по малому параметру δω , при |
||||||||||||
додатковому припущенні, |
що a(t) δωa(t) і |
b(t) δωa(t) , |
правильність якого підтверджується |
|||||||||
результатом, отриманим для резонансу, а також, випустимо доданки з частотами 3(ω0 +δω / 2) , як
такі, що є вищого порядку по ε . У результаті таких спрощень отримаємо
− (2a + bδω + bεω0 / 2)ω0 sin[(ω0 + δω / 2)t] + (2b − aδω + εω0a / 2)ω0 cos[(ω0 + δω / 2)t] = 0 . (Д3.6)
Ця рівність виконується для будь-якого моменту часу тоді і лише тоді, коли коефіцієнти при синусі та косинусі одночасно дорівнюють нулю:
2a + bδω + εω0b / 2 = 0 |
|
2b |
(Д3.6) |
− aδω + εω0a / 2 = 0 |
|
Розв’язок цієї системи двох лінійних диференційних рівнянь за загальними правилами
шукаємо у вигляді a = a0eαt та b = b0eαt і після його підстановки до (Д3.6) одержимо систему для
знаходження α :
αa + (δω + εω0 / 2)b / 2 = 0 |
|
|
|
|
|
|
|
|
(Д3.7) |
||||||||||
(δω − εω0 / 2)a / 2 − αb = 0 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Умовою сумісності системи двох алгебраїчних рівнянь (Д3.7) є рівність її визначника нулю: |
|||||||||||||||||||
|
|
|
|
α |
|
δω + εω0 / 2 |
|
2 |
|
1 |
|
2 |
εω0 |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
δω − εω0 / 2 |
− α |
|
|
|
= −α |
|
− |
|
[(δω) |
|
− |
] = 0 , |
(Д3.8) |
|||||
|
|
|
|
|
4 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
звідки знаходимо |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
1 |
εω0 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
α |
|
= |
|
|
|
− (δω) |
|
. |
|
|
|
|
|
|
|
|
(Д3.9) |
||
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оскільки розв’язок (Д3.4) має бути дійсним, дійсними мають бути і амплітуди a(t) |
і b(t) при |
||||||||||||||||||
синусі та косинусі. Отже, |
параметр α теж повинен бути дійсним, тобто α 2 > 0 . Це можливо тоді, |
||||||||||||||||||
коли |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
εω0 |
< δω < |
εω0 , |
|
|
|
|
|
|
|
|
|
|
|
(Д3.10) |
||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
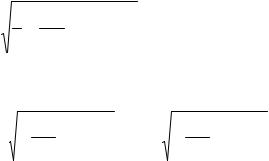
тобто параметричний резонанс може мати місце у деякому інтервалі поблизу частоти 2ω0 , ширина
якого пропорційна величині ε , що визначає глибину параметричної модуляції. Параметричний
резонанс має місце і на частотах зміни параметра коливної системи Ω близьких до 2ω0 / n , де n –
будь-яке ціле число. Це відповідає досвіду: при розгойдуванні гойдалки можна присідати й один раз за період або за декілька періодів. Але ширина резонансних ділянок частот при збільшенні n
швидко зменшується як підсилення α .
Вищенаведений розгляд умов виникнення нестійкості коливної системи при періодичній зміні її параметра, що визначає власну частоту коливань було здійснено для недисипативної системи. З досвіду ж відомо, що параметричний резонанс спостерігається і при наявності дисипативних сил. Як було показано в 8.1.2, амплітуда коливань, що згасають внаслідок наявності
сили опору пропорційної швидкості, змінюється за законом e− βt . Тому збільшення амплітуди
коливань в умовах параметричного резонансу при наявності тертя відбувається за законом e(α − β )t ,
причому для зростання амплітуди коливань з часом необхідно, щоб показник степеня в експоненті
був додатним α − β > 0 , тобто показник підсилення був би більшим за показник згасання.
Границя області нестійкості визначається рівністю α − β = 0 , яку, з врахуванням (Д3.9) можна переписати у вигляді
|
1 |
εω0 |
|
2 |
|
|
|
2 |
|
− α = 0 , |
|
|
|
|
(Д3.11) |
|||
|
4 |
|
2 |
|
|
− (δω ) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
звідки отримуємо |
|
|
|
|
|
|
|
|
|
|
|
|||||||
− |
εω0 |
|
2 |
− 4α |
2 |
|
< |
δω < |
εω0 |
2 |
− 4α |
2 |
|
(Д3.12) |
||||
|
2 |
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Як видно з (Д3.12) при наявності сил опору параметричний резонанс можливий не при як завгодно малій амплітуді ε , а лише починаючи з її деякого мінімального (порогового) значення
ε ïîð , яке для збудження поблизу частоти 2ω0 |
становить |
|||
ε ïîð |
= |
4α |
. |
(Д3.13) |
|
||||
|
|
ω0 |
|
|
