
Sysoev_TeorosnovyTMSlekc
.pdf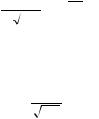
F = |
|
1 |
X A − x2 |
|
σ |
∫ |
e 2a 2 . |
||
a |
2π |
|
||
|
|
|
|
|
|
|
|
0 |
|
Для табулирования получено уравнение:
|
= Ф( z) = |
1 |
Z A |
− z 2 |
Fa |
2π |
∫ e 2 . |
||
|
|
0 |
|
|
По этому уравнению в приложении 1 составлены таблицы Ф(z) при различных значениях безразмерного квантиля распределения (коэффициента) z (dx=σdz). Вся площадь под кривой нормального распределения F=1.
Для практических целей нет необходимости использовать бесконечные пределы: в интервале x= ±0,7σ (z= ±0,7) 50%F, x= ±3σ (99,73%F). Поэтому считают, что все поле рассеивания параметра лежит в интервале ± 3σ при ошибке 0,27% . Тогда все поле рассеивания равно: ωp = 6σ.
6.2. Расчетно - аналитический метод определения
суммарных погрешностей
Последовательность определения суммарной погрешности:
изучение условий изготовления (способ обработки, характеристика станка, режущего и измерительного инструментов, режимов резания, испытаний и т. д.);
выявление перечня факторов, обуславливающих появление первичных погрешностей изготовления;
определение значений первичных погрешностей, вызываемых действием каждого из факторов, внесенных в перечень, используя формулы расчета элементарных погрешностей. В большинстве случаев задача заключается в определении поля погрешностей. Когда величину погрешности установить нельзя, используют нормативные и справочные данные (например, погрешность установки деталей в патроне, в тисках и т. п.);
установление законов распределения для каждой из первичных погрешностей установки, обработки и испытания. Их нельзя просто сложить, так как они найдены для худших условий, но их сочетание в таком виде маловероятно. Поэтому следует учитывать, что:
а) случайные погрешности, подчиняющиеся закону нормального распределения, складываются по правилу квадратичного корня;
б) случайные погрешности, подчиняющиеся другим законам, и закономерно - изменяющиеся погрешности суммируются с учетом закона их распределения;
в) систематические постоянные погрешности складываются алгебраически с учетом их знака, а для генеральной совокупности - арифметически.

Для генеральной совокупности погрешности изготовления определяют по формуле:
|
ωГС = ∑ωicп + k1 ∑ki2ωсл2 + ∑ki2ωi2з , (6.1) |
||
|
|
Σ |
|
где ωiсn - систематические постоянные погрешности; |
|||
ωiсл – |
случайные погрешности; |
|
|
ωiз – |
закономерно - изменяющиеся погрешности; |
||
ki и kΣ - коэффициенты относительного рассеивания соответствующих |
|||
погрешностей и их сумма: закон Гаусса - kiг =1; |
закон Симпсона - kiс = 1,22; |
||
закон равной вероятности - kip =1,73. |
|
||
В пределах отдельно взятой партии: |
|
||
|
ωГС = k1 |
∑ki2ωсл2 + ∑ki2ωi2з . |
(6.2) |
|
∑ |
|
|
Используя формулы 6.1 и 6.2 можно рассчитывать погрешность любого параметра в изготовленной партии изделия либо генеральной совокупности, представляющей технологический процесс по стабильному технологическому процессу.
6.3.Статистический метод определения суммарной погрешности
Воснову метода положены законы теории вероятности и математической статистики [10], например, частота появления события в прошлом при увеличении числа событий приближается к вероятности появления его в будущем. Использование статистического метода позволяет прогнозировать точность изготовления изделий.
При статистическом анализе точности необходимо соблюдение следующих требований:
для анализа следует брать параметры изделий, изготовленных при стабильных условиях;
число деталей в выборке должно быть значительным; измерение параметров должно выполняться инструментом или прибора-
ми, цена деления которых должна быть: 1/6...1/10δ , где δ - допуск на параметр.
Рассмотрим применение статистического метода на следующем приме-
ре.
Условие:
давление за насосом «О» должно быть Р = 20-0,2 МПа. При испытании ТНА получены давления жидкости и занесены в табл. 6.1. Построить практическую и теоретическую кривые распределения.
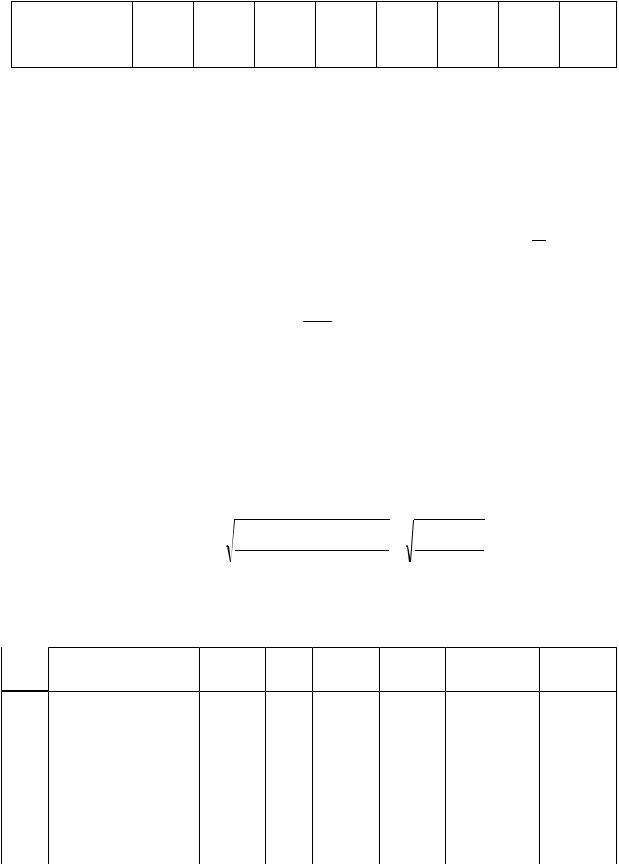
Таблица 6.1
Результаты измерения давления по линии «О» при проливе, Р, МПа
19,93 |
19,97 |
19,96 |
19,97 |
19,92 |
19,91 |
19,90 |
19,90 |
19,90 |
19,91 |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
19,95 |
19,94 |
19,88 |
19,95 |
19,97 |
19,90 |
19,91 |
19,91 |
19,92 |
19,90 |
Решение задачи выполняют в следующей последовательности. 1. Вычисляют практическое поле рассеивания:
wф = Xmax - Xmin ;
wф = X97 - X14 = 0,13 МПа.
2. Распределяют величину R на разряды К при условии: N = 50... 100 из-
делий, К = 5...7; а если N ³ 100, то K = 7...11. Цена разрядов C = R |
должна |
K |
|
быть больше цены деления измерительного инструмента для того, чтобы уменьшить влияние погрешности измерения:
при К = 7, C = 0,13 = 0,0185, С = 0,02 МПа. 7
3. Вычисляют статистический центр группирования по формуле:
_ |
∑xi ni |
, |
x = |
N |
|
|
|
где xi - значения представителей разрядов;
ni - частота в разряде (количество деталей).
4. Вычисляют среднеквадратическое отклонение по формуле
|
_ 2 |
n1 |
|
_ |
2 |
|
_ |
|
2 |
|
x1 |
− x |
+ ... xk |
− x |
nk |
xi |
− x |
|
ni |
. |
|
σ = |
|
|
|
|
|
= |
N |
|
|
|
|
|
|
N |
|
|
|
|
|
|
5. Для выполнения расчетов заполняют табл. 6.2.
Таблица 6.2
Расчетные данные для построения полигона распределения
№ К |
Границы |
хi |
ni |
хini |
хi - хср |
(хi - хср)2 |
(хi - |
|
разрядов |
|
|
|
|
|
хср)2ni |
1 |
19,855 до18,975 |
19,87 |
3 |
59,61 |
-0,06 |
0,0036 |
0,0108 |
2 |
19,875 до 19,895 |
19,89 |
16 |
318,24 |
-0,04 |
0,0016 |
0,0256 |
3 |
19,895 до 19,915 |
19,91 |
22 |
438,02 |
-0,02 |
0,0004 |
0,0088 |
4 |
19,915 до 19,935 |
19,93 |
25 |
438,25 |
0,01 |
0,0019 |
0,0059 |
5 |
19,935 до 19,955 |
19,95 |
19 |
379,05 |
0,02 |
0,0004 |
0,0076 |
6 |
19,955 до 19,975 |
19,97 |
13 |
259,61 |
0,04 |
0,0016 |
0,0208 |
7 |
19,975 до 19,995 |
19,99 |
2 |
39,98 |
0,06 |
0,0036 |
0,0072 |

|
|
х = |
∑ хi |
|
|
Σ |
|
∑ (xi − x )2 = |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
N |
|
|
100 |
0,0808 |
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
Среднее значение параметра |
х = 19,93; σ = 0,028. |
|
|
|
|||||
Рис. 6.1. Кривые распределения: 1 – практическая, 2 – теоретическая
6. Строят практическую кривую распределения в координатах xi , ni (рис.
6.1).
По результатам построения ломаной кривой можно примерно определить, что самое близкое распределение измеренных параметров изделия - нормальное.
ωр = 6σ; ωр = 0,168 МПа > 0,13 МПа;
ωр > ωф.
7. Строят теоретическую кривую, совместив ее с практической кривой. Для этого используется уравнение:
M H = MЭ CNσ ,
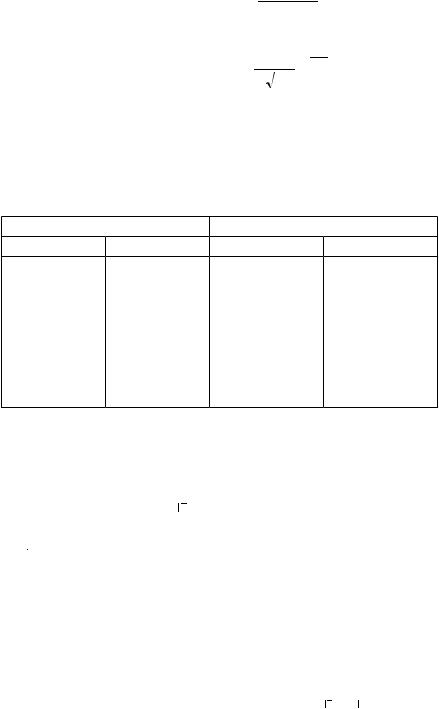
где МН и МЭ - масштабы для кривой нормального распределения и эмпирической кривой;
С - цена разряда принята С = 0,02; N - число деталей в выборке.
MH = 2 × 0,02 ×100 = 143 . 0,028
Воспользовавшись табличными значениями функции
|
|
1 |
e− |
x 2 |
y = |
σ |
2σ 2 , |
||
|
2π |
|
|
получим табл. 6.3.
Таблица 6.3
Вычисление координат точек для построения кривой нормального распределения
Значения x |
|
Значения y |
|
в долях σ |
в мм |
yтабл |
yтабл.МН |
0,0 |
0,00 |
0,399 |
57 |
0,5 |
14,10 |
0,352 |
50 |
1,0 |
28,00 |
0,242 |
35 |
1,5 |
42,00 |
0,130 |
19 |
2,0 |
56,00 |
0,054 |
8 |
2,5 |
70,00 |
0,018 |
3 |
3,0 |
84,00 |
0,044 |
0,5 |
9. Выполняют анализ экспериментальных данных. На рис. 6.2 показано, что кривая распределения смещена относительно центра поля допуска на ω/n:
ω′ |
= |
х |
− |
xc |
р |
= |
0,03 |
МПа, |
|
||||||||
n |
|
|
|
|
|
где xср - середина поля допуска;
х - среднее значение поля размаха;
ω′n - характеризует направление и степень влияния систематических факторов.
Однако при анализе генеральной совокупности нас интересует, как кривая будет вести себя в данном случае, поэтому поле рассеивания параметра определяется зависимостью:
ωn = 2ω′n = 2 |
х − xc р |
. |
|
|
Если, например, ωn = 0,06 МПа,
тогда ω = ωn + ωр = 0,06 + 0,168 = 0,228 МПа,
то есть ω > Т на параметр (0,228 > 0,2). Это значит, что часть параметров изделия в выборке выйдет за пределы допуска.

По форме кривой распределения можно судить о доминирующем закономерно - изменяющемся факторе: двухвершинная кривая при стабильном технологическом процессе указывает на то, что сбилось положение настройки параметра.
По величине ω′n можно судить о качестве настройки параметра при изготовлении изделия.
По соотношению поля рассеивания ωp = 6σ и поля допуска Т можно судить о возможности обеспечение параметра при изготовлении по настройке и допуске на настройку: если ω = ωn + ωp > Т, то возможно появления бракованных изделий.
Следовательно, метод кривых распределения позволяет определить возможный процент годных сборок или деталей.
6.4. Применение статистических методов исследования для оценки точности и настроенности технологических процессов
Заданный уровень качества изделия обеспечивается не только при проектировании конструкции, но и при его изготовлении, ремонте и эксплуатации. В практике после набора статистических данных в случае появления брака по некоторым параметрам технологу приходится разрабатывать мероприятия по обеспечению заданной точности и настроенности технологического процесса. Повышение качества равноценно увеличению объема выпуска, уменьшению затрат труда и материалов.
Рассмотрим решение некоторых часто встречающихся типовых задач при выполнении практических и лабораторных работ.
Задача №1. Требуется определить точность и настроенность процесса обработки, а также возможный процент брака при тонком точении шейки вала
ТНА D = 30js7( |
−0 ,012 |
) мм. Измерения размеров выборки на 50-ти деталях пока- |
||
|
+0 ,012 |
|
|
|
зали, что: средний диаметр - |
D |
= 30,008 мм, оценка среднего отклонения - σ |
||
= 0,005 мм. Предположительно рассеивание размеров подчиняется нормальному закону распределения. По результатам расчетов необходимо предложить пути снижения брака на данной операции.
Последовательность решения подобных задач следующая.
1.Вычисляют допуск на диаметр - Т = 0,024 мм.
2.Определяют поле рассеивания размеров:
ω= 6σ,
ω= 6 . 0,005 = 0,030.
3.Рассчитывают коэффициент точности процесса:
ω
kТ = Т ,

0 ,030 =
kТ = 0 ,024 1,25,
следовательно, процесс неточен.
Коэффициент точности процесса не должен превышать единицы. В некоторых случаях принимают, что kТ не должен превышать 0,8, чтобы создать не-
который запас по размаху текущих параметров. |
|
|
|
||
4. Вычисляют необходимый |
настроечный размер резца (средний |
||||
чертежный размер диаметра) – Dср = 30 мм. |
|
|
|
||
5. Определяют отклонение настройки резца: |
|
||||
|
Тн = Dср - |
D |
, |
|
|
Тн = 30 – 30,008 = - 0,008 |
мм. |
||||
Тогда коэффициент настройки вычисляют по формуле |
|||||
|
|
_ |
σ |
|
|
|
Dcр. |
− D + t |
N |
|
|
|
|
γ |
|
|
, |
k H = |
Т |
|
|
||
|
|
|
|
|
|
где Dcр – средний диаметр вала по чертежу,
tγ - квантиль распределения при уровне значимости γ (приложение 2). При уровне значимости γ = 0,95 и N = 50 квантиль tγ = 2,01. Тогда
kН = 0,41. Но значения kН |
не должно превышать 0,1, поэтому делают |
|||
вывод о том, что настройка процесса выполнена не правильно. |
||||
6. Рассчитывают вероятный процент исправимого и неисправимого брака |
||||
по формулам: |
|
|
|
|
Бнис |
= |
{0,5 + F[(Dнм - |
D )/σ}.100 , |
|
Бис |
= |
{0,5 - F[(Dнб - |
D )/σ}.100 , |
|
где F[(Dнм - D )/σ} и F[(Dнб - |
D )/σ}– функция Лапласа (приложение 3). |
|||
Бнис = {0,5 + F[(29,988 – 30,008)/0,005} .100 =0%,
{0,5 - F[(30.012 – 30,008)/0,005} .100 =21,1%.
Данные расчеты позволяют судить о том, что при изготовлении деталей появился брак, но он исправим. Для уменьшения брака центр группирования
параметров необходимо сместить на величину а = |
D |
- Dcр = 0,008 мм. |
Задача №2. На револьверном станке обработали партию заготовок для форсунок 500 шт. диаметром 20-0,2 мм. По результатам измерения N = 50 пробных заготовок величины среднего и среднего квадратического отклонений составляют d = 19,97 мм и σ = 0,019 мм. Определить число годных и бракованных деталей.
Решение.
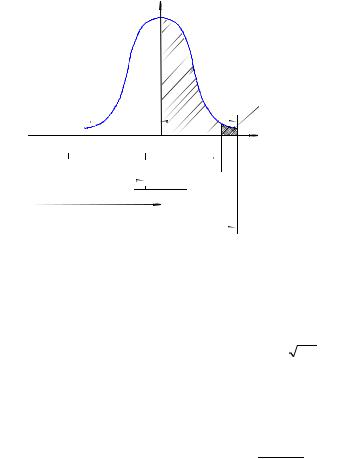
Определяют интервал рассеяния размеров обрабатываемых валов относительно выборочного среднего (в предположении, что их распределение подчиняется закону Гаусса)
ω = ±3 σ = ±3. 0,019 = ±0,057 мм.
Из расположения поля рассеяния фактических размеров заготовок по отношению к полю допуска очевидно, что часть размеров (область размеров F2) будут выходить за допустимый наибольший размер (рис. 1.7).
ó
F1
|
|
|
6.2. Распределение размера 20-0,2 |
|
d ô .í ì |
|
F |
при изготовлении корпуса |
|
- 3σ |
+3σ |
2 |
форсунки |
|
õ |
||||
|
|
|
||
Ò/ 2 |
Ò/ 2 |
|
|
|
dcð |
dñì |
|
|
|
|
|
|
||
d |
|
|
|
|
d ô .í á |
|
|
|
Вся площадь под кривой распределения (полагаем, что она подчиняется закону Гаусса) равна 1, половина ее равна -0,5.
Тогда
|
|
= 0 ,5 − 1 |
z |
− |
Z 2 |
F2 |
= 0 ,5 − F1 |
∫е |
2 dz = 0.5Ф( z ), |
||
|
|
2π |
0 |
|
|
где Ф(z) - функция Лапласа.
Величина z =Т/σ в рассматриваемом случае равна
z = dнб − d ,
σ
= 20 −19,97 =
z  1,58. 0,019
1,58. 0,019
Тогда по приложению 1
Ф(z) = Ф(1,58) = 0,44
и
F2 = 0,5 - Ф(z) ; F2= 0,5 - 0,44 = 0,06,
то есть 6% деталей (18 шт.) будут бракованными, но брак исправим.
Задача 3. По результатам измерения диаметров пяти корпусов агрегата автоматики, обработанных на токарном полуавтомате, сразу после настойки станка и через некоторый промежуток времени получены следующие значе-

ния выборочных средних d 1 = 80 ,01мм и d 2 = 80 ,042 мм , дисперсий σ21 = 0,001 мм2 и σ22 = 0,004 мм2. Определить настоечный размер.
Решение.
1. Сначала проверяют гипотезу о равенстве выборочных дисперсий: σ12 = σ22 по критерию Фишера (приложение 2):
F= σ22 ;
σ12
=0,004 = F  4.
4.
0,001
Так как найденное значение критерия Фишера меньше табличного F = 5,25 при принятом уровне значимости α = 0,05, то гипотеза о равенстве дисперсий принимается. Значит, уровень точности станка не изменился.
2.Вычисляют средневзвешенную дисперсию:
σ2 = (n1 −1)σ12 + (n2 −1)σ 22 ;
+n2 − 2n1
σ 2 |
= (5 −1)0.001 + (5 −1)0.004 = 0.0025мм2 . |
|
|
|
5 + 5 − 2 |
|
|
со степенями свободы |
f = (n1 + n2 − 2); f = 5 + 5 − 2 = 8, , |
|
|
где n1 и n2 – количество заготовок, изготовленных на токарном полуавто- |
|||
мате в разное время. |
|
|
|
Среднее квадратичное отклонение |
σ = σ 2 = 0.0025 = 0.05 |
мм. |
|
3. Проверяют гипотезу о равенстве средних значений |
d1 = d 2 с помощью |
||
критерия Стьюдента. |
|
|
|
Так как |
|
|
|
|
t = d1 − d2 |
; |
|
σ1 + 1
n1 n2
t = 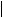 80,01 − 80,042
80,01 − 80,042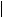 =1,01.
=1,01.
0,05 1 + 1
5 5
Расчетный критерий Стьюдента меньше табличного t = 2,78 (приложение 3), то гипотеза о равенстве средних значений в выборке принимается. Следовательно, настроечный размер за данный промежуток времени не изменился.
Если выборочные дисперсии окажутся неоднородными, значение критерия Стьюдента следует вычислить по формуле:
ϑ1t |
1−α ; f1 |
+ϑ2 t |
1−α ; f 2 |
, |
t = |
2 |
|
2 |
|
|
|
|
||
|
ϑ1 +ϑ2 |
|
|
|
где ϑ1 = σ 12 / n1 и ϑ2 = σ 22 / n2 .
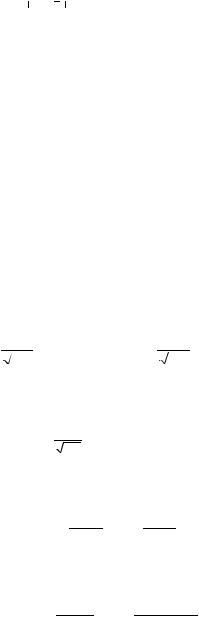
Разницу между средними значениями выборки можно считать значимой (на уровне значимости α), если
|
|
|
|
d1 − d 2 |
>Т. |
|
|
|
Задача №4. Погрешность изготовления отверстия в корпусе ТНА |
||||||||
подчиняются нормальному закону распределения и |
известны: |
допуск на |
||||||
размер |
T |
= -60 мкм, |
среднеквадратическое |
отклонение |
размеров |
|||
σ = 30 мкм, |
интервал варьирования параметров ls = 0, li = -120 мкм. |
|||||||
Определить процент годных деталей. |
|
|
|
|
||||
Расчет следует выполнять в следующей последовательности. |
|
|||||||
Известно, |
что если |
случайная |
величина |
X |
задана |
плотностью |
||
распределения f(x), то вероятность того, что X примет значение, принадлежащее интервалу интервалу (li, ls), такова:
Р(li < X < ls) = |
|
|
ls |
|
|
|
|
|
|
|
||||||
|
|
∫ f ( x )dx |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
li |
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р(li < X < ls) = |
1 |
( ls −T ) / σ |
|
|
|
|
|
- |
1 |
( li −T ) / σ |
|
|
||||
|
∫ e |
− z |
2 / 2 |
dz |
|
|
∫ e |
− z 2 |
/ 2 |
dz. |
||||||
π |
|
|
|
|
π |
|
|
|
||||||||
|
2 |
|
0 |
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
Пользуясь функцией Лапласа (приложение 3) |
|
|||||||||||||||
Ф(х) = |
1 |
х |
|
− z 2 |
|
|
|
|
|
|
|
|
||||
∫ e |
/ 2 |
dz |
|
|
|
|
|
|
||||||||
|
π |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
окончательно получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р(li < X < ls) = |
|
l |
− T |
− |
l |
− T |
|
|
|
|
|
|||||
|
|
|
σ |
|
|
|
|
σ |
|
|
|
|
|
|||
|
|
|
Ф s |
|
|
|
|
Ф i |
. |
|
|
|
|
|
||
Подставляя заданные значения в эту формулу, получим |
||||||||||||||||
Р(-120< X < 0) = |
|
0 + 60 |
− |
|
− 120 + 60 |
= 2Ф( 2 ). |
||||||||||
|
30 |
|
|
|
30 |
|
||||||||||
|
|
Ф |
|
|
|
Ф |
|
|
||||||||
По таблице приложения 1 находим Ф(2) = 0,4772. Отсюда искомая вероятность
Р(-120< X < 0);
Р = 2 . 0,4772 = 0,9544.
Следовательно, при изготовлении корпусов ТНА годных деталей будет
95,44%.
Задача №5. Погрешность обработки наружного диаметра турбины подчиняется закону нормального распределения с Т = -85 мкм и σ = 38 мкм.
Известны: ls = 0, ll = -190 мкм. Определить % брака и величину подналадки, обеспечивающую обработку без неисправимого брака.
По аналогии с предыдущей задачей, подставляя в формулу
